Força, Energia Potencial e Deslocamento
Produzido por Ludovic BeghinTeoria
Introdução
A gente já conhece as forças conservativas mas como calcular o trabalho realizado por elas? A força é chamada de conservativa, pois toda a energia mecânica no sistema se conserva, isso quer dizer que:
Ou seja:
Tá mas onde que entra energia cinética e energia potencial nessa história?
Teorema Trabalho x Energia Potencial
É possível relacionar trabalho com energia potencial e vamos descobrir como. Vamos lembrar que toda a energia mecânica num sistema conservativo se mantém e que a energia mecânica é dada por:
Onde é a energia potencial e a cinética.
E se a variação da energia mecânica é zero a gente pode dizer que:
Como a gente tá tratando de forças, sabemos pelo teorema Trabalho x Energia Cinética que o trabalho de qualquer força é a variação da energia cinética.
Substituindo no que tínhamos:
E enfim temos o teorema Trabalho - Energia Potencial.
Ou seja, o trabalho de uma força conservativa é igual ao inverso da variação da energia potencial associada a essa força.
Vamos entender como funciona isso na prática, qual é o trabalho da força gravitacional em cada caso pra essa bolinha?
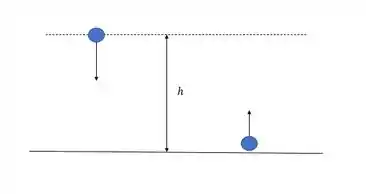
No caso da bolinha descendo o que acontece?
Repara que para a bolinha descendo o trabalho é positivo, e isso faz sentido, afinal tanto a força peso quanto o deslocamento apontam para baixo, na mesma direção. Já no caso da bolinha subindo...
Agora o trabalho é negativo, e isso faz sentido, pois a força peso aponta para baixo, mas o deslocamento aponta para cima!
E no caso desse gráfico de energia potencial? Como calcular o trabalho realizado pela força conservativa entre e ?
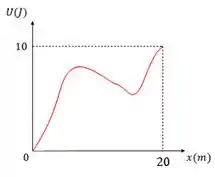
É bem tranquilo!
Sempre lembrando desse sinal que acompanha a fórmula, ok?
Relacionando Energia Potencial e Força
Sabia que a força tem relação com a energia potencial? E aqui falo de qualquer energia potencial, não só a gravitacional. Vamos olhar o teorema trabalho-energia:
Se derivarmos pra
Como:
E se partirmos de uma posição inicial
Lembrando que:
Então:
Beleza, mas como aplicar isso? Temooos muitas aplicações, se liga nesse gráfico de energia potencial com uma equação mostrada:
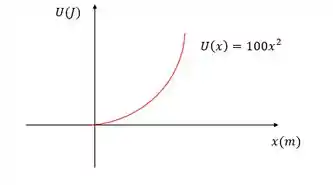
Pra esse gráfico calcular a força relacionada à essa energia, quando a posição
Vamos aplicar a nossa relação com a força:
E substituindo a posição:
Deixa eu te contar um segredo, o que a gente acabou de fazer foi calcular a força elástica que é um tipo de força conservativa que gera energia potencial lembra que:
No geral, quando for calcular a força a partir do potencial, pode ter dois casos:
1) Se te derem a função da energia potencial é só derivar para encontrar a força e substituir o ponto para encontrar a força naquele ponto, como nesse exemplo.
2) Se não te derem a função, aí você vai precisar encontrar a derivada pelo gráfico (nesses casos, geralmente o gráfico é composto por retas que são mais fáceis de fazer a derivada).
Energia Mecânica e Pontos de Retorno
A gente já tá cansado de saber que a energia mecânica do sistema se conserva e isso tem algumas aplicações, uma delas é encontrar os pontos de retorno do gráfico e o que são eles?
A gente já viu que a energia mecânica é composta por:
E que ela é constante, pois a gente tá falando de forças conservativas, então nada sai do sistema, a energia mecânica se transforma de cinética pra potencial e vice-versa.
O ponto de retorno nada mais é do que o ponto onde a energia mecânica é toda energia potencial e com isso a energia cinética é zero.
Olha esse exemplo:
Um esquiador de desce uma montanha e no ponto , a sua velocidade é para a direita, considerando que só há atuação de forças conservativas, mostre no gráfico de potencial abaixo os pontos de retorno desse movimento.
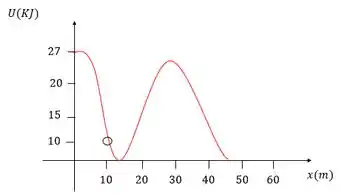
O primeiro passo é calcular a energia cinética no ponto , pois ela somada a energia potencial nesse ponto vai ser a energia mecânica.
Daí fazemos:
E como a energia mecânica é constante ao longo de todo movimento, traçamos uma reta:
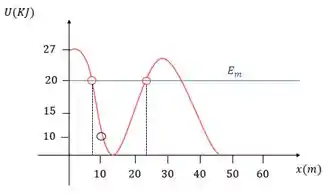
Agora com a reta traçada, temos os nossos pontos de retorno desse movimento:
Isso nos indica que esse movimento do esquiador estará limitado entre esses dois pontos. Lembra que no início, em , ele estava indo para a direita com ?
O esquiador vai continuar indo para a direita até chegar em , quando sua energia cinética é zero e então ele para. Se ele continuar o movimento, terá que ir para a esquerda, e vai chegar em , quando novamente sua energia cinética é zero e ele para. Ou seja, o movimento dele está delimitado entre esses pontos.
O problema pode ficar ainda mais interessante pedindo pra calcular a velocidade em um ponto qualquer do movimento. Imagina que você quer saber a velocidade do esquiador no ponto , como a gente faria isso?
Nesse ponto, olhando para o gráfico, temos que e sabemos que a energia mecânica é constante:
E lembrando que:
Podemos substituir e igualar:
Não podemos esquecer que a unidade deve ser nas contas pra termos a velocidade em .
Terminamos, bora praticar?
Relacionando Energia Potencial e Força
Energia Mecânica e Pontos de Retorno
Exercícios Resolvidos
Exercício Resolvido #1
TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 230 – 8.
A figura mostra o gráfico de uma função energia potencial .
- Para cada ponto indicado, informa se a componente x da força associada a esta função é positiva, negativa ou zero.
- Em que ponto a força tem a maior magnitude?
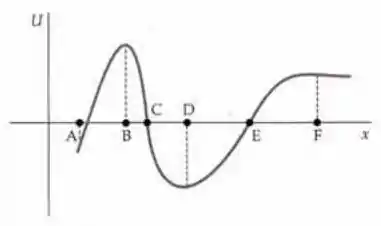
Passo 1
Alternativa a)
Já começo falando pra tu ter atenção ali no ponto A pra ver onde ele ta direitinho, porque ele não está em cima do eixo x!
Agora voltando pra analisar, vamos usar essa paradinha aqui ó
Como o gráfico é justamente o gráfico do potencial, vamos analisar só a derivada, se a derivada for positiva a força é negativa, se a derivada for negativa a força é positiva.
Passo 2
Como a derivada no ponto é positiva, a força é negativa!
Como a derivada no ponto é zero, a força é nula!
Como a derivada no ponto é negativa, a força é positiva!
Como a derivada no ponto é zero, a força é nula!
Como a derivada no ponto é positiva, a força é negativa!
Como a derivada no ponto é zero, a força é nula!
Quadro resuminho:
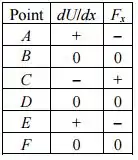
Passo 3
Alternativa b)
Agora temos que encontrar em que ponta a força tem maior magnitude. O que isso quer dizer?
Que temos que achar o ponto que apresenta a menor derivada! Se analisarmos no gráfico, esse será o ponto C.
Resposta
a)
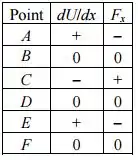
b) O ponto C.
Exercício Resolvido #2
TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 231 – 28.
A energia potencial de um corpo restrito ao eixo é dada por , onde está em joules e está em metros. Determine a força associada a esta função energia potencial.
Passo 1
Bom, vamos ter que usar umas derivadas aqui, mas derivada de polinômio é algo tranquilo pra gente, sacou? Vou te lembrar como faz !!!
Sabemos que a relação da força com o potencial é a seguinte expressão:
Passo 2
Pra saber como a força varia de acordo com o potencial, vamos derivar a expressão que foi dada no enunciado:
Lembrando que pra derivar polinômio, a gente tira 1 do expoente e multiplica pelo antigo expoente, tipo isso aqui:
Derivando a expressão que ele deu pra gente ficamos com:

Resposta
Exercício Resolvido #3
TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 231 – 27.
A força sobre um corpo é dada por . Em , sabe-se que a força aponta no sentido e tem a magnitude de . Determine a energia potencial associada a esta força como função de , atribuindo um valor de referência de em para a energia potencial.
Passo 1
Bom, mais uma vez vamos usar a única fórmula que a gente sabe que relaciona a força e a energia potencial, hahahaha
Mas pra saber a energia potencial, vamos precisar saber primeiro a força
Passo 2
Vamos ver o que o enunciado deu pra gente:
Assim, é só substituir os valores que a gente consegue achar o valor de .
Passo 3
Agora que já sabemos , vamos integrar

Calma, a integral é simples, hahahahaha
Passo 4
Agora a gente precisa saber quanto vale aquele ali. Se lembra que ele deu um valor de pra gente? Vamos usar ele agora!
Gostou da resolução ??????

Resposta
Exercício Resolvido #4
UFRJ-Física 1-Prova 1-2012.1 Múltipla Escolha n°7.
Uma única força conservativa atua em uma partícula paralela ao eixo horizontal de um sistema de coordenadas. A energia potencial desta força é dada pela figura abaixo. Qual opção representa corretamente os vetores (direção, intensidade e sentido) das forças que atuam sobre a partícula nos pontos e respectivamente.
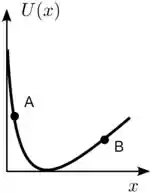
![]()
- diagrama 4
- diagrama 1
- diagrama 5
- diagrama 2
- diagrama 3
Passo 1
Lembra que no gráfico de energia pela posição
- Força positiva: Quando o gráfico for decrescente a força será positiva.
- Força negativa: Quando o gráfico for crescente a força será negativa
Passo 2
Então
Porém temos dois diagramas que falam isso, o e o . Um detalhe importante é entendermos a intensidade da força.
É um pequeno detalhe, mas quanto mais “rápido” ele está variando, maior vai ser o seu módulo. O ponto está em uma descida muito mais “forte” que a subida do ponto. Então
Resposta
Letra E