Equilíbrios e Energia Potencial
Produzido por Ludovic BeghinTeoria
Gráficos de Energia Potencial e suas Forças
Acabamos de ver que a energia potencial sempre está associada a uma força. Ao observar um gráfico de energia potencial por posição podemos determinar alguns detalhes das forças.
Porém, antes de entender isso devemos rever equilíbrio. Diferente do que se imagina, existem tipos de equilíbrio que precisamos saber,
- Estável: É quando um objeto, que está em equilíbrio, se move, mas logo em seguida ele volta a posição de equilíbrio.
- Instável: É quando um objeto, que está em equilíbrio, se move e, logo em seguida, sai do equilíbrio.
- Indiferente: É quando, independente das forças, o objeto continua sempre em equilíbrio. Se você empurrar a sua cama, ela não vai fica se mexendo, ela simplesmente fica parada quando você parar de empurrar, isso é o equilíbrio indiferente.
Um exemplo disso é a suspensão de um carro. Se você empurrar o capô do seu carro depois de um tempo ele para de balançar e volta a ficar parado, ou seja, ele voltou para o equilíbrio.
Um exemplo disso é quando você tem aquela garrafa de água vazia em cima da mesa, quando bate um vento a garrafa balança e de repente cai. Isso é o mesmo que falar que ela estava em equilíbrio e o vento fez com que ela perdesse esse equilíbrio e não conseguisse recuperar.
Trabalhando com gráficos e os tipos de Equilíbrio
Tendo visto isso, vamos aprender a interpretar o gráfico de Energia potencial pela posição.
Vamos analisar o gráfico abaixo.

Temos duas coisas que podemos determinar pelo gráfico
- Sinal da força: Temos que olhar quando o gráfico é crescente ou decrescente
- Força positiva: Quando o gráfico for decrescente a força será positiva.
- Força negativa: Quando o gráfico for crescente a força será negativa.
- Equilíbrio Estável: Acontece quando a função estiver no mínimo local, que é a parte baixa das “voltinhas”.
- Equilíbrio Instável: Acontece quando a função estiver no máximo local, que é a parte alta das “voltinhas”, isso acontece porque quando você se move para a direita a força passa a ser positiva e quando você se move para a esquerda a força é passa a ser negativa. Esses dois sentidos da força fazem o objeto sair do seu ponto de equilíbrio e se distanciar dele cada vez mais.
- Momento
- Momento B
Isso acontece porque quando você se move para a direita a força passa a ser negativa e quando você se move para a esquerda a força passa a ser positiva.
Esses dois sentidos da força fazem o objeto voltar ao seu ponto de equilíbrio já que são em sentido oposto ao movimento.
No gráfico acima a análise fica

Quer ver um jeito bem tranquilo se pensar em estável e instável? Quando eu vi pela primeira vez, usava muito esse macetinho. Se liga nesses carrinhos:

Vamos analisar o carrinho nos momentos e , fechado?
Pensa assim: se você empurrar ele pra frente e largar, ele cai, né? Se você empurrar ele pra trás e largar, ele também cai, né? Qualquer toquezinho que você de no carrinho ali, ele vai cair, tanto pra tras ou pra frente, ou seja, naquele ponto, o equilíbrio dele é instável!
Agora nesse carrinho vai ser diferente: se você empurrar ele e largar, tanto pra frente ou pra trás, a tendência dele é voltar pro mesmo lugar, ou seja, aqui vamos ter um equilibro estável!
Trabalhando com gráficos e os tipos de Equilíbrio
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ-Física 1-Prova 1 - 2012.2 Múltipla Escolha n°3.
Uma partícula desloca-se ao longo do eixo sob a ação de uma força conservativa , correspondente a um potencial , dado pela figura abaixo. Para este potencial entre as opções abaixo a única incorreta é:
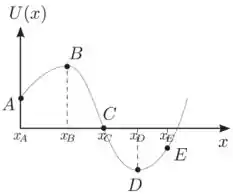
- Na posição a força sobre a partícula é nula;
- Na posição , tem-se a condição de equilíbrio estável;
- No deslocamento do corpo de para o trabalho realizado pela força é positivo;
- O sentido da força na posição é negativo;
- Na posição a força é nula.
Passo 1
Vamos analisar cada item
a)
Verdadeiro, Em B temos um máximo, a “voltinha” está virada para cima então a força nesse ponto é zero
Passo 2
b)
Verdadeiro, Em D temos um mínimo, a “voltinha” está virada para baixo, então temos equilíbrio estável, como vimos na teoria.
Passo 3
c)
Verdadeiro, Podemos relacionar o trabalho da força com sua variação de energia potencial
Pelo gráfico
Então
E
Passo 4
d)
Verdadeiro, em o gráfico é crescente, que nos diz q a força é negativa
Passo 5
e)
Falso, a força só é zero quando temo um máximo ou um mínimo.
Resposta
Letra E
Exercício Resolvido #2
UFRJ-Física 1-Prova 1-2014.1 Múltipla Escolha n°4
Uma partícula desloca-se ao longo do eixo , de unitario , sob ação de uma força conservativa , correspondente ao potencial , dado pelo gráfico da figura. Para este potencial, entre as alternativas abaixo, a única INCORRETA é
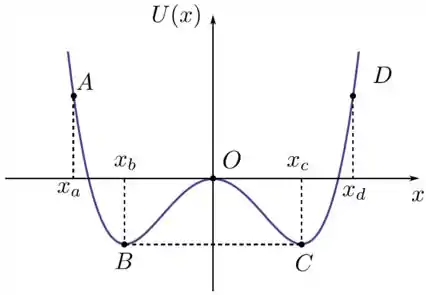
- Na posição a força sobre a particula é nula;
- Nas posições e tem-se a condição de equilíbrio estável;
- No deslocamento da particular de para o trabalho realizado pela força é negativo;
- No deslocamento da partícula de para a variação da energia cinética é ;
- Na posição o sentido da força é positivo.
Passo 1
Vamos analisar cada item
a)
Verdadeiro, temos um máximo em O, dessa forma a força é zero
Passo 2
b)
Verdadeiro, ambos os pontos são pontos de mínimo , eles têm a "voltinha" virada para baixo, então eles estão em equilíbrio estável
Passo 3
c)
Verdadeiro, Podemos relacionar o trabalho da força com sua variação de energia potencial
Pelo gráfico
Então
E
Passo 4
d)
Falso, a energia mecânica se conserva porque, temos apenas.uma força conservativa.
Como a energia potencial em B é igual à energia potencial em C temos
Então
Passo 5
e)
Verdadeiro, como a função é decrescente em A a força é positiva.
Resposta
Letra D
Exercício Resolvido #3
USP-Física I-Prova 2-2014- Questão 1
Uma partícula de massa pode se deslocar em uma dimensão, submetida a um potencial dado por em unidades do SI: em Joules (), e em metros ().
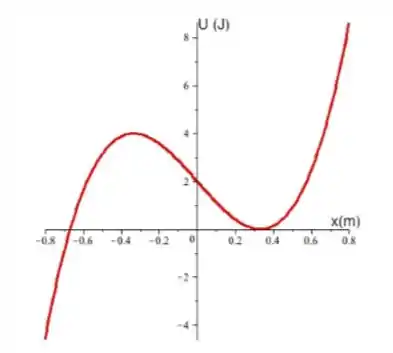
Determine a expressão da força atuando sobre a partícula em função da posição .
Calcule as posições de equilíbrio da partícula.
Determine as condições de equilíbrio em cada ponto, ou seja, se é estável, instável ou indiferente.
Se uma partícula de massa for deixada na condição de equilíbrio estável com velocidade de , ela realiza um movimento periódico? Justifique.
Passo 1
Utilizando a relação:
Passo 2
As posições de equilíbrio ocorrem onde a derivada é zero, logo:
Resolvendo a equação do segundo grau temos duas soluções:
Passo 3
Basta observar o gráfico e ver o que acontece antes e depois do ponto de equilíbrio.
No ponto temos um ponto de máximo, ou seja, a função decresce antes e depois do ponto. Logo, é um ponto de equilíbrio instável.
No ponto temos um ponto de mínimo, ou seja, a função cresce antes e depois do ponto. Logo, é um ponto de equilíbrio estável.
Passo 4
O ponto é o ponto de equilíbrio, neste ponto, a energia potencial é zero segundo o gráfico. Logo a energia mecânica se dará apenas pela energia cinética:
Agora vamos analisar o gráfico, ao lado direito do ponto o gráfico cresce infinitamente, logo a partícula irá alcançar determinada energia e voltar ao ponto de equilíbrio. Entretanto, no lado esquerdo ao ponto o gráfico possui um ponto de máximo em que ele volta a decrescer depois. Esse ponto, segundo o gráfico possui energia potencial de , que é menor que , logo a partícula será capaz de passar por esse ponto e depois decrescer infinitamente, não retornando mais ao ponto .
Portanto, o movimento não será periódico.
Resposta
O ponto é um ponto de equilíbrio instável.
O ponto é um ponto de equilíbrio estável.
O movimento não será periódico.
Exercício Resolvido #4
USP-Física I- PREC- 2013- Questão 1.
A energia potencial de ligação entre átomos de moléculas diatômicas pode ser descrita, dentro de certos limites, pelo gráfico ao lado, dado pela equação
onde é a distância entre os núcleos dos átomos, a e b são constantes. 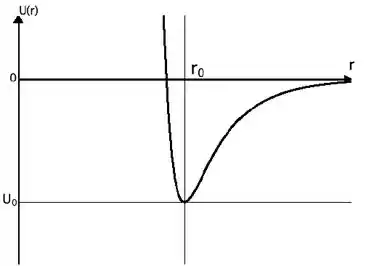
a) Qual a equação da força entre os átomos?
b) Determine a distância de equilíbrio .
c) Determine a energia potencial mínima .
Dê suas respostas somente em termos de e .
Passo 1
a)
Ah, parece ser bem hard mas é bem simples de resolver.
Sabemos que a força pode ser calculada por:
Derivando a nossa função, teremos:
Passo 2
b)
Pelo gráfico, vemos que o ponto de equilíbrio é dado justamente no ponto em que o gráfico é horizontal, ou seja, a derivada é nula .
Daí, teremos:
Passo 3
c)
Já que a gente sabe o ponto em que o potencial é mínimo, agora é só calcular o potencial nesse ponto.

Resposta
b)
c)