Teorema Trabalho-Energia Cinética
Produzido por Ludovic BeghinTeoria
O Teorema Trabalho-Energia Cinética diz que o trabalho realizado pela força resultante que atua em um corpo é igual a variação da sua energia cinética. Ou seja:
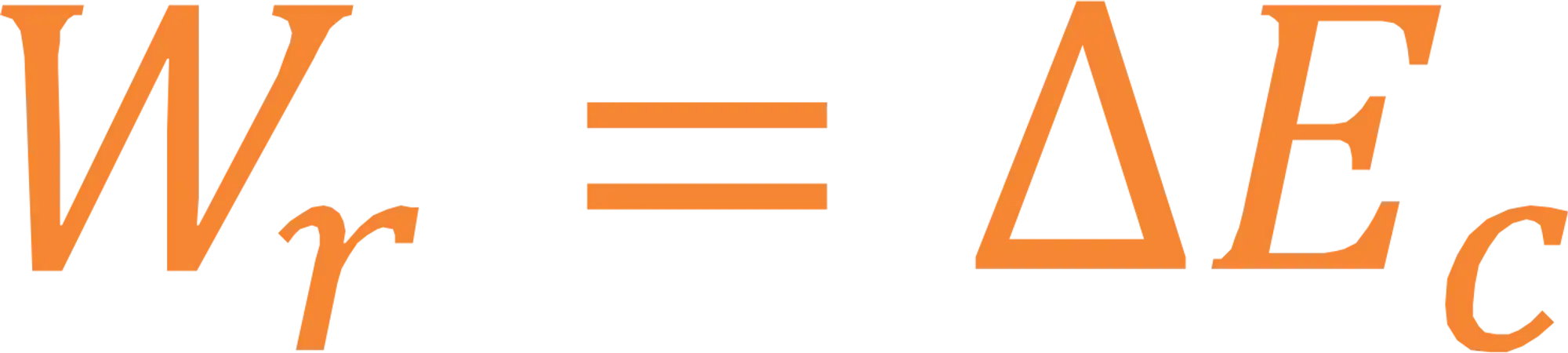
Onde
É importante ter em mente que o trabalho da força resultante é a soma dos trabalhos realizados por todas as forças que estão atuando no sistema, ou seja, se a força está fazendo trabalho ela tem que estar dentro dessa continha ai!
📢 Clique para ver mais:
- Teorema Trabalho-Energia Cinética: Exercícios Resolvidos
- Trabalho Realizado Pela Força Gravitacional
- Conservação da Energia Mecânica
Quer saber como resolver problemas envolvendo o teorema trabalho-energia cinética?! Então se liga nesse vídeo completaço que o Responde Aí preparou pra você! 👇👇👇
Exemplo: Demonstre o Cálculo da Energia Cinética do Bloco Abaixo
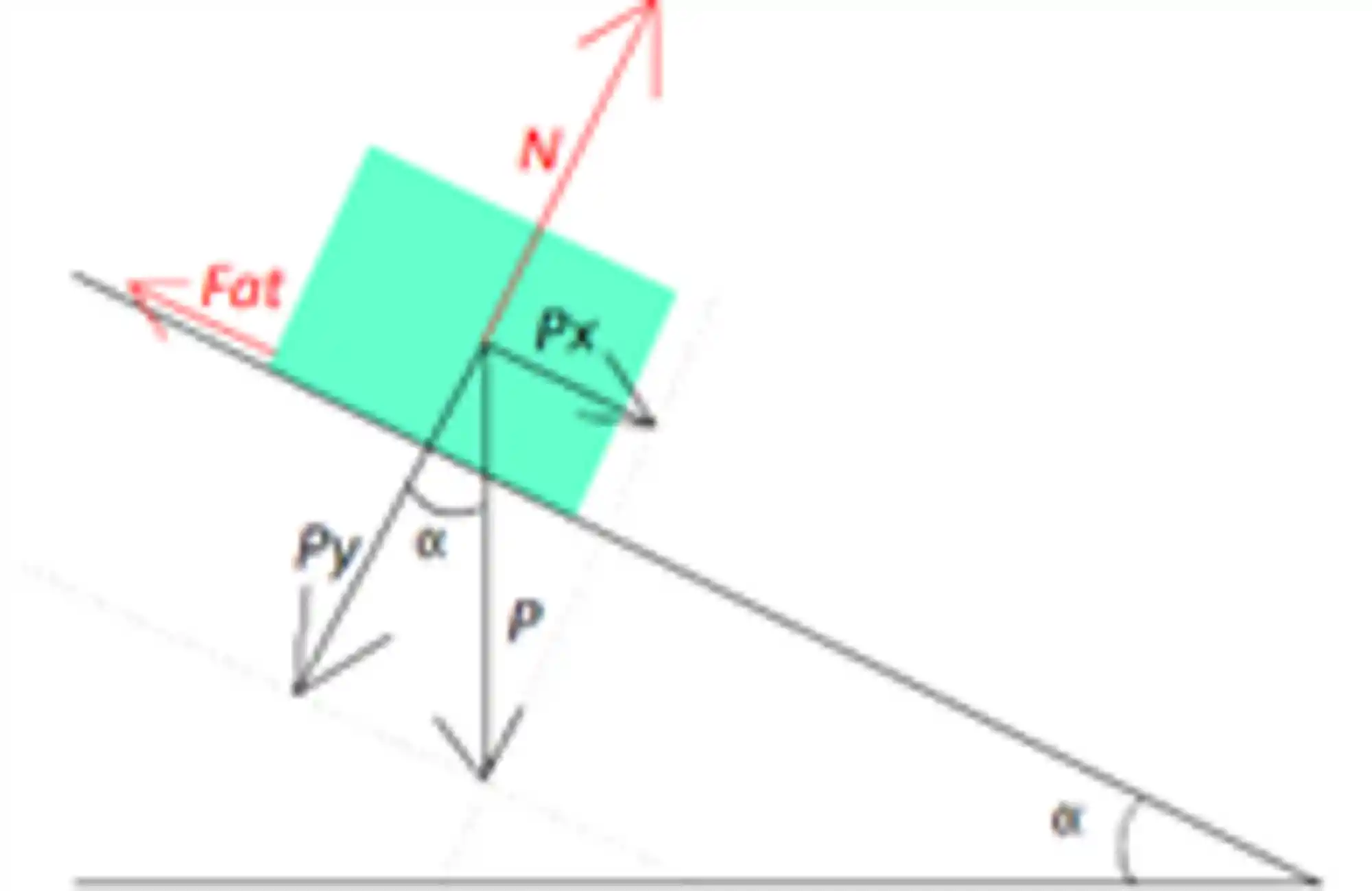
Nessa figura nós temos três forças atuando no bloquinho:
Onde
É sempre bom ficar atento aos sinais dos trabalhos. Como o bloco vai descer, já da pra perceber que o trabalho da força peso é positivo, trabalho da é negativo e o trabalho da força normal é zero pois a força é perpendicular ao deslocamento!
Assim a gente consegue descobrir a energia cinética que o bloco vai ter após a realização dos trabalhos:
Agora vamos praticar com exercícios?!
Exemplo: Demonstre o Cálculo da Energia Cinética do Bloco Abaixo
Exercícios Resolvidos
Exercício Resolvido #1
TIPLER, Física, Vol 1,6ª Edição, LTC,2009., pp 191 – ex24
Uma caixa de é levantada de uma altura de , a partir do repouso, por uma força aplicada vertical de . Encontre a energia cinética final da caixa.
Passo 1
Bom, vamos usar o teorema trabalho-energia cinética. Tem dois trabalhos sendo realizados aqui: o da força e o da gravidade. Vamos calcular os dois.

Passo 2
Calculando o trabalho realizado pela força aplicada:
Passo 3
Calculando o trabalho realizado pela força gravitacional:
Como ele vai da altura até a altura :
Passo 4
Agora vamos aplicar o teorema né?
Como a caixa partiu do repouso, ele não possuía energia cinética nenhuma.
Como a energia cinética inicial da caixa era nula, temos que a energia cinética final é:
Resposta
Exercício Resolvido #2
Elaboração Própria
Uma bomba de um prédio é usada para levar a água encanada da rua, até a caixa d’água localizada no telhado do prédio. A diferença de altura que a bomba deve vencer é , a bomba tem uma vazão de , e a velocidade com que a água chega à caixa d’água é . Desprezando as perdas de energia, determine o trabalho que a bomba realiza em uma hora de operação.
Passo 1
Pelo enunciado teremos que
Como ele quer a o trabalho realizado por uma hora podemos achar a massa de água que sofre esse trabalho
Passo 2
Como existe variação de velocidade vamos usar o teorema trabalho energia
Existem duas forças atuando no sistema, a força peso e a força da bomba
Repare que o trabalho da força peso é negativo porque a água está subindo enquanto a força peso está apontada para baixo, ou seja, a força tem sentido contrario ao deslocamento.
Passo 3
Além disso
Passo 4
Usando o teorema trabalho energia cinética
Resposta
Exercício Resolvido #3
PUCRIO-Física I-Prova 2-2013.2-Questão n°1
Um corpo de massa move-se apenas sobre o eixo . Na origem, sua velocidade vale , e o gráfico a seguir mostra a variação da força resultante que atua sobre o corpo.
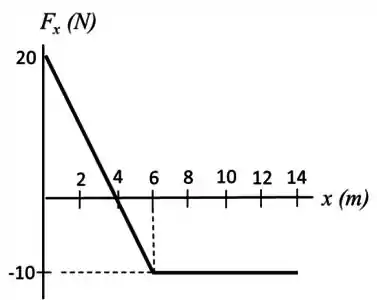
Qual a energia cinética do corpo, e qual a sua velocidade em ?
Responda, justificando, para que valor de a energia cinética do corpo é máxima? Quanto vale sua velocidade aí?
Para qual (ou quais) valor(es) de a velocidade instantânea do corpo vale ?
Passo 1
Quando temos um gráfico de força por deslocamento, devemos sempre lembrar que a área abaixo da curva é igual ao trabalho!
Para calcular a energia cinética em , precisamos utilizar o teorema do trabalho e energia cinética, ele nos diz:
Passo 2
Para calcular o trabalho, precisamos calcular a área abaixo da curva entre e :
Teremos o triângulo, entre e :
E o trapézio entre e :
O trabalho será então:
Lembrando que curvas abaixo do eixo, como , contribuem negativamente!
Passo 3
Voltando à equação da variação de energia, temos:
Onde é a energia cinética do corpo em . Substituindo os valores conhecidos, temos:
Agora que temos a energia cinética, determinar a velocidade é fácil, se liga!
Substituindo os valores, temos:
Passo 4
Pelo teorema do trabalho e energia cinética, podemos ver que a variação da energia cinética será positiva, ou seja ela irá aumentar até quando o trabalho for positivo. Desse modo, podemos ver pelo gráfico que isso ocorrerá até , que é onde o trabalho passa de positivo para negativo.
Já calculamos, no item , o trabalho realizado de 4, ele vale . Pelo teorema, temos:
Substituindo os valores, temos:
Passo 5
Para determinar os valores de em que a velocidade instantânea é vamos utilizar o mesmo teorema, só que agora faremos um caminho um pouco diferente. Temos a velocidade, ou seja, podemos calcular a variação da energia cinética. E com isso encontraremos para que valor de trabalho temos essa variação. Se liga!
Substituindo os valores conhecidos, temos:
Ou seja, os pontos em que a velocidade instantânea é , são aqueles em que o trabalho é .
Passo 6
Sabemos que existe um ponto desses entre e , pois em , o trabalho vale Utilizaremos novamente a área, sabendo que seu valor deve ser .
Para qualquer valor antes de , a área abaixo da curva será a de um trapézio. Para achar o valor de , precisamos determinar e quação da curva, pois somente dessa maneira teremos a base menor do trapézio, se liga!
Para determinar a equação da curva, é só substituir dois ponto, desse modo, acharemos:
A área do trapézio será dada por:
Igualando a , temos:
Acharemos como solução dessa equação, os valores:
Desses valores, somente é válido, pois depois de , o comportamento da curva muda.
Passo 7
Vamos agora analisar a existência de um ponto onde o trabalho seja depois de . Sabemos que a partir de , o comportamento da curva muda, em , temos que o trabalho é:
Depois de , a área será dada por um retângulo, precisamos então, achar para que valor de , a área desse retângulo será igual a , pois !
Igualando a , temos:
Pronto, temos que a velocidade instantânea do corpo será igual a para os eguintes valores de :
Resposta
;
;