Exercícios de Teorema Trabalho-Energia Cinética - Lista de Exercícios Resolvida
Questão 1
Uma caixa de é levantada de uma altura de , a partir do repouso, por uma força aplicada vertical de . Encontre a energia cinética final da caixa.
Ver solução completaQuestão 2
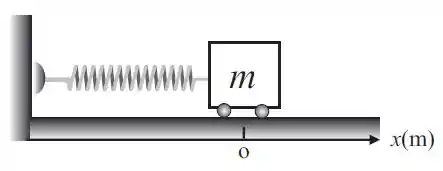
Um corpo de massa move-se apenas sobre o eixo . Na origem, sua velocidade vale , e o gráfico a seguir mostra a variação da força resultante que atua sobre o corpo.
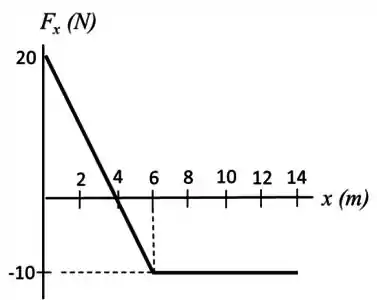
Qual a energia cinética do corpo, e qual a sua velocidade em ?
Responda, justificando, para que valor de a energia cinética do corpo é máxima? Quanto vale sua velocidade aí?
Para qual (ou quais) valor(es) de a velocidade instantânea do corpo vale ?
Ver solução completaQuestão 3
Uma bomba de um prédio é usada para levar a água encanada da rua, até a caixa d’água localizada no telhado do prédio. A diferença de altura que a bomba deve vencer é , a bomba tem uma vazão de , e a velocidade com que a água chega à caixa d’água é . Desprezando as perdas de energia, determine o trabalho que a bomba realiza em uma hora de operação.
Ver solução completaQuestão 4
Um corpo de dimensões desprezíveis e de massa é liberado a partir do repouso da borda de um poço semiesférico de raio . Ele desliza pela parede do poço e após algumas oscilações em torno do fundo do poço permanece em repouso nesta posição. Para as forças presentes desde o inicio até o fim do movimento do corpo é correta a opção
- O trabalho da força peso é ;
- O trabalho da força normal que a superfície do poço exerce sobre o corpo não é nulo;
- O trabalho total das forças dissipativas é nulo;
- O trabalho total das forças dissipativas é ;
- O trabalho total das forças dissipativas é ;
Questão 5
Uma partícula se desloca ao longo do eixo , da origem até a posição , onde é uma distância positiva. A única componente da força resultante sobre a partícula, , varia com a posição conforme o gráfico da figura, linearmete da origem a , cortando o eixo em , e também linearmente de até ; no gráfico também está indicado o valor máximo da força. Denotando por , , e as energias cinéticas nas posições , , e , respectivamente, podemos afirmar sobre as variações , e que
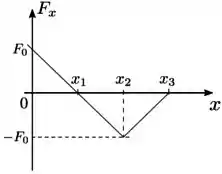
- e
Questão 6
A figura mostra um sistema formado por um bloco (ou uma partícula) de massa e uma mola de constante elástica e comprimento de equilíbrio , ambos sob um plano inclinado que forma um ângulo com a horizontal. O bloco, que não está conectado à mola, está inicialmente no ponto e comprime a mola de uma distância . No instante inicial , o bloco é liberado e se movimenta ao longo do plano inclinado e da base plana . Há atrito apenas no trecho (coeficiente de atrito cinético e estático ), a aceleração da gravidade é e o bloco permanece em contato com a superfície durante o movimento .
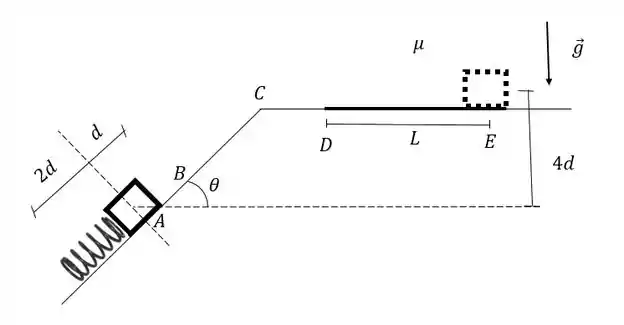
a) Indique esquematicamente na figura abaixo as forças que atuam no bloco no instante inicial

b) Determine o módulo da velocidade do bloco no ponto
c) Determine o módulo da velocidade do bloco no ponto
d) Dado que o bloco entra em repouso no ponto , calcule o coeficiente de atrito do trecho DE em termos de e .
Ver solução completaQuestão 7
Um carro de sobe uma estrada inclinada de por uma distância de e depois desce por outra estrada inclinada de por uma distância de . Se a velocidade no início da subida era de e o trabalho do atrito da roda e do ar sobre o carro durante a subida e a descida foi de, diga qual é o valor do modulo da velocidade do carro no final da descida.

Questão 8
Uma partícula desloca-se em um determinado trajeto e sua velocidade em função do tempo é descrita de acordo com o gráfico apresentado na figura. Considere os instantes , e . Os trabalhos realizados pela força resultante sobre a partícula entre e , , e entre e , , são dados por
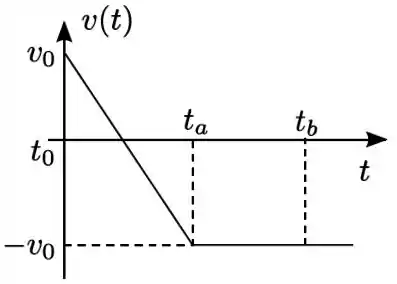
(a) e
(b) e
(c) e
(d) e
(e) e
Ver solução completaQuestão 9
Um corpo de massa move-se apenas sobre o eixo . Na origem, sua velocidade vale , e o gráfico a seguir mostra a variação da força resultante que atua sobre o corpo.
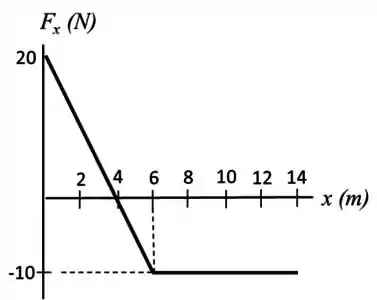
Qual a energia cinética do corpo, e qual a sua velocidade em ?
Responda, justificando, para que valor de a energia cinética do corpo é máxima? Quanto vale sua velocidade aí?
Para qual (ou quais) valor(es) de a velocidade instantânea do corpo vale ?
Ver solução completaQuestão 10
Uma moeda de massa m está sobre uma estrutura de concreto em forma de U, e começa a escorregar por um dos lados. Depois de oscilar algumas vezes, a moeda para na parte mais baixa. Qual o trabalho realizado pela força de atrito? Considere que a estrutura de concreto tem altura H e largura L.
- .
Questão 11
Dois objetos, de massa e , estão se movendo para a direita com a mesma energia cinética. A mesma força constante para a esquerda é aplicada às duas massas. Se , a razão entre a distância que leva para parar e a distância que leva para parar é
- 1.
Questão 12
Um bloco de é mantido contra uma mola de massa desprezível cuja constante elástica é e que sofre uma compressão de . O bloco é liberado do repouso no ponto A e a mola projeta o bloco por um plano inclinado ascendente cujo ângulo com a horizontal é . O bloco atinge o repouso momentâneo no ponto B. Desprezam-se as forças de atrito. Admita que o bloco perca contato com a mola quando esta está relaxada.
- Faça um diagrama das forças atuando no bloco em algum momento antes de se desprender da mola.
- Utilizando o teorema do trabalho-energia, qual a distância, ao longo do plano inclinado, entre o ponto A e o ponto B?
- Quando o bloco desliza de volta para baixo, qual é a sua velocidade no ponto médio do caminho entre A e B? (Dado: utilize se necessário)
Questão 13
Uma bola de é liberada a partir do repouso acima da superfície da Terra. Durante a queda, a energia térmica total da bola e do ar aumenta de . A velocidade da bola pouco antes de atingir a superfície é:
- .
Questão 14
Um bloco de massa repousa sobre uma mesa de altura , e comprime uma mola de constante contra a parede. No instante inicial o bloco está em repouso a uma distância da extremidade da mesa, e a compressão da mola é igual a (em relação à sua posição de equilíbrio). O bloco é então liberado, desliza até a extremidade da mesa e cai no chão (vide figura). O coeficiente de atrito cinético entre o bloco e a mesa é .
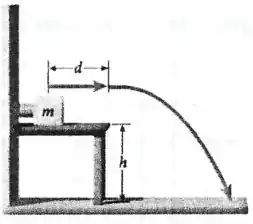
a) Faça o diagrama das forças para o bloco quando o mesmo desliza sobre a mesa, antes de perder o contato com a mola; e durante a queda.
b) Qual é o trabalho realizado pela força de atrito?
c) Qual é o módulo da velocidade com que o bloco chega ao chão?
d) Qual seria o módulo da velocidade com que o bloco chegaria ao chão se não houvesse atrito entre o bloco e a mesa?
Ver solução completaQuestão 15
Em um posto para carga de caminhões do correio, um pacote de é largado do repouso no ponto sobre um trilho com a forma de um quarto de circunferência de raio e desliza até o ponto sem atrito (vide figura). Depois do ponto ele desliza por uma distância de sobre uma superfície horizontal com atrito até parar no ponto . As dimensões do pacote são desprezíveis, de modo que ele pode ser considerado um ponto material.
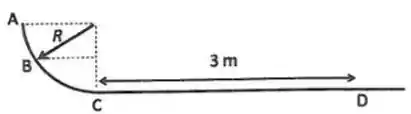
- Qual é a força normal no ponto que fica a uma altura igual a da base do trilho?(Indique a direção e o sentido da normal na figura.)
- Qual é o trabalho realizado pela força normal de até ?
- Qual é o trabalho realizado pela força de atrito?
- Qual é o coeficiente de atrito cinético entre o pacote e a superfície horizontal?
Questão 16
Um bloco de massa está pendurado, através de um fio leve que passa por uma polia sem massa e sem atrito, a um segundo bloco, também de massa . O coeficiente de atrito cinético entre o bloco e a mesa é 0,40. O bloco sobre a mesa é empurrado contra a mola, comprimindo-a de a partir de sua posição relaxada. A mola tem uma constante elástica de .
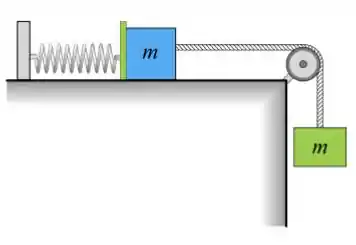
a) Mostre o diagrama das forças que atuam em ambos os blocos imediatamente após o bloco sobre a mesa ser solto.
b) Calcule o trabalho da força de atrito no bloco sobre a mesa até que a mola volte à sua posição relaxada
c) Calcule o trabalho da força peso do bloco pendurado enquanto a mola volta à sua posição relaxada;
d) Calcule a velocidade dos dois blocos no instante em que o bloco pendurado desceu .
Ver solução completaQuestão 17
Um bloco de massa está acoplado a uma mola de constante elástica sobre uma plataforma horizontal, não havendo atrito entre a plataforma e o bloco. A plataforma se encontra inicialmente sendo sustentada a uma altura em relação ao solo e o bloco estirado de em relação ao ponto de equilíbrio da mola (ver figura).
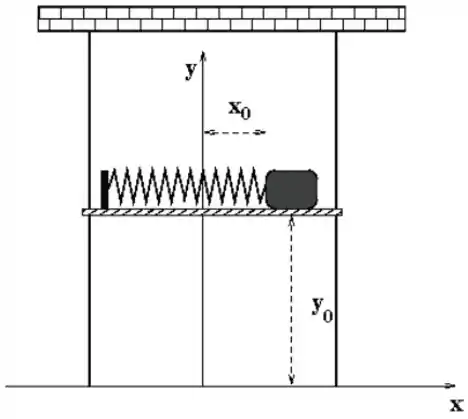
Nesta configuração, simultaneamente a plataforma é solta e começa a cair livremente (escorregando pelas hastes sem atrito) e o bloco é solto.
Sendo assim, havendo saído do repouso, o bloco tem dois movimentos: oscila horizontalmente, enquanto cai em queda livre.
Tome a posição de equilíbrio da mola e a posição no solo (tal como no sistema de referência da figura), e .
a) Calcule o trabalho total sobre o bloco, devido às forças da mola e da gravidade, desde o ponto de partida até atingir uma altura e uma posição horizontal .
b) Justifique claramente porquê as forças envolvidas neste movimento são conservativas.
c) Encontre a velocidade escalar do bloco, , em função de uma altura genérica e posição horizontal . Justifique cuidadosamente os passos para chegar a esta expressão.
d) Observa-se que o bloco tem a mesma velocidade escalar quando está em dois pontos distintos: e . Sabendo que o bloco tem massa , encontre a constante elástica da mola.
Ver solução completaQuestão 18
Uma caixa desliza sobre uma superfície horizontal com velocidade escalar de quando, no ponto , encontra uma área áspera. Na área áspera, o coeficiente de atrito não é constante, mas se inicia a em e aumenta linearmente conforme ultrapassa , atingindo um valor de a após o ponto .
a) Use o teorema do trabalho-energia cinética para achar a distância percorrida por essa caixa antes de parar.
Ver solução completaQuestão 19
Um objeto de massa é largado do repouso de um prédio a uma altura em relação ao solo. Uma mola ideal foi colocada no solo para suavizar a desaceleração do objeto. Esta mola possui uma constante elástica e um comprimento quando não está deformada. Dado: .
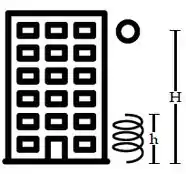
(a) Determine o trabalho realizado pela força peso até o instante de contato entre o objeto e a mola.
(b) Desprezando a resistência do ar, qual deve ser a constante elástica da mola para que o objeto pare momentaneamente a uma altura em relação ao solo?
(c) Considerando agora o efeito da resistência do ar durante a queda, observa-se que o objeto inicia o contato com a mola a uma velocidade . Qual é o trabalho realizado pela força de resistência do ar durante a queda até o instante em que o objeto inicia o contato com a mola?
Ver solução completaQuestão 20
Um próton com massa igual a é impulsionado com uma velocidade inicial de diretamente contra um núcleo de urânio situado a uma distância de . O próton é repelido pelo núcleo de urânio com uma força de módulo , onde é a distância entre as duas partículas e . Suponha que o núcleo de urânio permaneça em repouso.
a) Qual é a velocidade do próton quando ele está a uma distância de do núcleo de urânio?
Ver solução completaQuestão 21
Um próton com massa igual a é impulsionado com uma velocidade inicial de diretamente contra um núcleo de urânio situado a uma distância de . O próton é repelido pelo núcleo de urânio com uma força de módulo , onde é a distância entre as duas partículas e . Suponha que o núcleo de urânio permaneça em repouso.
b) À medida que o próton se aproxima do núcleo de urânio, a força de repulsão faz sua velocidade diminuir até ele ficar momentaneamente em repouso, depois passando a se afastar do núcleo de urânio. Qual é a distância mínima entre o próton e o núcleo de urânio?
Ver solução completaQuestão 22
Um professor de física está sentado em sua cadeira, que desliza sobre rolamentos sem atrito, sendo empurrado para cima de um plano inclinado a acima da horizontal. A massa total do professor com sua cadeira é igual a . Ele é empurrado ao longo do plano inclinado por um grupo de alunos que juntos exercem uma força horizontal constante de . O professor possuía uma velocidade de na base da rampa. Use o teorema do trabalho-energia cinética para calcular sua velocidade no topo da rampa.
Ver solução completaQuestão 23
Uma pequena esfera de massa está pendurada no teto por uma corda de comprimento como indicado na figura. Uma força constante é aplicada à esfera na direção horizontal deslocando-a lentamente desde a posição quando a corda está na vertical até quando a corda faz um ângulo com a vertical. O caminho que a esfera percorre é o arco de círculo . Sabendo que a esfera se encontra em repouso antes e depois do deslocamento, responda em função dos dados do problema. Utilize para a aceleração da gravidade.
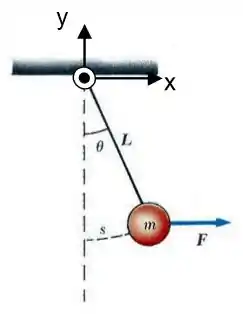
a) Escreva em notação vetorial (em termos dos vetores unitários e ) a tensão na corda para a posição indicada na figura.
b) Desenvolva o teorema trabalho-energia para a situação descrita.
c) Calcule os trabalhos realizados pela tensão, força da gravidade e força . Justifique cada um dos seus cálculos.
d) A origem do potencial está onde a corda está presa no teto. Calcule o valor da energia potencial gravitacional da esfera para posição indicada na figura.
Ver solução completaQuestão 24
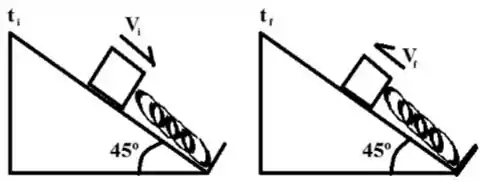
1a) Na figura, um bloco de tem velocidade inicial em um instante quando se choca com uma mola relaxada . O bloco comprime a mola até um valor máximo e depois a mola empurra de volta o bloco até o ponto inicial. Neste instante, , a velocidade final é . Durante todo percurso existe atrito cinético. Calcule o trabalho da gravidade , o trabalho da mola e o trabalho do atrito entre os instantes e .
Questão 27
Um bloco de massa m=3,0 Kg, partindo do repouso, é puxado sobre uma superfície horizontal sem atrito por uma força F cuja direção é sempre constante e horizontal. O módulo da força é variável, conforme o gráfico ao lado.
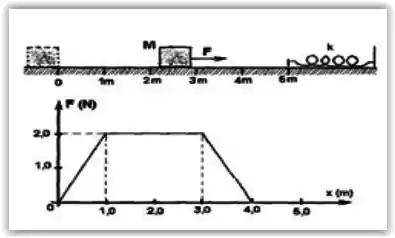
(a) Determine o trabalho realizado pela força desde x = 0 até 5,0 m.
(b) Calcule a velocidade do bloco quando ele atinge a posição x = 5,0 m.
(c) Após percorrer toda a superfície mostrada na figura o bloco é freado por uma mola de constante elástica k = 300 N/m. Determine a compressão máxima da mola.
Ver solução completaQuestão 28
Um pêndulo simples é formado por uma massa , presa a um fio ideal de comprimento , que tem uma de suas extremidades presa a um suporte no teto. O pêndulo é abandonado, em repouso, na posição horizontal. As forças que atuam no pêndulo são o peso, a tração e a resistência do ar. O pêndulo realiza seu movimento conforme a trajetória pontilhada até inverter o seu movimento, quando faz um ângulo com a vertical, conforme a figura.
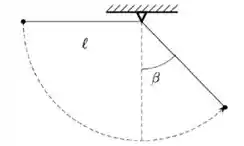
Qual o trabalho realizado pela força de resistência do ar no deslocamento entre os instantes em que o pêndulo é abandonad e aquele no qual ele faz o ângulo com a vertical, indicado na figura?
a)
b)
c)
d)
e)
f)
g)
Ver solução completaQuestão 29
Uma bala de massa atinge o solo com velocidade de módulo . Após penetrar no solo, ela percorre, em linha reta, uma distância até para num intervalo de tempo . Qual o módulo da força média total exercida sobre a bala durante este intervalo de tempo?
Escolha uma:
Questão 30
Um objeto de massa desliza na direção do eixo-x positivo em uma superfície com coeficiente de atrito cinético . O objeto tem uma velocidade quando colide de forma perfeitamente inelástica com uma mola quando ela está no seu ponto de equilíbrio (relaxada). A mola tem uma constante elástica . Durante a compressão da mola o atrito é desprezível. O objeto para momentaneamente, depois de comprimir a mola uma distância . O objeto é então forçado pela mola a se mover na direção do eixo-x negativo junto com a mola passando de novo pelo ponto de equilíbrio até parar momentaneamente a uma distância deste ponto. Considere o objeto como uma massa pontual. Utilize conservação de energia nas respostas abaixo. Justifique seus cálculos.
Dados:
a) Calcule o trabalho sobre o objeto desde o momento em que ele encosta na mola até parar momentaneamente.
b) Determine a distância d que a mola foi comprimida até parar momentaneamente.
c) Determine a velocidade quando o objeto passa pela posição de equilíbrio na volta, isto é se movendo na direção do eixo-x negativo.
d) Lembre que na volta a mola fica presa no objeto. Determine a distância D que a mola foi distendida até parar momentaneamente.
Ver solução completaQuestão 32
Uma pedra é lançada verticalmente, do solo, com velocidade de módulo v0. Verifica-se que ao retornar ao solo o módulo de sua velocidade é , onde . Durante o movimento da pedra, considere somente a ação das forças peso , e a força de resistência do ar . Para o trabalho da força de resistência do ar no
percurso ida e volta, a resposta correta é:
a) pois
b) pois
c) pois a posição final coincide com a posição final da pedra
d) pois
e) Nenhuma resposta anterior está correta.
Ver solução completaQuestão 33
Um bloco de 4 kg é empurrado a partir do repouso por uma mola comprimida, que não obedece a Lei de Hooke. A força dessa mola é dada por , onde x se mede a partir do comprimento de equilíbrio da mola. Ao passar pela posição de equilíbrio, o bloco desprende-se passando a movimentar-se em uma região com coeficiente de atrito dinâmico de 0,25, percorrendo uma distância de 10 m até parar. A velocidade máxima atingida pelo bloco e a compressão da mola são, respectivamente:
- e m
- e m
- e e m
- e m
- e m
Questão 34
Em um local cuja aceleração gravitacional tem módulo , um corpo de massa é liberado a partir do repouso do alto de um edifício.
Durante a queda, o corpo sofre a ação das forças gravitacional e de arrasto devido à resistência do ar.
Sabe-se que o corpo atingiu velocidade de módulo após percorrer uma altura . O trabalho realizado pela força de arrasto sobre o corpo nesse trecho é igual a:
Questão 35
Uma moeda de massa é abandonada a partir do repouso do topo do edifício Itália, em São Paulo, que tem aproximadamente metros de altura. A moeda atinge a velocidade limite de antes de atingir o chão.
O trabalho da força de arraste durante todo o trajeto de queda da moeda é de:
Ver solução completa
Questão 36
Uma partícula de massa realiza um movimento circular. Se a sua energia cinética variou ao longo desse movimento então podemos afirmar que:
isso era esperado já que a força resultante é não-nula.
a variação da energia cinética é igual ao trabalho realizado pela força centrípeta.
isso era esperado já que a velocidade muda de direção ao longo do movimento.
a força resultante deve ter uma componente tangencial.
nenhuma das outras alternativas.
Ver solução completaQuestão 37
Preencha cada campo com sua resposta.
Uma partícula percorre o eixo sujeita à ação de uma única força , com em metros e em newtons, conforme mostra a figura .
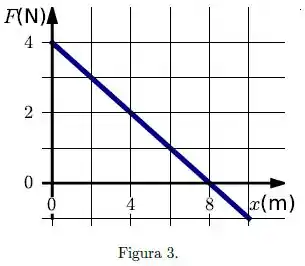
A partícula encontra-se em repouso em . Logo:
- A variação da energia cinética entre e é __.
- A partícula atinge sua velocidade máxima na posição .
Questão 38
A componente de um força (em newtons) em função da posição (em metros) que atua sobre um corpo enquanto este se desloca ao longo do eixo é representada na figura abaixo. Sabe-se que em o corpo se encontra em repouso. A energia cinética em é igual a:
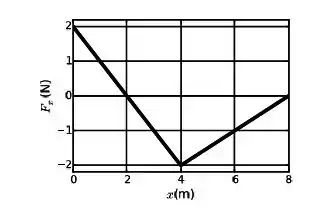
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 39
Um automóvel de massa é conduzido em um declive de a uma velocidade de quando acontece um defeito com suas rodas e elas travam. Ele passa então a deslizar sob a ação de uma força de atrito constante de que causa uma parada total do veículo.
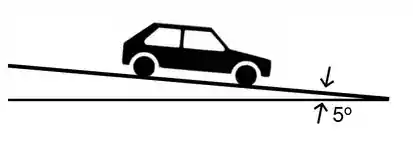
Dados: ; ; ;
Determine a aceleração do automóvel.
Determine o trabalho realizado pela força gravitacional.
Determine trabalho do atrito.
De acordo com seus resultados anteriores diga se foi possível confirmar, para a situação apresentada, a validade do teorema do trabalho e da energia cinética? Justifique.
Ver solução completaQuestão 40
Uma partícula se desloca no sentido positivo do eixo sujeita a uma única força , mostrada na figura. Sejam , e os módulos das velocidades em , e respectivamente.
Baseando-se apenas numa análise da figura abaixo, determine a alternativa correta:
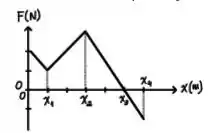
(a)
(b)
(c)
(d)
(e)
(f)
Ver solução completaQuestão 41
Na figura abaixo, um bloco de massa desliza ao longo de uma pista, de um nível para outro mais elevado, passando por um vale intermediário. A pista não possui atrito até o bloco atingir o nível mais alto, onde uma força de atrito faz o bloco parar ao percorrer uma distância . A velocidade do bloco no ponto é , a diferença de altura é e coeficiente de atrito cinético é . Considere .
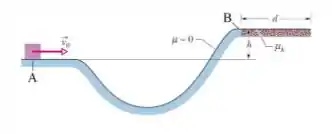
Determine:
(a) A variação da energia potencial gravitacional quando o bloco se desloca de para .
(b) O módulo da velocidade inicial .
(c) A distância .
Ver solução completaQuestão 42
Um fio ideal tem uma de suas extremidades presa no teto e passa por duas polias também ideais. Uma lata com uma massa está pendurada em uma das polias (por um fio também ideal) e uma força de módulo desconhecido é aplicada por uma pessoa na extremidade livre do fio de maneira que a lata sobe com velocidade constante. A situação está representada na figura ao lado.
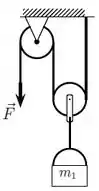
(b) Qual o trabalho realizado por cada uma das forças que atuam sobre a lata quando a
mesma sobe uma distância conhecida?
Ver solução completaQuestão 43
[Enunciado comum às Questões 3 e 4]
Um bloco de massa repousa em uma superfície horizontal sem atrito e está preso a uma mola de constante elástica e massa desprezível. A extremidade oposta da mola é mantida presa a uma parede. O bloco está em repouso na posição em que a mola está relaxada (). Nesta situação uma força constante ́é aplicada no sentido positivo do eixo . A figura mostra o gráfico da energia cinética do bloco em função da posição após a aplicação da força. Considere .
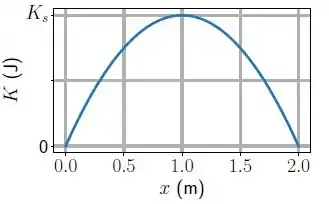
[Questão 4]
O módulo da força ́é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 44
Parte I
Uma caixa de massa é levantada verticalmente (eixo 𝑦) do solo a partir do repouso por um motor através de um cabo ideal fixado na caixa. A força de tração é dada pela função , onde ; ; . O motor funciona somente no intervalo , ao fim do qual é desligado, deixando de produzir a tração. Use as leis da dinâmica e de energia para calcular o que for pedido. Use .
(a ) Calcule o trabalho realizado pela tração do cabo desde o solo até o motor desligar.
(b ) Faça um diagrama de forças na subida. Obtenha o valor da velocidade da caixa no instante em que ela alcança de altura.
Parte II
Revistas automobilísticas em 2016 citam carros superesportivos elétricos capazes de partir do repouso e atingir a velocidade de propulsionados por dois motores elétricos e baterias elétricas, em menos de . Sites de internet especializados mencionam uma potência equivalente a para um veículo com . Estimativas de perdas de energia devido a processos internos entregam uma potência útil equivalente a da potência original para o movimento do automóvel.
Encontre a força instantânea gerada pela potência útil ao atingir essa velocidade.
Ver solução completaQuestão 45
Um bloco de metal de massa está apoiado numa mesa e está conectado a um bloco de massa através uma corda de massa desprezível. A corda passa por uma polia de massa desprezível, na qual não há atrito. Ao iniciar o movimento, vemos que há atrito cinético sobre a mesa, com coeficiente .
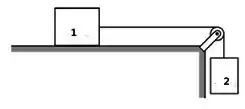
Depois que os blocos se deslocaram de uma distância , podemos dizer que :
- o bloco 1 ganhou energia cinética .
- energia cinética do sistema é que é igual a .
- a energia cinética do bloco 2 é K =
- a energia cinética do sistema é que é igual a
- nenhuma das anteriores.
Questão 46
Um bloco de massa é lançado em um plano inclinado, fazendo um ângulo com o solo, com velocidade inicial . Ele sobe, atinge o ponto mais alto da trajetória, e retorna à posição inicial. Considerando a aceleração gravitacional e o coeficiente de atrito cinético , responda às seguintes questões:
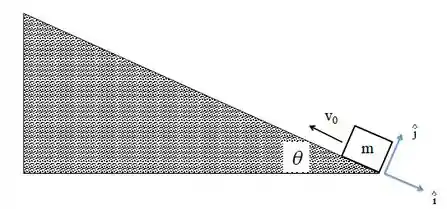
(a) Faça o diagrama de forças que atuam sobre o corpo no início do movimento.
(b) Descreva os valores das forças indicadas no item anterior em termo das variáveis do enunciado.
(c) Qual a distância total percorrida pelo corpo na subida?
(d) Qual o trabalho realizado pela força peso e pela força de atrito ao longo da subida.
(e) Qual o trabalho realizado pela força peso e pela força de atrito ao longo da descida.
(f) Qual a variação da energia cinética no trajeto total do corpo?
Ver solução completaQuestão 48
Uma bola de massa é lançada do solo com uma velocidade inicial de módulo em uma direção que faz um ângulo com a horizontal. Durante todo seu movimento ela está sob a ação da força peso e da força de resistência do ar. Observa-se que a bola atinge o ponto de altura máxima , com velocidade de módulo . Qual o trabalho realizado pela força de resistência do ar entre o lançamento da bola e o instante em que ela atinge a altura máxima?
Ver solução completaQuestão 49
Um bloco de massa desliza para a direita de encontro a uma mola de constante elástica . Quando atinge a mola, a velocidade do bloco é igual a . O bloco para momentaneamente após comprimir a mola de . Qual é o módulo da força de atrito exercida pelo piso sobre o bloco?
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 50
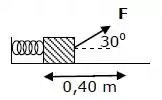
Um bloco de está em repouso sobre uma superfície horizontal e preso a uma mola de constante elástica . O bloco é arrastado, distendendo a mola de , pela força como mostra a figura. A força de atrito da superfície sobre o bloco é de . Dado que , e , a velocidade do bloco no final deste deslocamento é
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 51
No instante , uma partícula de massa tem uma velocidade de . Em , sua velocidade é . Neste intervalo de tempo, o trabalho feito sobre a partícula foi:
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 52
Um corpo desliza em um piso horizontal no sentido positivo do eixo enquanto uma força age sobre ele. O corpo parte do repouso na posição e se move até ficar momentaneamente em repouso.
(a) Expresse o trabalho realizado pela força sobre o corpo em função da posição final . Considere como posição inicial .
(b) Esboce o gráfico da forças versus posição. Determine o valor máximo da energia cinética adquirida pelo corpo e em que posição ela ocorre.
(c) Determine, depois de iniciado o movimento, em que posição o corpo fica em repouso momentaneamente?
Ver solução completaQuestão 53
[Enunciado comum às Questões 3 e 4]
Um bloco de massa repousa em uma superfície horizontal sem atrito e está preso a uma mola de constante elástica e massa desprezível. A extremidade oposta da mola é mantida presa a uma parede. O bloco está em repouso na posição em que a mola está relaxada (). Nesta situação uma força constante ́é aplicada no sentido positivo do eixo . A figura mostra o gráfico da energia cinética do bloco em função da posição após a aplicação da força. Considere .
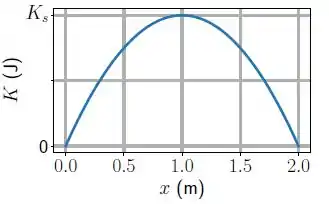
[Questão 3]
Julgue as assertivas abaixo, considerando que o bloco move-se na direção do eixo positivo:
. A variação de energia cinética é igual ao trabalho da força .
. O trabalho da força elástica é negativo.
. A energia mecânica total do sistema é .
É correto apenas o que se afirma em:
(a)
(b)
(c)
(d) e
(e) e
(f) e
(g) Todas
(h) Nenhuma
Ver solução completaQuestão 54
Uma partícula de massa se move sob a ação de uma força constante, partindo de um ponto inicial até um ponto final . É correto afirmar que
(A) O trabalho realizado pela força depende do caminho percorrido entre os pontos e , mas a variação de energia cinética não.
(B) O trabalho realizado pela força e a variação de energia cinética dependem do caminho percorrido entre os pontos e
(C) O trabalho realizado pela força não depende do caminho percorrido entre os pontos e , assim como a variação de energia cinética
(D) O trabalho realizado pela força não depende do caminho percorrido entre os pontos e , mas a variação de energia cinética sim
(E) O trabalho realizado pela força é necessariamente nulo, assim como a variação da energia cinética
Ver solução completaQuestão 55
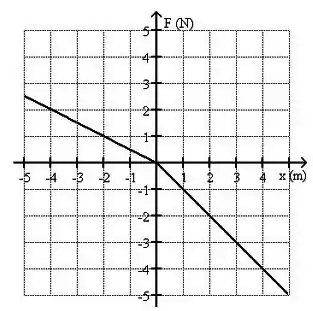
Uma partícula de massa move-se ao longo do eixo sujeita a uma força que varia com a posição conforme o gráfico ao lado. Se a velocidade da partícula é quando ela passa por , qual é a sua velocidade quando ela passa por ?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 56
Uma partícula parte do repouso em e se move até sob a ação de uma força variável , que é mostrada na figura abaixo. Quais as energias cinéticas da partícula em e em ?
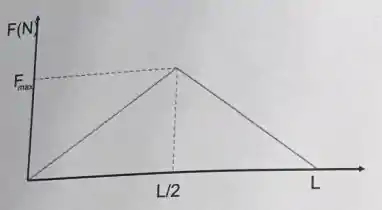
a) ,
b) ,
c) ,
d) ,
e) ,
Ver solução completaQuestão 57
Duas bolas e , de massas e diferentes, colidem elasticamente. Inicialmente a bola tem velocidade , onde é uma constante positiva, e a bola está em repouso. Após a colisão a bola passa a se mover com velocidade , na direção perpendicular à direção do movimento inicial. Considere o plano da colisão como sendo horizontal e despreze as forças de atrito.
(e) Suponha agora uma outra situação, onde estas bolas se chocam de forma inelástica, sendo que a energia cinética final do sistema equivale à metade da energia cinética inicial. Qual será o trabalho realizado pelas forças dissipativas presentes neste sistema?
Ver solução completaQuestão 59
Uma caixa de em repouso sobre uma superfície horizontal é erguida verticalmente até uma altura de , mediante a aplicação de uma força vertical de . Encontre a energia cinética final da caixa.
Ver solução completaQuestão 60
Um corpo de dimensões desprezíveis e de massa é liberado a partir do repouso da borda de um poço semiesférico de raio . Ele desliza pela parede do poço e, após algumas oscilações em torno do fundo do poço, permanece em repouso nesta posição. Para as forças presentes desde o início até o fim do movimento do corpo é correta a opção:
a) o trabalho da força peso é ;
b) o trabalho da força normal que a superfície do poço exerce sobre o corpo não é nulo;
c) o trabalho total das forças dissipativas é nulo;
d) o trabalho total das forças dissipativas é ;
e) o trabalho total das forças dissipativas é .
Ver solução completaQuestão 63
Uma força paralela ao eixo é aplicada a um trenó de massa que se desloca sobre uma superfície lisa (sem atrito). A força tem direção e sentido de e seu componente varia com a coordenada do modo indicado no gráfico.
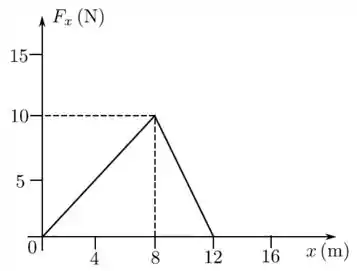
A opção CORRETA é
- A variação de energia cinética é nula entre e
- O trabalho da força é positivo entre e e negativo entre e
- A variação de energia cinética é igual a , entre m e
- A variação de energia potencial é igual a , entre e
- A variação de energia mecânica é igual a , entre x = 0 m e x = 12 m
Questão 64
Um objeto de massa possui, em um certo instante escolhido como , uma energia cinética de e se move em uma dimensão, escolhida como o eixo OX. O gráfico abaixo representa a força resultante a que está submetido o objeto.
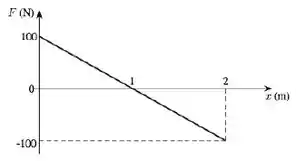
Sobre a energia cinética do objeto quando chega à posição é correto afirmar que:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Ver solução completaQuestão 65
Uma moeda de massa é abandonada a partir do repouso do topo do edifício Itália, em São Paulo, que tem aproximadamente metros de altura. A moeda atinge a velocidade limite de antes de atingir o chão.
Após atingir a velocidade limite, o módulo da potência dissipada pela força de arraste do ar é:
Ver solução completa
Questão 66
1. Um caminhão de três toneladas está sendo embarcado num navio por um guindaste que exerce uma força de , para cima, sobre o veículo. Esta força, suficiente para provocar o início da subida do caminhão, atua sobre uma distância de dois metros. Calcule
(c) a velocidade de subida do caminhão depois dos dois metros.
Ver solução completaQuestão 67
No instante , uma partícula de tem uma velocidade de . No instante , a velocidade da partícula é . Durante esse intervalo de tempo, o trabalho executado sobre a partícula é:
Ver solução completa
Questão 68
Um bloco está em repouso sobre um plano inclinado muito longo. A inclinação do plano é de com a horizontal. Repentinamente uma força impulsiva atua sobre o bloco em direção à base do plano, produzindo uma velocidade inicial de . O bloco para após percorrer . Qual é o valor do coeficiente de atrito cinético entre o bloco e o plano?

Questão 69
. A força resultante age sobre uma partícula de massa , que move-se ao longo do eixo , de tal forma que a sua posição em função do tempo é dada por:
com em metros e em segundos. O trabalho realizado pela força sobre a partícula de até , em Joules, é:
Ver solução completaQuestão 70
. Uma partícula move-se ao longo do eixo sob a ação de uma única força , conservativa, que dá origem à energia potencial
onde é medido em metros e é medido em joules. O trabalho, em Joules, realizado pela força quando a partícula se movimenta de até é:
Ver solução completaQuestão 72
Suponha que uma pessoa, cuja massa , se desloque em uma superfície plana e sem atrito com velocidade igual a . A medida que ela vai se deslocando ela vai recolhendo caixas de massa cada. Qual deve ser o trabalho realizado pela pessoa ao final da coleta das caixas?
(OBS: note que a velocidade da pessoa ao final do trajeto é aproximadamente igual a )
(a)
(b)
(c) ;
(d) ;
(e) ;
Ver solução completaQuestão 73
Dois trenós apostam uma corrida sobre um lago congelado sem atrito. Os trenós possuem massas e , respectivamente. A vela de um trenó é idêntica à do outro, de modo que o vento exerce a mesma força constante sobre cada trenó. Os dois trenós partem do repouso e a distância entre a partida e a linha de chegada é igual a . Qual a razão entre a energia cinética do trenó e a energia cinética do trenó , na reta de chegada?
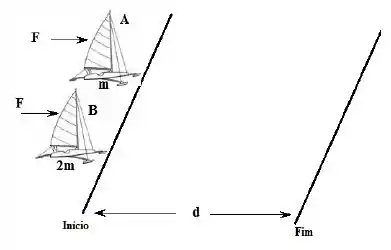
Ver solução completa
Questão 74
Uma força constante de módulo age sobre um bloco de massa , que pode se mover sobre uma superfície sem atrito. Assinale a alternativa incorreta.
se o bloco realiza um percurso fechado, o trabalho da força é nulo.
o trabalho realizado pela força pode ser negativo, dependendo do ângulo entre os sentidos de e o do movimento.
A força é conservativa se a direção do movimento for a mesma da direção de aplicação da força.
É possível definir uma energia potencial relacionada à força .
O trabalho da força é igual à variação da energia cinética do bloco somente se esta for a força resultante aplicada ao bloco.
Ver solução completaQuestão 76
Um próton com massa igual a é impulsionado com uma velocidade inicial de diretamente contra um núcleo de urânio situado a uma distância de . O próton é repelido pelo núcleo de urânio com uma força de módulo , onde é a distância entre as duas partículas e . Suponha que o núcleo de urânio permaneça em repouso.
c) Qual é a velocidade do próton quando ele está novamente a uma distância de do núcleo de urânio?
Ver solução completaQuestão 79
Uma partícula de massa desloca-se ao longo de uma reta. Entre e , ela está sujeita à uma força representada no gráfico da figura . Calcule a velocidade da partícula depois de percorrer e , sabendo que sua velocidade para é de .
Ver solução completaQuestão 80
Um pequeno bloco com massa de está ligado a um fio que passa através de um buraco em uma superfície horizontal sem atrito (figura abaixo). Inicialmente, o bloco gira a uma distância de do buraco com uma velocidade de . A seguir, o fio é puxado para baixo, fazendo o raio do círculo encurtar para . Nesta nova distância verifica-se que sua velocidade passa para .
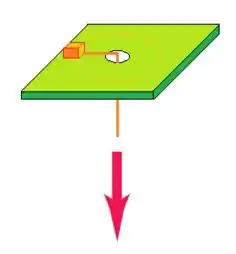
c) Qual foi o trabalho realizado pela pessoa que puxou o fio?
Ver solução completaQuestão 81
Uma partícula de 4,0 kg, com velocidade inicial igual a 2m/s na posição x = 0m, acelera ao longo do eixo x sujeita a uma força variável representada pelo gráfico mostrado na figura. Sobre a velocidade instantânea da partícula, é CORRETO afirmar que:
Marque a afirmação CORRETA a respeito do trabalho total realizado após as repetições
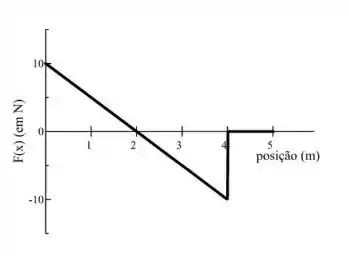
a) é -2m/s na posição x = 4m
b) é nula na posição x = 2m
c) é nula na posição x = 5m
d) é 3m/s na posição x = 2m
e) é √5 m/s na posição x = 2m
Ver solução completaQuestão 82
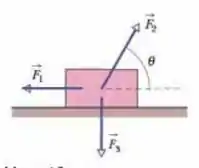
(Capítulo 7.5 – Exercício 13) A Fig. 7-27 mostra três forças aplicadas a um baú que se desloca para a esquerda sobre um piso sem atrito. Os módulos das forças são , e ; o ângulo indicado é . No deslocamento, (a) qual é o trabalho total realizado sobre o baú pelas três forças e (b) a energia cinética do baú aumenta ou diminui?
Questão 83
(Capítulo 7.5 – Exercício 15) Uma força de e orientação fixa realiza trabalho sobre uma partícula que sofre um deslocamento . Qual é o ângulo entre a força e o deslocamento se a variação da energia cinética da partícula é
(a) e (b)?
Ver solução completaQuestão 84
(Cap 7 – Ex 10) Um bloco de gelo flutuante é colhido por uma correnteza que aplica ao bloco uma força , fazendo com que o bloco sofra um deslocamento . Qual é o trabalho realizado pela força sobre o bloco durante o deslocamento?
Ver solução completaQuestão 85
(Capítulo 7.7 – Exercício 27) Uma mola e um bloco são montados como na Fig. 7-9. Quando o bloco é puxado para o ponto , devemos aplicar uma força de para mantê-lo nessa posição. Puxamos o bloco para o ponto e o liberamos. Qual é o trabalho realizado pela mola sobre o bloco quando este se desloca de para (a) , (b) , (c) e (d) ?
Ver solução completaQuestão 86
(Capítulo 7.7 – Exercício 29) A única força que age sobre um corpo de enquanto se move no semieixo positivo de um eixo x tem uma componente, com x em metros. A velocidade do corpo em é 8. (a) Qual é a velocidade do corpo em ? (b) Para que valor positivo de x o corpo tem uma velocidade de ?
Ver solução completaQuestão 87
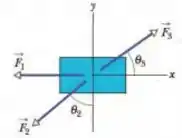
(Capítulo 7.5 – Exercício 16) A Fig. 7-26 mostra uma vista superior de três forças horizontais atuando sobre uma caixa que estava inicialmente em repouso e passou a se mover sobre um piso sem atrito. Os módulos das forças são , , e e os ângulos indicados são e . Qual é o trabalho total realizado sobre a caixa pelas três forças nos primeiros de deslocamento?
Questão 88
(Capítulo 7.5 – Exercício 12) Um objeto de está se movendo no sentido positivo de um eixo . Quando passa pelo ponto , uma força constante dirigida ao longo do eixo passa a atuar sobre ele. A Fig. 7-28 mostra a energia cinética em função da posição quando o objeto se desloca de a ; . A força continua a agir. Qual é a velocidade do objeto no instante em que passa pelo ponto ?
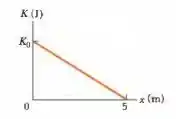
Questão 89
(Cap 7 – Ex 7) A única força que age sobre uma lata de que está se movendo em um plano tem um módulo de . Inicialmente, a lata tem uma velocidade de no sentido positivo do eixo ; em um instante posterior, a velocidade passa a ser no sentido positivo do eixo . Qual é o trabalho realizado sobre a lata pela força de nesse intervalo de tempo?
Ver solução completaQuestão 90
. Um corpo desliza em um piso horizontal no sentido positivo do eixo enquanto uma força age sobre ele. O corpo parte do repouso na posição e se move até ficar momentaneamente em repouso. Determine o valor máximo da energia cinética adquirida pelo corpo e em que posição ela ocorre, determine também, depois de iniciado o movimento em que posição o corpo fica em repouso momentaneamente.
Ver solução completaQuestão 91
Um anel de massa , ligado a duas molas de constantes elásticas iguais a e , pode deslizar sem atrito sobre um trilho rígido horizontal, como mostra a figura, na qual está indicado um sistema de eixos , com na direção do trilho. Inicialmente o anel se encontrava em repouso sobre o trilho na posição onde as duas molas estão relaxadas. A partir do instante o anel passou a sofrer a ação de uma força constante , numa direção que faz um ângulo com a horizontal, levando o anel a oscilar em torno de um novo ponto de equilíbrio.
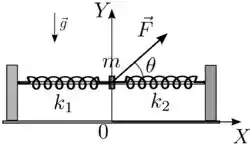
- Qual a força total que o trilho exerce sobre o anel?
- Em que posição é nula a resultante das forças que atuam sobre o anel?
- Escreva a energia potencial elástica do sistema em função da coordenada do anel.
- Escreva a energia potencial associada à força constante em função da coordenada do anel.
- Expresse o módulo da velocidade do anel em função de sua coordenada .
Questão 92
Uma partícula parte do repouso em e desloca-se para , sob a ação de uma força variável mostrada na figura. Qual é a energia cinética das partículas em e em ?
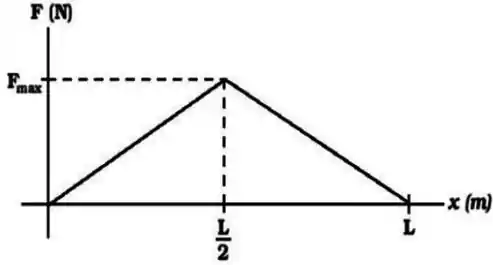
a)
b) ,
c) ,
d) ,
e) ,
Ver solução completaQuestão 93
O cabo de um elevador de rompe-se, quando ele está parado no primeiro andar. No instante do rompimento, o piso do elevador encontra-se a uma distância acima de uma mola amortecedora, cuja constante de mola é . Um sistema de segurança prende os trilhos laterais que servem de guia, de modo que uma força de atrito constante de opõe-se ao movimento do elevador após o rompimento do cabo. Determine:
b) A deformação máxima da mola;
Ver solução completaQuestão 94
O cabo de um elevador de rompe-se, quando ele está parado no primeiro andar. No instante do rompimento, o piso do elevador encontra-se a uma distância acima de uma mola amortecedora, cuja constante de mola é . Um sistema de segurança prende os trilhos laterais que servem de guia, de modo que uma força de atrito constante de opõe-se ao movimento do elevador após o rompimento do cabo. Determine:
A altura que o elevador subirá de volta, a partir da posição inicial da mola relaxada;
Ver solução completaQuestão 95
Um bloco de massa é solto do repouso de uma altura desconhecida acima de uma mola relaxada posicionada na vertical e com constante elástica. O bloco gruda na mola e a comprime de até parar momentaneamente. Despreze atritos.
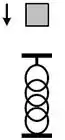
a) Calcule o trabalho realizado pela força da gravidade sobre o bloco durante a compressão da mola.
b) Calcule o trabalho realizado pela mola sobre o bloco durante a sua compressão.
c) Calcule o módulo da velocidade do bloco imediatamente antes dele colidir com a mola.
Ver solução completaQuestão 96
Uma mola tem uma extremidade fixa em uma parede vertical e a outra num carrinho de massa , que se movimenta como uma partícula numa superfície horizontal sem atrito sujeita a uma força elástica dada por . Se o carrinho passa pela posição com velocidade , sua velocidade escalar ao passar pela posição , em metros por segundo, é:
Questão 97
A força resultante age sobre uma partícula de massa , que move-se ao longo do eixo , de tal forma que a sua posição em função do tempo é dada por:
com em metros e em segundos. O trabalho realizado pela força sobre a partícula de
s até s, em Joules, é?
Ver solução completaQuestão 98
Um corpo de está sob a ação de uma força que gera um deslocamento dado por (em metros). O trabalho feito pela força em segundos é:
A.
B.
C.
D.
E.
Ver solução completaQuestão 99
A quantidade de trabalho necessária para, a partir do repouso, colocar um objeto se movendo é igual a:
a) velocidade final do objeto
b) energia cinética final do objeto
c) velocidade quadrada final do objeto
d) massa do objeto vezes sua aceleração
e) massa do objeto vezes sua velocidade final
Ver solução completaQuestão 100
Um bloco de gelo com massa de está inicialmente em repouso sobre uma superfície horizontal sem atrito. A seguir, um trabalhador aplica uma força horizontal sobre ele. Como resultado, o bloco se move ao longo do eixo de tal modo que sua posição em função do tempo é dada por , onde e .
c) Calcule o trabalho realizado pela força durante os primeiros do movimento.
Ver solução completaQuestão 101
Um bloco de massa repousa sobre uma superfície horizontal sem atrito e está preso a uma mola também na horizontal de constante elástica cuja outra extremidade é mantida fixa. A mola está relaxada e o bloco está em repouso na posição inicial quando uma força horizontal é aplicada no sentido do eixo positivo. O gráfico abaixo mostra como a energia cinética do bloco varia em função da posição durante a aplicação das forças.
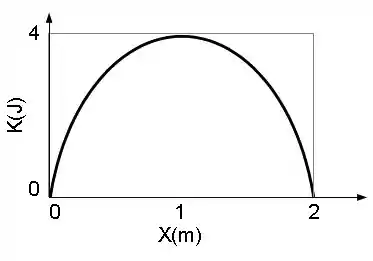
(a) Escreva o teorema Trabalho-Energia Cinética para as forças que atuam no bloco.
(b) Calcule o trabalho realizado pela mola de até
(c) Calcule o trabalho realizado pela força de até .
Ver solução completaQuestão 102

Um bloco de massa é solto do repouso de uma altura (posição A) na pista ilustrada na figura abaixo. A pista é sem atrito, a menos do trecho BC de comprimento . O bloco chega à mola de constante elástica desconhecida e a comprime de uma distância até chegar a um repouso momentâneo. As respostas devem ser dadas em função das variáveis do problema ( e ) e da aceleração da gravidade . Explicite em todos os itens os teoremas utilizados.
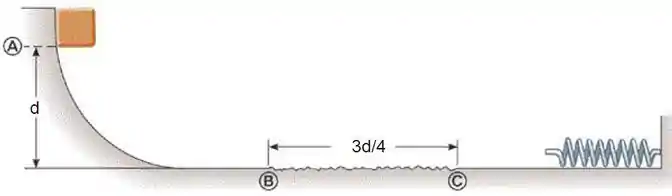
a) Determine a energia cinética com que o bloco chega à posição B e o trabalho realizado pela força da gravidade da posição A até a posição B.
b) Sabendo que o bloco chega à posição C com metade da velocidade com que ele chegou em B calcule trabalho realizado pelo atrito e o coeficiente de atrito cinético do trecho BC.
c) Determine o trabalho realizado pela mola desde quando ela estiver relaxada até quando estiver totalmente comprimida. Determine a constante elástica da mola.
d) O bloco agora retorna empurrado pela mola. Determine a altura máxima que ele alcança.
Ver solução completaQuestão 103
Um bloco A de massa está conectado a um bloco B de massa e a uma mola ideal de constante elástica . A corda e a roldana são também ideais. O bloco A está sobre uma superfície horizontal e o bloco B está sobre um plano inclinado que faz com a horizontal um ângulo, e ambas as superfícies oferecem aos blocos atrito de mesmo coeficiente cinético. Inicialmente os blocos estão em repouso e a mola está relaxada. Devido às forças em jogo, o sistema sai do repouso e vai se deslocar uma distância até parar momentaneamente. Determine, em termos dos parâmetros pertinentes:
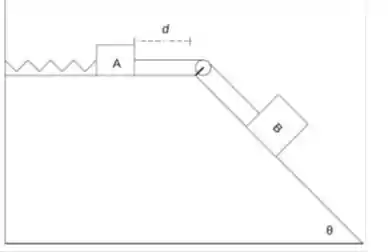
(a) o trabalho da força elástica realizado pela mola sobre o sistema dos blocos nesse deslocamento;
(b) o trabalho realizado pela força gravitacional sobre o sistema;
(c) os trabalhos e realizados pelas forças de atrito e pelas forças normais sobre o sistema.
Considere agora os seguintes valores: , , e
(d) Determine o valor de .
Ver solução completaQuestão 104
Na figura abaixo é apresentado o comportamento de uma força aplicada em um bloco em função da sua posição. Se o bloco se encontra em repouso instantâneo no ponto , é possível afirmar que:
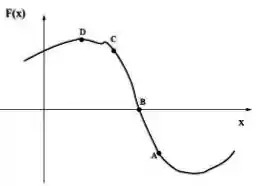
Ele volta a estar em repouso nas proximidades do ponto .
Ele volta a estar em repouso nas proximidades do ponto .
Ele terá sua maior energia cinética no ponto .
Ele se deslocará na direção de positivo.
A energia potencial apresenta um máximo no ponto .
Ver solução completaQuestão 105
Qual das seguintes afirmações a respeito do trabalho realizado por uma força conservativa agindo sobre uma partícula é INCORRETA
(A) Depende das posições inicial e final da partícula, mas não depende de sua trajetória.
(B) Pode sempre ser expresso como a diferença entre os valores inicial e final de uma energia potencial.
(C) É nulo sempre que o ponto final da trajetória coincidir com o ponto inicial.
(D) Pode modificar a energia cinética da partícula.
(E) Não muda de valor quando o sentido de percurso da trajetória da partícula é invertido:
Ver solução completaQuestão 106
Um grande bloco de massa se movimenta horizontalmente através de uma distância total de sobre um piso com atrito a partir do repouso. Um trator empurra o bloco durante os primeiros com uma força variável, descrita pelo gráfico abaixo:
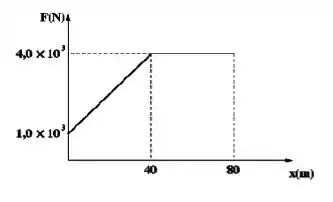
Dado: (capa da prova)
(a) Calcule o trabalho total realizado pelo trator sobre o bloco.
(b) Ao final dos 100 𝑚, o bloco chega ao repouso. Encontre o coeficiente de atrito cinético entre o bloco e o piso.
(c) Ache a velocidade do bloco na posição 𝑥=80 𝑚.
Ver solução completaQuestão 107
Um bloco de massa inicialmente em repouso e a uma altura desliza para baixo sobre a superfície de um plano inclinado que faz um ângulo com a horizontal. O plano inclinado permanece em repouso enquanto o bloco desliza sobre ele. Depois de ter chegado à base do plano o bloco continua a deslizar por uma distância ao longo de uma superfície horizontal até entrar em repouso. O coeficiente de atrito cinético é o mesmo entre o bloco e ambas as superfícies. Utilize obrigatoriamente a Lei de Conservação de Energia.
Dados:
a) Determine o valor da energia potencial que o bloco possui assim que ele chega à superfície horizontal.
b) Determine o valor da energia cinética que o bloco possui assim que ele chega à superfície horizontal.
c) Determine a distância percorrida pelo bloco ao longo da superfície horizontal até ele entrar em repouso.
Ver solução completaQuestão 108
Um satélite artificial da Terra é transferido de uma órbita circular de raio R para outra de raio 2R. Durante a transferência é correto afirmar que:
- A energia potencial gravitacional aumentou pois a força gravitacional entre a Terra e o satélite realizou um trabalho negativo.
- A energia potencial gravitacional continua a mesma pois a força gravitacional entre a Terra e o satélite não realiza trabalho.
- A energia potencial gravitacional diminuiu pois a força gravitacional entre a Terra e o satélite realizou um trabalho negativo.
- A energia potencial gravitacional diminuiu pois a força gravitacional entre a Terra e o satélite realizou um trabalho positivo.
- A energia potencial gravitacional aumentou e a força gravitacional entre a Terra e o satélite não realiza trabalho.
- A energia potencial gravitacional diminuiu e a força gravitacional entre a Terra e o satélite não realiza trabalho.