Aplicações da Hidrodinâmica
Produzido por Leonardo de BemTeoria
Fala aí! A dinâmica é a parte da física que estuda o movimento dos corpos, é com ela que a gente aprende a dividir o espaço pelo tempo para encontrar a velocidade, por exemplo. Agora, quando a gente taca um “hidro” aí na frente, estamos particularmente interessados no movimento e no cálculo da velocidade dos fluidos, que tendem a se comportar de um jeito um pouquinho diferente.
Essa página aqui vai tratar mais das aplicações da hidrodinâmica (como o Tubo de Venturi) do que dos conceitos iniciais mesmo. Mas fica tranquilo, se é isso que você tá procurando, tenho tudo separadinho aqui pra você 😉👇
Tubo de Venturi
O tubo de Venturi é um equipamento desenvolvido para medir a velocidade de um fluido incompressível que passa por um tubo de diâmetro variável. Olha só, imagine que tenhamos um fluido que escoa dentro de um tubo desse tipo:
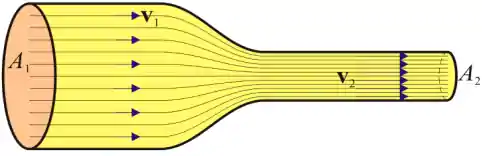
Aquela área da seção transversal
Tá, e onde que entra o tal do Venturi nessa história? Então, se a gente tiver um exemplo parecido com esse aí de cima, com uma velocidade de escoamento
Se liga, geralmente o tubo de Venturi vem com duas colunas instaladas, uma antes e uma depois da redução.
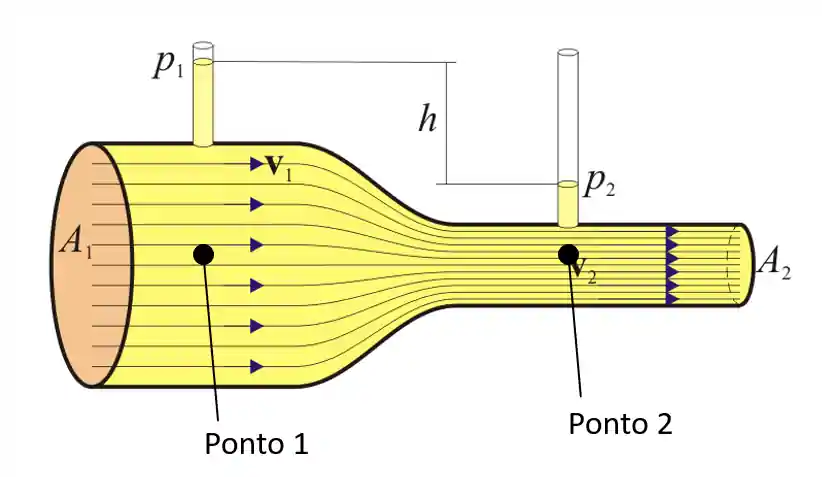
Vamos considerar dois pontos na mesma altitude, um embaixo da primeira coluna e outro embaixo da segunda. Podemos aplicar a equação de Bernoulli para esses dois pontos, da seguinte forma:
Como as alturas
Ou melhor:
Beleza, por enquanto usamos só Bernoulli. Agora, vamos usar o princípio de Stevin, lá da hidrostática, para calcular
A variação de altura entre as colunas é
Logo:
Agora, podemos substituir isso na equação anterior.
Repare que ficou
Mais uma sacada: se o fluido que viemos trabalhando é sempre o mesmo, aquela densidade
E, finalmente, chegamos no que queríamos. A velocidade de escoamento na seção menor vai ser:
Tudo isso parece teórico demais para um texto sobre aplicações, né? Mas pode acreditar, esse tubo de Venturi é muito utilizado em várias áreas do mundo real também. A aspiração de ar em um carburador, por exemplo, é realizada por meio de um tubo de Venturi.
Bernoulli e Lançamentos
Sabe aquele exemplo clássico que os livros adoram, de um tanque cheio de água com um vazamento por meio de um buraco ou um tubo? Vamos dar uma conferida:
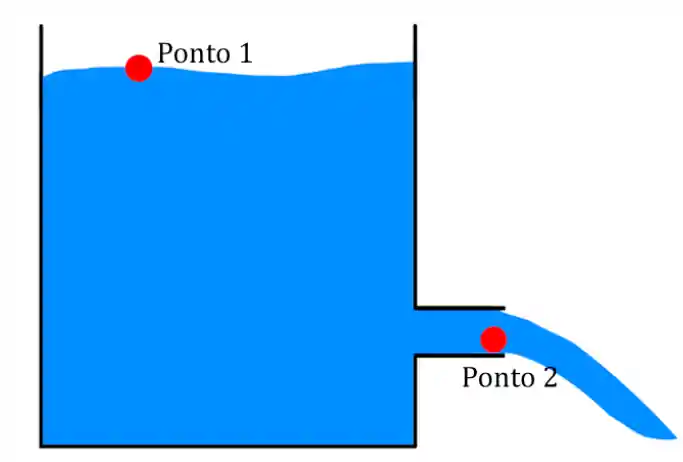
O que você faria se precisasse calcular a velocidade com que a água escoa por aquele tubo ali na lateral? Não sabe nem por onde começar? Então segue aqui comigo.
Identificamos dois pontos: o Ponto 1, na superfície do líquido do tanque, e o Ponto 2, na iminência da saída do tubo. O primeiro tem as seguintes características:
A pressão vai ser igual à atmosférica porque esse ponto tá lá na superfície, beleza? E a velocidade podemos aproximar para zero se considerarmos a superfície bem paradinha em relação à água que escoa ali pela lateral.
O segundo ponto vai ter a seguinte descrição:
Por que a pressão nesse ponto também é
Com isso, podemos escrever a equação de Bernoulli para esta situação.
E o resultado disso é:
Com isso em mãos, o problema passa a ser de lançamento oblíquo 😄.
A partir daí, vai depender do que o enunciado esteja te pedindo: pode ser o alcance máximo, a velocidade ao atingir o solo, a altura máxima… Mas essa velocidade que encontramos é a velocidade inicial do lançamento, beleza?
Sifão
Bora ver mais uma aplicação. Você pode já ter se deparado com uma questão que envolve uma figura parecida com essa aqui:
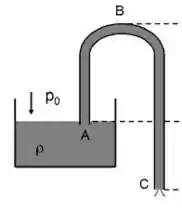
Esse tubo em “U” invertido é o que chamamos de sifão. Basicamente, ele é um instrumento usado para retirar o fluido de um lugar e escoá-lo para outro.
Geralmente, irão aparecer três pontos em questões desse tipo:
- O ponto onde ocorre a entrada do fluido (na nossa figura, o ponto
). - O ponto mais alto do sistema (ponto
). - O ponto onde ocorre a saída do fluido (ponto
).
Para calcular a velocidade de saída do líquido
Vamos começar aplicando Bernoulli entre os pontos
Essa é a velocidade de saída do líquido pelo ponto
E para acharmos a pressão no ponto mais alto?
Aplicamos Bernoulli novamente, dessa vez entre os pontos
Pelo princípio da continuidade, temos que
E para encontrar a altura máxima do ponto mais alto?
Vamos pegar essa última equação e isolar
Essa altura será máxima quando a pressão em
Tranquilo? Então bora fazer mais uns exercícios 😄
Bernoulli e Lançamentos
Sifão
Exercícios Resolvidos
Exercício Resolvido #1
Hugh D. Young e Roger A. Freedman, Física II – Termodinâmica e Ondas, 12a ed. São Paulo: Addison Wesley, 2008, pp 101 – Modificado
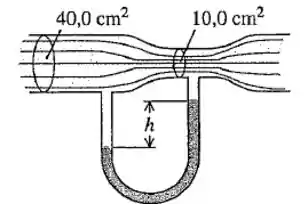
O tubo horizontal mostrado na figura apresenta seção reta com área igual a em sua parte mais larga e em sua constrição. A água flui no tubo, e vazão volumétrica é igual a (, Calcule:
- A velocidade do escoamento na parte mais larga e na constrição.
- A diferença de pressão entre essas duas partes.
- A diferença de altura entre os dois níveis de mercúrio existente no tubo em U.
Dado:
Passo 1
a)
Bom, como temos o valor da vazão, fica fácil calcular a velocidade em cada uma das áreas. Isso por causa do princípio da continuidade. Esse princípio nos diz que a vazão é constante. Então basta a gente usar a fórmula:
Na parte larga:
Se liga: Ali
E na constrição:
Viu como a velocidade aumenta quando a área transversal diminui? Isso acontece porque a vazão é constante (princípio da continuidade) =D
Passo 2
b)
Como o escoamento é horizontal podemos afirmar que: . Então, aplicando Bernoulli nos dois pontos (parte larga e constrição), vamos ter:
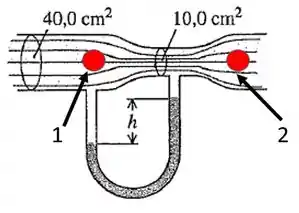
Galera, o problema pediu a diferença de pressão, por isso vamos isolar o termo como um todo.
Passo 3
c)
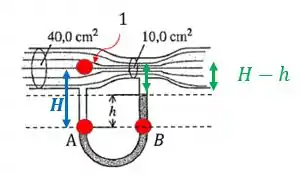
Pra calcular essa diferença vamos usar o os pontos A e B dessa figura acima! Nós vamos fazer porque o líquido no tubo em está parado e, portanto, podemos utilizar o princípio de Stevin:
A pressão no ponto A vai ser a pressão do ponto somada com a pressão feita pela coluna de água de altura
Já a pressão no ponto B vai ser a pressão no ponto B somada com as pressões das coluna de água (com altura ) e da coluna de mercúrio (com altura )
Passo 4
Igualando as pressões A e B
Expandindo esse termo com a densidade da água na direita podemos ver que vai cortar o termo
Agora basta isolar
Já calculamos no passo 2! Então agora é só substituir os valores e correr pro abraço!
Resposta
a)
b)
c)
Exercício Resolvido #2
Aula teórica, Fenômenos de Transporte, Profª. Érica Cristine
Água escoa em regime permanente no Venturi da figura. No trecho considerado, supõem-se as perdas por atrito desprezíveis e as propriedades uniformes nas seções. A área (1) é , enquanto a da garganta (2) é . Um manômetro, cujo fluido manométrico é mercúrio, é ligado entre as seções (1) e (2) e indica o desnível mostrado na figura. Pede-se a vazão da água que escoa pelo Venturi.
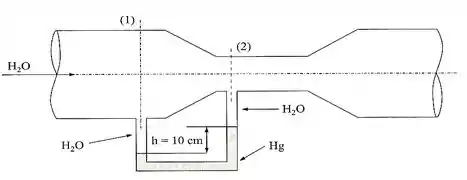
Considere
Passo 1
Queremos encontrar a vazão:
Para isso, precisamos da área e velocidade na seção (1) ou na seção (2).
Perceba que temos e .
Pela equação da continuidade, podemos relacionar e :
Passo 2
Substituindo valores:
Observe que não podemos determinar os valores de e , mas podemos relacioná-los.
Então, vamos aplicar a equação de Bernoulli entre os pontos (1) e (2).
Passo 3
Aplicando a equação de Bernoulli entre os pontos (1) e (2):
Se liga: Nesse caso, estamos aplicando a equação de Bernoulli em dois pontos do mesmo fluido.
Por isso temos uma mesma densidade nos dois lados da igualdade. É bom ficar atento pois, como existe outro fluido na questão, você pode acabar se confundindo.
Passo 4
Hipótese: como o escoamento é horizontal, desconsideramos diferença de alturas:
Logo:
Passo 5
Rearranjando:
Vamos lembrar que e estão relacionadas pela equação da continuidade:
Passo 6
Substituindo:
Passo 7
Isolando :
Agora, note que não conhecemos ainda .
Para isso, aplicamos o Princípio de Stevin no manômetro em “U”.
Passo 8
Aplicando Princípio de Stevin nos pontos (A) e (B):
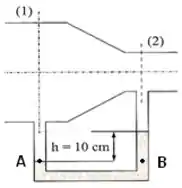
onde é a densidade do mercúrio e é a altura da coluna de mercúrio.
Pela figura:
Agora é só substituir os valores para determinar .
Passo 9
Substituindo valores:
Passo 10
Substituindo na equação anterior, para encontrar :
Passo 11
Agora podemos substituir para encontrar a vazão:
Resposta
Exercício Resolvido #3
UFRJ-P1-2013.1-D2
O medidor de Venturi é usado para se obter a velocidade de escoamento estacionário de um fluido não viscoso em uma tubulação. Considere um fluido incompressível, de densidade , que escoa em uma tubulação com área ade seção transversal Na região de estrangulamento, a área é reduzida pra , e um tubo manométrico é instalado como mostrado abaixo (vide figura). Suponha que o liquido do manômetro também seja incompressível e tenha densidade . NÃO despreze termos como
- Obtenha a diferença de pressão entre os pontos 1 e 2 em termos dos dados e da velocidade no ponto 1
- Determine a altura lida no medidor em função da diferença de pressão entre os pontos 1 e 2.
- Determine a velocidade de escoamento em termos dos dados do problema e das respostas anteriores.
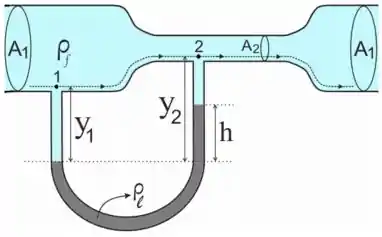
Passo 1
a)
Aqui a gente vai ter que aplicar Bernoulli entre os pontos 1 e 2.
Quando a gente usa Bernoulli, a gente precisa definir um ponto de altura
O ponto que usamos já tá definido ali na figura, é o nível que saem as alturas e
Ok, então o resto é só aplicar os valores de pressão altura e velocidade:
Beleza? Só que a gente não sabe . Então precisamos usar a equação da continuidade, certo?
Então:
Pronto (:
Passo 2
b)
A gente vai usar o principio de Stevin pra resolver isso. No nível de altura , as pressões são iguais pois tem a mesma altura. Então a pressão do lado esquerdo é a mesma que do lado direito:
A pressão do lado esquerdo vale:
OU seja, é a soma da pressão 1 mais a pressão devido a coluna de líquido azul.
Preste atenção nisso, pois temos dois fluidos ali.
E a pressão do lado direito vale:
Ou seja, é a soma da pressão 2, mais a pressão causada pela coluna de fluido e a coluna de fluido de liquido
A altura da coluna de liquido é (veja na figura).
A altura da coluna de é
Passo 3
Vamos igualar as duas:
Passo 4
c)
Temos duas expressões pra e uma delas tem . Vamos igualar as duas:
Resposta
a)
b)
c)
Exercício Resolvido #4
UFRJ-P1-2014.1-D1
Considere o encanamento abaixo, por onde corre horizontalmente, em regime estacionário, um fluido não viscoso de densidade . A extremidade do cano vertical está aberta para a atmosfera e a coluna de líquido nele contida não cai.
Considere conhecidas a pressão , a seção reta e a velocidade no ponto , a altura do cano vertical, a gravidade e a pressão atmosférica .
- Quais a velocidade e a pressão do fluido no ponto em função da seção reta no ponto ?
- Discuta o sinal de a partir das expressões obtidas no item anterior.
- Qual o valor de para que a coluna vertical de líquido não caia?
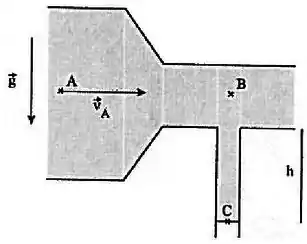
Passo 1
Resolvendo item (a):
Queremos a velocidade e pressão no ponto . O enunciado nos diz que a seção reta em é .
Isso tem cara de equação da continuidade e equação de Bernoulli.
Aplicando a equação da continuidade entre os pontos e :
Passo 2
Aplicando equação de Bernoulli entre os pontos e :
Como , podemos eliminar o último termo de cada lado, pois são iguais:
A pressão e a velocidade foram dadas e podemos substituir pelo que encontramos:
Passo 3
Resolvendo item (b):
Pelo que acabamos de calcular:
Multiplicando por nos dois lados:
Logo:
Passo 4
Vamos analisar o sinal dessa expressão.
Para isso, basta analisarmos o termo entre colchetes, pois e são sempre positivos.
Sabemos, pela figura, que
Logo:
Ao quadrado:
Logo, o termo entre colchetes também é positivo.
Então é positivo!
Passo 5
Resolvendo item (c):
Se você achou estranho essa coluna de líquido “flutuando”, saiba que não foi só você que achou isso!
Mas o fato é que, se essa coluna está parada, vale a equação da hidrostática:
Olhando para a coluna de líquido, sabemos que, no fundo da coluna, a pressão é , a pressão no topo é e a profundidade é .
Logo:
Se isso não te convenceu, podemos fazer de outra maneira.
Passo 6
Se você entendeu o passo anterior, pode pular para o passo 7!
Como essa coluna está parada, então a soma das forças que atuam nela é zero!
Fazendo o diagrama de corpo livre na coluna de líquido:
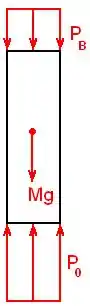
Note que, na parte superior da coluna, temos a pressão aplicada na área superior; e, na parte inferior, temos a pressão atmosférica atuando na área inferior.
Além disso, temos o peso da coluna de líquido.
Lembrando que pressão é força sobre área, podemos calcular as forças nas extremidades da coluna de líquido, multiplicando as pressões e pela área, que podemos chamar de :
Além disso, o peso é calculado como , sendo a massa total do líquido.
Pela figura, a força aponta para baixo e a força aponta para cima.
Somando as forças e igualando a zero:
Nós não sabemos o valor da área da coluna de líquido, nem a massa , mas sabendo sua altura .
Lembrando que volume é área vezes altura, podemos eliminar essa área da equação substituindo pelo produto da densidade pelo volume:
Mas , então:
Substituindo na equação:
Cancelando :
Uau! Que volta! Mas o resultado é o mesmo. Te convenci?
Passo 7
Agora é só substituir na equação que encontramos:
Mas o que queremos mesmo?
Ah, sim! A área . Então vamos isolar :
Multiplicando por os dois Laos:
Pronto! Esse monstrinho é o que procurávamos!
Resposta
Exercício Resolvido #5
Elaboração própria
Uma torneira aberta deixa vazar água continuamente em regime permanente. Considere que a água é um fluido incompressível.
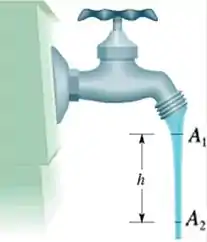
Nota-se que o filete de água vai se estreitando. Por que isso acontece?
Passo 1
Temos um escoamento em regime permanente. Neste caso, podemos usar a equação de continuidade:
Como estamos considerando a água incompressível:
Então nossa equação da continuidade fica assim:
Passo 2
Agora podemos explicar por que o filete de água estreita.
Sabemos que deve obedecer à equação da continuidade:
Como a água está caindo, ela está ganhando velocidade.
Por quê?
Porque, saindo da torneira, a água tem energia potencial (altura) que vai se convertendo em energia cinética (velocidade). Ou seja: por conservação de energia, a água ganha velocidade.
Logo:
Passo 3
Vamos rearrumar a nossa equação da continuidade:
Como :
Ou, em outras palavras:
Pronto! Como a velocidade aumenta, a área necessariamente tem que diminuir para manter a vazão constante, isto é, para obedecer à equação de continuidade:
Resposta
Como a velocidade aumenta, pela transformação de energia potencial mecânica em cinética, a área transversal necessariamente diminui à mesma proporção, para satisfazer a equação de continuidade.
Exercício Resolvido #6
PUCRIO-P1-2012.1-Q3
A figura abaixo mostra um garrafão de água mineral, hermeticamente fechado, que se encontra cheio até uma altura acima da boca da torneira. A área da boca da torneira é de (), muito menor do que a área da superfície da água dentro do garrafão. O ar acima da superfície da água está a uma pressão menor do que a pressão atmosférica, pressão manométrica . Considere o escoamento ideal, a aceleração da gravidade e .

- Determine a velocidade com que o fluido escoa.
- Calcule a vazão da torneira e determine o tempo necessário para se encher um copo de (volume igual a ).
- Ao sair da torneira, o jato de água fica mais fino durante a queda. Determine a área do jato após cair de uma altura abaixo da boca da torneira.
Passo 1
a)
Vamos calcular a velocidade de escoamento após o fluido percorrer a altura do garrafão.
Vamos usar a equação de Bernoulli:
Sendo que , , , e
Pra encontramos precisamos usar a definição de pressão manométrica:
Logo:
Então, a equação de Bernoulli fica:
Passo 2
b)
Como a gente já tem a velocidade, fica fácil calcular a vazão, já que vazão é velocidade vezes a área:
E essa é a taxa de variação do volume. Pra descobrirmos o tempo necessário pra se encher o copo, podemos usar a relação:
Passo 3
c)
Aqui iremos usar o princípio da continuidade:
O que acontece nessa situação? Bom, enquanto o fluido vai caindo, a sua velocidade vai aumentando. Como o princípio da continuidade deve ser respeitado, o aumento da velocidade gera uma diminuição da área.
Bom, então vamos calcular a velocidade do fluido quando .:
Vamos aplicar Bernoulli entre o ponto da torneira e o ponto de altura .
Vamos aplicar, então, Bernoulli entre a torneira e o ponto de altura . Vamos considerar, então, o ponto da torneira como ( E é por isso como que colocamos a outra altura como negativa).
Então, vamos usar agora aquela equação do início:
Resposta
a)
b)
c)
Exercício Resolvido #7
UFRJ-P1-2014.2-D2
A água sai de uma torneira aberta de forma a formar um feixe que se afina, sem se dividir, conforme a água flui em direção ao ralo, como indica a figura. Supondo que a seção transversal deste feixe se mantém circular no decorrer do fluxo, com raio e velocidade da água imediatamente após sair da torneira, e considerando a água um fluido incompressível sem viscosidade (considere a aceleração da gravidade conhecida), estime:
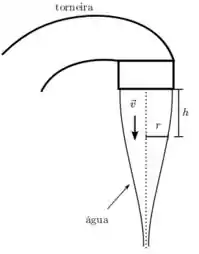
- A velocidade do fluido , em função da diferença de altura a partir da torneira.
- O raio de seção transversal do feixe, em função do módulo de velocidade nesta seção do fluido.
- O raio de uma seção transversal de um feixe, , agora em função da diferença de altura a partir da torneira.
Passo 1
a)Vamos usar Bernoulli aqui!
Vamos fazer assim: O ponto de altura zero será o ponto onde as moléculas do fluido terão uma velocidade . A altura cresce de baixo pra cima.
Então, calculando entre esse ponto e o ponto da boca da torneira:
Passo 2
b)
Aqui a gente usa o principio da continuidade, ou seja:
Vamos tomar como a vazão que a gente calcula bem na boca da torneira. Como ela tem raio
Então:
A outra vazão é calculada pelo produto da área da seção que vai diminuindo( pela velocidade . Então:
Igualando as duas:
Passo 3
c)
Po, bem tranquila essa. Já temos a equação da velocidade em função da altura em a), basta a gente substituir na equação encontrada em b):
Resposta
a)
b)
c)
Exercício Resolvido #8
Hugh D. Young e Roger A. Freedman, Física II – Termodinâmica e Ondas, 12a ed. São Paulo: Addison Wesley, 2008, pp 100 – Modificado
A água de uma grande tanque aberto com paredes verticais possui uma profundidade ( figura abaixo). Um orifício é aberto na parede vertical a uma profundidade abaixo da superfície da água.
- Qual é a distância entre a base do tanque e o ponto onde a corrente atinge o solo?
- Qual a distância acima da base do tanque devemos fazer um segundo furo para que a corrente que emerge dele tenha um alcance que igual ao do primeiro furo?
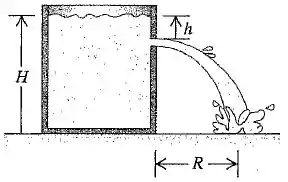
Passo 1
a)
Bom, o que você precisa fazer primeiro aqui?
Você precisa, primeiro, calcular a velocidade do esguicho de água. Como a gente viu na teoria, vamos tomar o ponto na superfície da água e ponto na saída do jato.
Passo 2
Assim:
Beleza. Agora precisamos achar a distância horizontal que esse jato percorre antes de atingir o solo.
Pra issoo, vamos ter que primeiro achar o tempo de queda.
Esse jato cai da seguinte altura:
Como a velocidade vertical inicial é nula, podemos usar a fórmula:
A distância horizontal percorrida vai ser esse tempo vezes a velocidade achada:
Passo 3
b)
Agora nós vamos pegar uma distância em relação à base do tanque. Vamos chamá-la de
Como a medida vai ser a altura do jato, o tempo de queda livre vai ser dado por:
Como nós fizemos no caso anterior.
Já a altura em relação à superfície vai ser dada por:
Assim, a velocidade do jato vai ser:
Assim, a distância horizontal será:
Fazendo
Comparando, percebemos que:
Ou seja, pra se ter a mesma distância, basta pegar a mesma altura , só que agora sendo medida a partir da base.
Resposta
a)
b)
Exercício Resolvido #9
UNICAMP-Questão 4P1-2010
Considere um grande reservatório contendo um líquido de massa específica . Suponha que a altura do líquido seja e que é feito um furo pequeno no reservatório a da altura , conforme mostra a figura. Saindo pelo orifício, o líquido atinge uma distância da base do reservatório.
a) Calcule essa distância .
b) Calcule a altura de um segundo furo feito abaixo do primeiro e tal que o alcance do líquido saindo dele seja igual ao do primeiro. Para os seus cálculos, suponha que o nível do reservatório não se altera durante todo o processo.
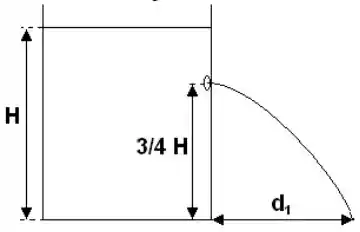
Passo 1
a)
Vamos aplicar Bernoulli entre a superfície do fluido e o ponto onde há o fluido, usando o nível do chão como o nível zero de referência.
E essa é a velocidade com que o fluido sai pelo orifício. Agora vamos dar uma lembrada de Física 1( Caso não se lembre, acesse o nosso material de Física 1):
O tempo de queda de um corpo submetido a uma altura e sujeito à uma gravidade é:
Como
Então a distância será:
Passo 2
b)
Vamos chamar de a distância da superfície até o ponto que queremos achar. Logo, a altura que a gente procura vai ser . Aplicando Bernoulli entre o ponto do furo e a superfície:
O tempo de queda do fluido será:
Logo:
Comparando esse resultado com
Resolvendo essa equação, encontramos:
O caso corresponde ao caso do enunciado, pois ai a altura fica: . Então a gente deve usar :
Pronto (:.
Resposta
a)
b)
Exercício Resolvido #10
UERJ-LISTA-MF-19
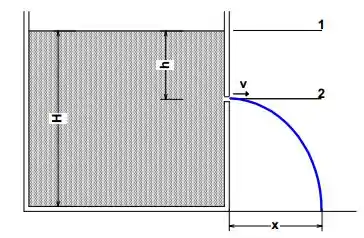
Um tanque contém água até uma altura . É feito um pequeno orifício na sua parede à profundidade da superfície, conforme a figura.
Mostre que a distância da base da parede até onde o jato atinge o solo é dada por .
Calcule a profundidade do buraco para que o jato emergente atinja o solo a uma distância máxima da base do tanque.
Passo 1
Primeiramente: Vamos analisar o problema sob a ótica da equação de Bernoulli, comparando o nível 1 ao nível 2 do fluído (conforme a figura). Dessa forma, vamos conseguir obter a velocidade do fluido no nível 2, o que permitirá resolver o resto da questão. Vamos obter as informações necessárias de cada nível:
Nível 1:
Altura da coluna de líquido: (a superfície é estática)
Nível2:
Altura da coluna de líquido:
Vamos equacionar agora:
Como , podemos cortar as pressões em ambos os lados da equação. Nesse ponto, a gente costuma ficar em dúvida sobre o por quê da pressão no ponto 2 ser a pressão atmosférica, e não a pressão hidrostática causada pela coluna de líquido de altura ....
Bom, a resposta é simples: Estamos considerando um ponto que está na iminência de sair do tanque e não exatamente dentro do tanque! Ou seja, é como se estivéssemos analisando um ponto que já está fora do tanque e, por isso, sujeito a pressão atmosférica do lado de fora!
Continuando...
Com esse valor, agora vamos poder resolver os itens e (:
Passo 2
Nos passos seguintes, nós vamos usar conceitos de cinemática. O movimento do fluído após sair pelo orifício, no nível 2, é obliquo. Bom, a velocidade é puramente horizontal, já que o fluido é expelido perpendicularmente à parede do tanque! Logo, a distância pode ser expressa por:
(eq.1)
No qual é o tempo de queda do fluido.
Bom, como a altura que as partículas do fluido vão percorrer é (olhe a figura),e o movimento na vertical em um lançamento obliquo é um ,é possível escrever:
Isolando
Substituindo o valor de e na eq.1:
Pronto, essa demonstração é a solução da (:
Passo 3
Vamos para a letra
Precisamos achar uma altura tal que a distância seja máxima. Bem, utilizaremos aquele velho conceito de máximos e mínimos de funções de uma variável de cálculo. Podemos considerar a relação encontrada anteriormente de , ou seja, uma função de
No entanto, é fácil perceber que essa função terá um máximo quando a expressão tiver um máximo. Fazendo , vamos encontrar o máximo dessa função, que é do segundo grau. Derivando em relação a :
Igualando a zero:
Pronto, essa é a resposta da letra (:
Resposta
Exercício Resolvido #11
UNICAMP, Questão 4 P1-2010
Um sifão é usado para retirar líquido de um reservatório através de um tubo recurvado e fazendo jorrar água () em , como mostra a figura. A área do reservatório é muito maior do que a área da secção transversal do tubo; considere o fluido ideal e use e ,
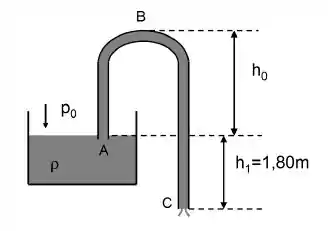
- Calcule a velocidade de escoamento em .
- Qual é o valor máximo de para o qual o sifão ainda funciona?
Passo 1
a) Bom galera, vamos considerar que o nível de altura nula passa pelo ponto c. Dessa forma, o ponto c tem altura igual a zero.
Vamos agora aplicar Bernoulli entre e
Vamos às características de cada ponto:
A altura de do ponto foi medido em relação ao nível de altura nula, por isso esse valor. O valor da velocidade do fluido em tende a zero, já que o fluido começa a subir o tubo ali, e, somente a partir dali ele começa a ganhar velocidade.
Mas por quê o valor da pressão de é igual ao valor da pressão atmosférica?
Porque, como a velocidade ali é nula, estamos no regime da hidrostática. Ou seja...,podemos aplicar Stevin!
Isso quer dizer que o valor da pressão de é igual ao valor da pressão do ponto do fluido logo ao lado, fora do cano, já que ambos possuem a mesma altura. E o valor da pressão na superfície do fluido é
O que queremos saber.
Bem, a altura é zero pois o referencial de altura nula está passando por . A pressão é a pressão atmosférica pois o cano está aberto pra atmosfera.
Por Bernoulli:
Passo 2
b)
O valor máximo vai ocorrer quando a pressão de for nula.
Mas como vamos calcular a pressão de ?
Oras, bora comparar o ponto ao ponto , usando Bernoulli:
Pela a equação da continuidade, temos que:
E lembrando que:
Assim:
Logo, pra
Pronto, o valor máximo é:
Resposta
a)
b)
Exercício Resolvido #12
UNICAMP Questão 4 - P1.2012
A figura mostra um sifão, que é um tubo usado para transferir líquidos de um recipiente para outro. O tubo deve estar inicialmente cheio, e se esta condição é satisfeita o líquido escoa pelo tubo até que a superfície do líquido no recipiente esteja no mesmo nível que a extremidade . O líquido tem densidade igual a e viscosidade desprezível. As distâncias mostradas na figura são , e . Considere .
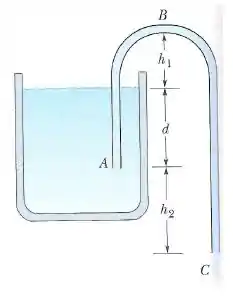
- Com que velocidade o líquido sai do tubo no ponto ?
- Se a pressão atmosférica é , qual é a pressão do líquido no ponto , o ponto mais alto do tubo?
- Qual é o máximo valor de , mantidos e , para que o líquido continue escoando?
Passo 1
a)
Bom galera, vamos considerar que o nível de altura nula passa pelo ponto c. Dessa forma, o ponto c tem altura igual a zero.
Vamos agora aplicar Bernoulli entre e o ponto logo acima de na superfície do fluido(Vamos chamá-lo de :
Vamos às características de cada ponto:
A altura de do ponto foi medido em relação ao nível de altura nula, por isso esse valor. O valor da velocidade do fluido em tende a zero, já que o fluido começa a subir o tubo ali, e, somente a partir dali ele começa a ganhar velocidade.
Mas por que o valor da pressão de é igual ao valor da pressão atmosférica?
Porque, como a velocidade ali é nula, estamos no regime da hidrostática. Ou seja...,podemos aplicar Stevin!
Isso quer dizer que o valor da pressão de é igual ao valor da pressão do ponto do fluido logo ao lado, fora do cano, já que ambos possuem a mesma altura. E o valor da pressão na superfície do fluido é
O que queremos saber.
Bem, a altura é zero pois o referencial de altura nula está passando por . A pressão é a pressão atmosférica pois o cano está aberto pra atmosfera.
Por Bernoulli:
Passo 2
b)
Pra descobrir a pressão no ponto , vamos analisar a pressão no ponto
Ou seja, a pressão no ponto é igual a pressão no potno mais a pressão devida à altura da coluna de fluido.
Essa altura é:
Logo:
Sendo :
Logo:
Passo 3
c)
O valor máximo vai ocorrer quando a pressão de for nula.
Usando a equação do item anterior:
Resposta
a)
b)
c)
Exercício Resolvido #13
UFRJ-Discursiva 1 - P1.2015
Dois tanques abertos estão cheios de um mesmo fluido de densidade constante, como ilustrado na figura. Um tubo horizontal tem uma extremidade conectada ao fundo do primeiro tanque e outra extremidade aberta, de modo que o fluido pode escoar para fora do tanque. O tubo possui um estrangulamento () onde a área da seção reta é a metade da área nas extremidades ( e ). Conectamos com um tubo em U o estrangulamento ao segundo tanque, de modo que a extremidade do tubo fica imersa no fluido. Com isso uma coluna de fluido preenche o tubo até uma a altura , após atingido o equilíbrio. Considere que a densidade do ar entre os pontos e é suficientemente pequena para desprezarmos variações de pressão com a altura. Considere também que as áreas das superfícies de fluido nos dois tanques são muito maiores que as das seções retas do tubo horizontal, que o escoamento do fluido através do mesmo é estacionário e que a aceleração da gravidade e a pressão atmosférica são constantes e conhecidas em todos os pontos da figura.
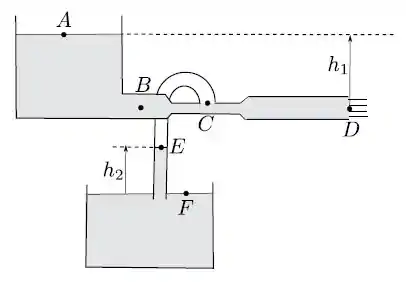
- Calcule a velocidade de escoamento do fluido no ponto indicado na figura.
- Calcule a velocidade do escoamento no ponto .
- Calcule a pressão manométrica (diferença entre a pressão absoluta e a pressão atmosférica) no ponto .
- Calcule a altura da coluna de fluido em termos da altura .
Passo 1
a)
Aqui a gente pode aplicar Bernoulli entre os pontos A e D. Lembrando que ,na superfície de um tanque com dimensões muito maiores que as dimensões dos encanamentos, podemos desprezar a velocidade do fluido.
Assim:
Vamos considerar como o nível zero de altura o nível do ponto D. Logo, tem altura zero e tem altura . Como ambos os pontos estão abertos pra atmosfera, a pressão dos dois é igual à pressão atmosférica, que vamos chamar de Logo:
Passo 2
b)
Se a gente sabe a velocidade no ponto e a relação entre as áreas das seções transversais no ponto e , a gente pode aplicar a equação da continuidade entre os pontos.
Então, como a vazão se conserva, temos:
Só que o enunciado nos diz que a área de é a metade da área de , logo:
Passo 3
c)
A gente pode escolher aplicar Bernoulli entre e ou entre e . Vamos escolher entre e
Aplicando:
Repare que não colocamos as energias das alturas porque são iguais ( mesma altura).
A gente já descobriu essas duas velocidades e a pressão em , então:
Mas a gente quer a diferença dessa pressão com a pressão atmosférica ( logo:
Passo 4
d)
Agora nós queremos achar o valor de . Essa é a opção mais difícil. Vamos esquecer um pouco de Bernoulli aqui e lembrar de stevin.
A coluna de líquido de altura está em equilíbrio. Isso quer dizer a soma da pressão do ponto E mais a pressão exercida pela coluna de líquido tem que ser igual à pressão atmosférica. Por quê? Bom, a pressão atmosférica empurra a coluna de fluido de baixo pra cima, assim como as outras duas pressões empurram de cima pra baixo. Elas precisam ser iguais pra que o sistema entre em equilíbrio, pois se não fossem, haveria uma força resultante e não haveria equilíbrio.
Vamos lá:
Só que como o sistema está em equilíbrio, a pressão em tem que ser a mesma que em . Perceba que os pontos estão ligados apenas por um cano com ar. Como o ar está parado, ele apenas comunica a pressão de um ponto ao outro. Logo:
Resposta
a)
b)
c)
d)