Equação da Continuidade
Produzido por Leonardo de BemTeoria
Olá galera bonita, nós somos o Responde Aí, a plataforma de exatas que vai ajudar você a mandar super bem nas suas provas!
Então, partiu aprender com o Responde Aí a equação da continuidade? 👊🏾
Equação da Continuidade
A primeira coisa que precisamos entender é que a equação da continuidade surge do princípio da conservação de massa.
Vamos imaginar um fluido escoando no interior de um tubo, como mostra a figura:
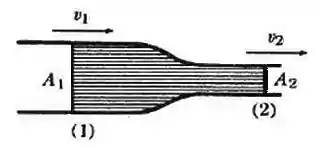
Depois de um certo tempo, uma quantidade de massa entra no ponto
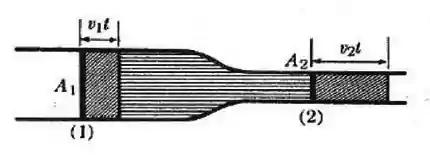
É aqui que entra a conservação de massa, que nos diz que massa não pode ser criada e nem destruída, ou seja, a quantidade de massa que entra no ponto
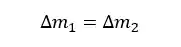
Se considerarmos um intervalo de tempo
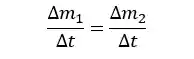
Agora, para chegarmos na equação da continuidade, precisamos escrever essa relação da variação de massa nos dois ponto em função de grandezas que nós conhecemos em um escoamento, como a velocidade
Note que se multiplicarmos a área transversal em um ponto,
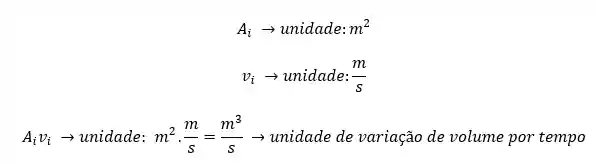
Agora, para passarmos essa variação de volume por tempo para variação de massa, basta multiplicarmos pela densidade do fluido:
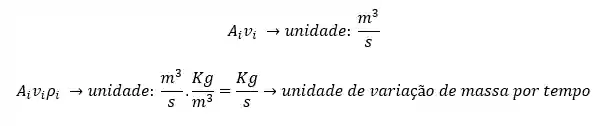
Sendo assim, podemos reescrever a equação da conservação da variação de massa em termos dessas três grandezas mencionados anteriormente e obtemos como resposta a tão famosa equação da continuidade:
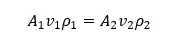
Equação da Continuidade para Fluidos Incompressíveis
Um fluido é dito incompressível quando a sua densidade é constante. Olhando para a equação da continuidade, um fluido ser incompressível quer dizer que a densidade no ponto
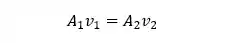
E é essa a equação da continuidade. Curtiu?
A partir de agora você pode exercitar bastante esse conceito fazendo exercícios, que você encontra na nessa nossa página aqui: Equação da Continuidade - Exercícios. Você pode também partir para o próximo tópico e avançar nos estudos, é só conferir essa página aqui: Equação de Bernoulli. Ou, você pode também fixar ainda mais a equação da continuidade assistindo esse conteúdo em vídeo, que eu vou deixar aqui embaixo 👇🏾