Pressão Hidrostática
Produzido por Leonardo de BemTeoria
Fala aí, nós somos o Responde Aí, tudo que você precisa para aprender as matérias de forma clara, descontraída e direto ao ponto e arrebentar nas provas.
Hoje vamos ter uma conversa sobre a pressão hidrostática.
A pressão hidrostática nada mais é que a pressão que uma coluna de líquido exerce em uma determinada profundidade.
Então, vamos imaginar que você mergulhou no mar e está a uma profundidade
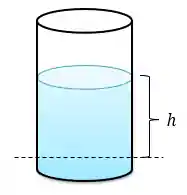
A pressão hidrostática é proporcional à densidade do líquido, à aceleração da gravidade local e à altura do líquido acima do ponto considerado. Desse modo, a pressão hidrostática é calculada da seguinte forma:
Onde:
é a densidade do fluido, em ; é a celeração da gravidade, que vale ; é a altura do líquido acima do ponto considerado, em , e; é a pressão hidrostática, em
Essa é a pressão exercida apenas pela coluna de líquido acima do ponto, mas e se acima da coluna de líquido houver alguma pressão atuando também, como é o caso do mar, acima do nosso exemplo, porque acima do mar temos a pressão atmosférica atuando então a pressão total,
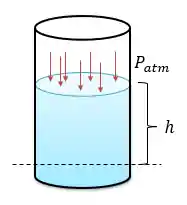
Importante: A pressão atmosférica vale
Mas, nem sempre a pressão que atua acima do líquido é a pressão atmosférica, pode ser a pressão exercida por um gás dentro de um recipiente por exemplo, então vamos generalizar e chamar a pressão que atua acima da coluna de líquido de
Tem mais uma coisa bem legal sobre a pressão hidrostática pra te falar.
Olha essa imagem aqui:

Ambos os recipientes estão preenchidos por uma mesmo fluido, até uma mesma altura. A pressão hidrostática no fundo dos recipientes vai ser igual ou diferente?
A pressão hidrostática será exatamente igual. Isso porque vimos que a pressão hidrostática depende da densidade do fluido, da altura da coluna de fluido e da gravidade, que sempre será a mesma no nosso caso, e não do formato do recipiente. Então, se temos esses cincos recipientes preenchidos pelo mesmo fluido (densidade são iguais) até uma mesma altura, a pressão hidrostática no fundo será exatamente a mesma, não importando o formato do recipiente.
Em outras palavras, a fórmula
Exemplo
Aqui no Responde Aí, nós temos vários vídeos de exercícios que mostram como resolver passo-a-passo. Eu vou deixar um exercício aqui em vídeo pra você ver como esse conteúdo é abordado nas questões e para você conhecer um pouquinho mais do nosso estilo. Confere aí:
Exercícios Resolvidos
Exercício Resolvido #1
Lista de exercícios, Fenômenos de transporte, UERJ
A figura mostra três vasos , e cujas bases tem a mesma área. Os vasos estão cheios de líquido , e até uma mesma altura. As pressões nos fundos dos vasos são , e , respectivamente. Com relação a essa situação, é correto afirmar que:
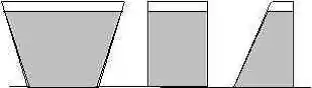
- somente se os líquidos , e forem idênticos.
- quaisquer que sejam os líquidos , e .
- somente se os líquidos , e forem idênticos.
- quaisquer que sejam os líquidos , e .
Passo 1
Pelo paradoxo hidrostático, sabemos que a pressão no fundo dos vasos exercida pelo fluido não depende da forma do recipiente, apenas da densidade do fluido, gravidade e profundidade:
Passo 2
Pela figura, a profundidade é a mesma em todos os casos, assim como a aceleração da gravidade .
O que vai definir se as pressões serão iguais ou não é se as densidades dos fluidos são iguais ou não.
Logo, se tivermos o mesmo fluido nos três casos, temos densidades idênticas nos três casos.
Se isso acontecer, teremos a mesma pressão nos três casos!
Alternativa (a).
Resposta
Alternativa (a).
Exercício Resolvido #2
Halliday, Vol 2, Capítulo 14, 9ª edição, exercício 8, página 80.
Embolia gasosa em viagens de avião. Os mergulhadores são aconselhdados a não viajar de avião nas primeiras 24h após um mergulho porque o ar pressurizado usado durante o mergulho pode introduzir nitrogênio na corrente sanguínea. Uma redução súbita da pressão do ar (como a que acontece quando um avião decola) pode fazer com que o nitrogênio forme bolhas no sangue, que podem produzir embolias dolorosas ou mesmo fatais. Qual é a variação de pressão experimentada por um soldado da divisão de operações especiais que mergulha a de profundidade em um dia e salta de paraquedas de uma altitude de no dia seguinte? Suponha que a massa específica média do ar nessa faixa de altitude é .
Dados:
Passo 1
O problema quer saber o quanto a pressão variou de um evento para outro.
Vamos chamar de a pressão dentro da água (no mergulho) e de a pressão quando saltando de paraquedas.
Além disso, vamos chamar de a pressão atmosférica no nível do mar.
Nós vamos ter:
Repare que a pressão na região em que o soldado salta de paraquedas é igual à pressão ao nível do mar (atmosférica) menos a pressão da camada de ar numa altura de .
Então o que queremos encontrar será:
Onde é a densidade média do fluido, é a aceleração da gravidade e é a distância vertical para o ponto onde a pressão é igual à pressão atmosférica.
Passo 2
Substituindo:
Resposta
A variação de pressão experimentada pelo soldado é .
Exercício Resolvido #3
Hugh D. Young e Roger A. Freedman, Física II – Termodinâmica e Ondas, 12a ed. São Paulo: Addison Wesley, 2008, pp 94 – Modificado.
Os cientistas encontraram indícios de que Marte pode ter tido outrora um oceano com de profundidade. A aceleração da gravidade em Marte é .
- Qual seria a pressão manométrica no fundo desse oceano?
- A que profundidade você precisaria descer nos oceanos da Terra para ser submetido à mesma pressão manométrica?
Dados necessários:
Densidade da água do mar: .
Aceleração da gravidade na Terra: .
Passo 1
a)
Bom, ele está pedindo a pressão manométrica no fundo do oceano. Você lembra o que isso significa?
Isso mesmo, nesse caso, vai ser a pressão da coluna de água. Se ele pedisse a pressão absoluta, você deveria somar a pressão da coluna de água com a pressão atmosférica do planeta.
Vamos lá, então é só usar a famosa fórmula vista na teoria:
Lembre-se: aqui vamos usar a profundidade do oceano de marte, , a densidade da água do mar e a gravidade de marte.
Então:
Beleza? (:
Passo 2
b)
Agora ele quer que você descubra a profundidade de um suposto oceano na Terra que gere a mesma pressão manométrica. O que vai mudar? Isso aí, a gravidade!
Ah, mas e a densidade, muda? Bom, como o enunciado não disse nada em relação a isso, vamos considerar a mesma densidade. E é claro, vamos usar a mesma pressão manométrica do oceano marciano.
Passo 3
Assim:
Não usamos a pressão atmosférica em nenhum lugar porque estamos usando o conceito de pressão manométrica, viu?
Resposta
Exercício Resolvido #4
Halliday, Vol 2, Capítulo 14, 9ª edição, exercício 12, página 80
A profundidade máxima a que um mergulhador pode descer com um snorkel (tubo de respiração) é determinada pela massa específica da água e pelo fato de que os pulmões humanos não funcionam com uma diferença de pressão (entre o interior e o exterior da cavidade torácica) maior que . Qual é a diferença entre os valores de , para água doce e para a água do mar Morto (a água natural mais salgada no mundo com uma massa específica de )?
Dados:
Passo 1
Cara, queremos uma diferença entre duas profundidades em uma determinada pressão. E como podemos calcular a pressão? Temos uma fórmula pra nos ajudar:
Beleza!! Então, vamos usá-la pra calcular as profundidades em cada situação e calcular a diferença entre elas depois.
Passo 2
Queremos saber a diferença de profundidade nas águas numa situação em que a pressão vale .
Então, na água doce: . E a profundidade máxima será:
No mar Morto: . E a profundidade máxima será:
Passo 3
Calculando a diferença entre os :
Resposta
A diferença entre os valores de vale .
Exercício Resolvido #5
Halliday, Vol 2, Capítulo 14, 9ª edição, exercício 17, página 80
Alguns membros da tripulação tentam escapar de um submarino avariado abaixo da superfície. Que força deve ser aplicada a uma escotilha de emergência, de por ,
para abri-la para fora nessa profundidade? Suponha que a massa específica da água do oceano é e que a pressão do ar no interior do submarino é .
Passo 1
Primeiro vamos entender a situação das forças agindo na escotilha do submarino:
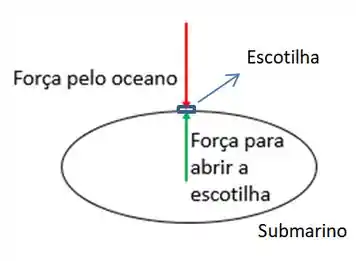
Repare que não precisamos considerar a pressão interna de . Por quê? Porque no nível do mar também existe uma pressão atmosférica igual à pressão interna do submarino. Então na real, a diferença entre as pressões interna e externa é só a pressão hidrostática mesmo.
Então, para abrir a escotilha, só precisamos que a força para abri-la seja maior que a força pelo oceano. No caso, a força do oceano é uma força devido à pressão hidrostática da água numa profundidade de . E como podemos achar essa força? Usando:
Onde a pressão pode ser calculada por:
E:
Substituindo na equação da força:
Resposta
A força aplicada deve ser .
Exercício Resolvido #6
Hugh D. Young e Roger A. Freedman, Física II – Termodinâmica e Ondas, 12a ed. São Paulo: Addison Wesley, 2008, pp 94 – Modificado.
Você está projetando um sino de mergulho pra aguentar a pressão da água do mar até uma profundidade de
a) Qual é a pressão manométrica nessa profundidade? (Despreze as variações de densidade da água com a profundidade).
b) Levando-se em consideração a pressão da coluna de líquido e a pressão atmosférica, qual é a força resultante exercida pela água fora do sino e pelo ar dentro do sino sobre uma janela de vidro circular com diâmetro de ? (Despreze a pequena variação de pressão sobre a superfície da janela).
Dados necessários:
Passo 1
a)
Bom, galera, novamente a questão está pedindo a pressão manométrica.
O que isso significa? Que vamos calcular a pressão que a coluna de líquido exerce (e não somaremos com a pressão atmosférica).
Então usaremos a fórmula:
Lembrando que só podemos usar a fórmula porque a densidade não varia.
Aqui você precisa ter cuidado com as dimensões. Use as mesmas dimensões da densidade da água, ok? Como está no SI, vamos usar o SI.
Assim:
Passo 2
b)
Agora nós precisamos achar a força resultante numa janela naquela profundidade. Pra isso, devemos calcular a pressão do lado de fora e a pressão do lado de dentro do sino.
A pressão de dentro do sino é a pressão do ar que está ali dentro. Logo, a pressão atmosférica.
E a pressão do lado de fora é a pressão absoluta naquela profundidade. Ou seja:
Então, como é possível ver, a pressão do lado de fora vai ser maior. Assim, a força estará apontando para dentro do sino.
Passo 3
Pra calcular a força, precisamos primeiro calcular o diferencial de pressão. Assim:
Show?
Bom, e como a pressão é dada por:
Então:
Passo 4
Temos quase tudo, só falta calcular a área da janela circular. Bom, o diâmetro da janela é:
Assim, o raio será:
E a área será:
Assim:
Resposta
Exercício Resolvido #7
Hugh D. Young e Roger A. Freedman, Física II – Termodinâmica e Ondas, 12a ed. São Paulo: Addison Wesley, 2008, pp 94 – Modificado
Um barril contém uma camada de óleo de flutuando sobre água. A camada de água tem uma altura de . A densidade do óleo é igual a .
- Qual é a pressão manométrica na interface entre o óleo e a água?
- Qual é a pressão manométrica no fundo do barril?
Outros dados:
Passo 1
a)
Aqui temos o caso em que há dois fluidos diferentes em um mesmo recipiente.
O problema pede a pressão na interface dos dois líquidos.
Repare que, como ele pede a pressão manométrica, o que ele quer é a pressão naquele ponto menos a pressão atmosférica. Ou seja, o que ele quer é a pressão hidrostática, sacou?
Essa pressão vai ser a pressão da coluna de líquido que está acima da camada de água, ou seja, a pressão da camada de óleo.
Então:
E essa é a pressão na interface.
Passo 2
b)
Show, e agora? Agora precisamos achar a pressão no fundo do barril, ou seja, achar a pressão causada pelas duas colunas de fluido: a pressão causada pela coluna de água e a pressão causada pela coluna de óleo.
A gente já tem a pressão causada pelo óleo, agora basta calcular a causada pela água:
Passo 3
Show. Agora é só somar as duas pressões:
Isso é a pressão manométrica, porque a pressão absoluta incluiria a atmosférica.
Resposta
Exercício Resolvido #8
Hugh D. Young e Roger A. Freedman, Física II – Termodinâmica e Ondas, 12a ed. São Paulo: Addison Wesley, 2008, pp 94 – Modificado
Um cilindro alto com uma área de seção reta igual a está parcialmente cheio de mercúrio. A superfície do mercúrio está acima do fundo do cilindro. Despeja-se água lentamente sobre o mercúrio, e os dois fluidos não se misturam. Que volume de água deve ser acrescentado para dobrar a pressão manométrica no fundo do cilindro?
Dados:
Passo 1
Primeiramente, a gente precisa saber qual é a pressão manométrica do mercúrio no fundo do cilindro. Repara que a área de seção reta que ele falou é a área da base do cilindro.
Essa pressão pode ser calculada por:
Passo 2
Agora que sabemos a pressão inicial, , vamos dobrá-la:
Essa pressão tem que ser igual a pressão da coluna de mercúrio mais a pressão da camada de água que vamos jogar em cima desse mercúrio.
Assim:
Passo 3
Legal! Já sabemos a altura de água que vamos despejar. O que falta agora? Saber qual o volume de água correspondente. Pra isso, vamos multiplicar essa altura pela a área da seção transversal:
E é esse aí o volume despejado (: