Teoria
Agora vamos ver outro conceito importante no estudo dos fluidos: a pressão.
Dá uma olhada nesse tirinha:

Por que um afunda e o outro não?
Por mais que os dois homens tenham o mesmo peso, o peso do segundo está distribuído em uma área maior que a do primeiro. Então ele exerce menos pressão e não afunda!
O que é pressão, afinal? É a razão força sobre área:
Sacou? Basta perceber que a área e a pressão são inversamente proporcionais para uma mesma força.
Unidade
Mas qual a unidade de pressão no Sistema Internacional?
Força é medido em Newton, área em , então
Essa unidade leva o nome de Pascal:
Existem outras unidades de pressão que podem aparecer nos exercícios, mas em geral a conversão para Pascal será dada.
Por exemplo, o peso que a atmosfera da Terra exerce sobre sua superfície gera uma pressão chamada de pressão atmosférica, que seu valor é conhecido como 1 atm, onde:
Diferença de Pressão e Força
Por que o refri sobe quando você suga o canudinho?
Repare que a refri está sujeito a pressão atmosférica, assim como tudo que está na superfície da Terra.
Quando você suga, você está criando uma região de baixa pressão dentro da sua boca ().
Tanto a pressão atmosférica quanto a pressão baixa da boca vão gerar forças no líquido. A diferença de pressão vai gerar uma força resultante:
Onde ; e
A é a área da seção reta do canudo.
Se a força resultante for maior que o peso do refri, ele vai pra cima.
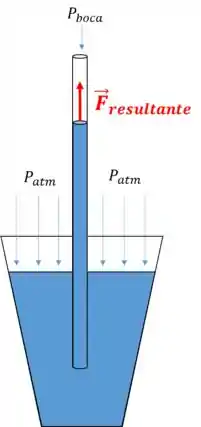
De forma geral, diferenças de pressão geram forças!
Forças Tangenciais e Normais
As forças que agem em um material podem ser divididas em dois componentes:
- Forças tangenciais: São as forças que agem paralelamente a superfície. São chamadas de forças de cisalhamento.
- Forças Normais: São as forças que são aplicadas na direção perpendicular à superfície. Elas comprimem o material e são elas as que geram pressão.
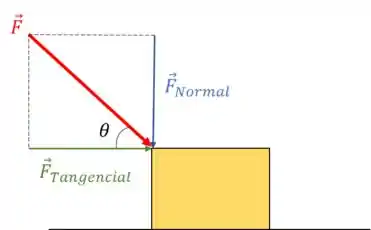
A pressão nesse bloquinho é:
Ah, mas e se a força não for constante ao longo de toda a área de contato?
Vamos ter que apelar para o cálculo e usar a forma diferencial:
Onde é um pedacinho infinitesimal de área do objeto e a força normal que age nele.
Mas fica tranquilo que isso é bem raro de aparecer. Na maioria das vezes, usamos apenas a expressão:
Legal! Isso é tudo o que você precisa saber antes de começar a estudar estática dos fluidos!
Partiu fazer uns exercícios?