Órbitas em Torno do Centro de Massa
Produzido por Ludovic BeghinTeoria
Vimos como se comporta um objeto que está orbitando ao redor de um objeto fixo, certo? Como podemos saber o comportamento de um par de objetos móveis? Vamos descobrir!
Mas antes vamos começar relembrando um conceito importante para esse assunto!
Cálculo do centro de massa
Vamos lembrar lá de sistema de partículas, quando já fizemos esse cálculo.
A primeira coisa a se fazer é definir um sistema de coordenadas. Para facilitar nem que seja um pouquinho a conta, coloque a origem em uma das massas. Se liga nessa imagem:
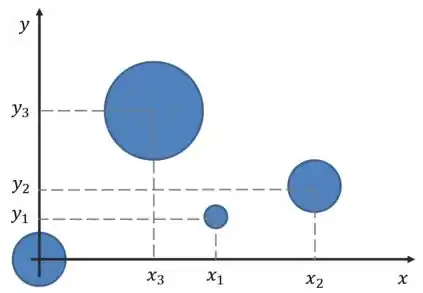
E o cálculo do centro de massa é basicamente uma média ponderada das coordenadas, tendo as massas como pesos, saca só:
Devido à nossa escolha de colocar uma das massas na origem (na imagem foi a massa número ), temos:
Raio da órbita
Considerando agora o par de massas, comumente chamado de binário, temos, após encontrar o centro de massa, o seguinte esquema:
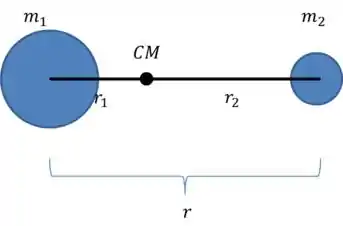
O que precisamos entender aqui é que ambas as massas vão orbitar o centro de massa! E então o raio da órbita de cada uma das massas e são, respectivamente, e .
Velocidade e período orbital
Agora chegamos no que pode ser cobrado nas questões!
Essas massas, apesar da estranheza do sistema, continuam realizando órbitas circulares ao redor do centro de massa. Antes de tudo, vamos encontrar uma expressão para e em função das massas e da distância entre elas.
Usando o que aprendemos para calcular o centro de massa, conseguimos:
Para encontrarmos a velocidade orbital, NÃO PODEMOS USAR A FÓRMULA ANTERIOR, dada por:
Portanto, vamos deduzir uma nova expressão, igualando novamente a força centrípeta à força gravitacional.
Fazendo primeiramente para a massa :
Simplificando:
Já para a outra massa:
Já para o período orbital, podemos usar a relação normal dele com a velocidade orbital:
Então:
Entrando com para a raiz, e substituindo o valor dele:
Simplificando:
Se fizermos o mesmo processo para a outra massa, encontraremos:
O que já era esperado, pois como o centro de massa não vai mudar a sua posição relativa entre as duas massas, o tempo que elas demoram para dar uma volta completa deve ser igual.
Muito conceito? Não esquenta! Dê uma exercitada que tudo vai ficar de boa! =)