12.12. As massas pontuais m e 2m estão situadas ao longo do eixo x, com m na origem e 2m em . Uma terceira massa pontual M é deslocada ao longo do eixo x. (a) Em que ponto a força gravitacional resultante sobre M em virtude das duas outras massas é igual a zero? (b) Desenhe o componente x da força resultante sobre M em virtude de m e 2m, supondo que as grandezas à direita sejam positivas. Inclua as regiões , e . Não deixe de mostrar o comportamento do gráfico em ambos os lados de e .
Passo 1
Vamos começar desenhando a situação.
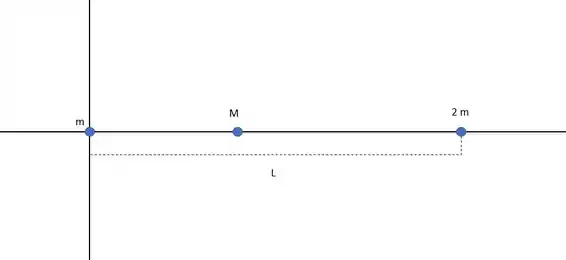
E a gente tem que descobrir onde a massa deve ficar de modo que a força gravitacional resultante seja 0.
Vamos lembrar de como se calcular a força de atração gravitacional
Onde e são as massas, é a distância entre os centros de gravidade dos corpos e é a constante gravitacional universal
Passo 2
Bem, a gente pode perceber que a terceira massa tem que estar entre as duas outras massas, porque a soma vetorial tem que ser 0, logo, as forças tem que estar em sentidos opostos, se ela não estiver entre as duas massas as forças gravitacionais vão se somar.
Sabendo disso, a gente pode dizer que a força gravitacional gerada pela interação com a massa de tem que ser igual a força gerada pela interação da massa de , logo
Olha só o tanto de coisa que a gente pode cortar, e
Se a gente inverter
Ou ainda
Logo
Isso quer dizer que a distância da massa de tem que ser maior que a distância de . Como a distância máxima que podemos ter é de então a gente pode fazer o seguinte
Mas
Logo
Então
Logo
E por tanto
Passo 3
Agora a gente tem que resolver o item (b). Para isso a gente precisa ver o comportamento das forças em cada ponto de x.
A gente pode fazer uma função que relaciona a posição x com a força que a massa exerce, as equações são bastante parecidas
Isso dá uma coisa desse tipo
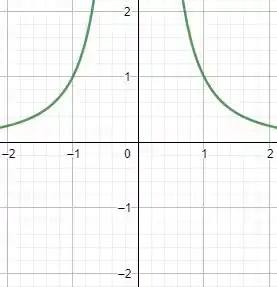
Sendo y a força e x a posição.
Isso nos dá algo assim
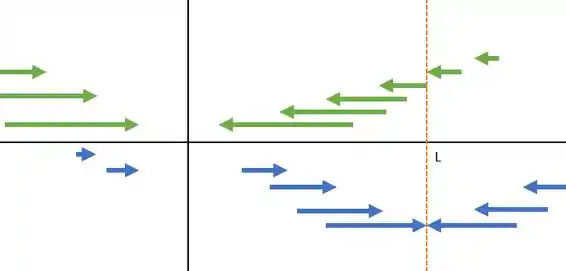
Os vetores verdes são gerados pela interação com a massa m e os vetores em azul são gerados pela interação com a massa de 2m.