Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 22.Problemas - Ex. 63
Uma carga positiva está distribuída uniformemente ao longo de cada volume de duas esferas de raio . Uma das esferas está centralizada na origem e a outra está centralizada no ponto (Figura ). Determine o módulo,a direção e o sentido do campo elétrico produzido por essas duas distribuições de cargas nos seguintes pontos sobre o eixo : ; ; ; .
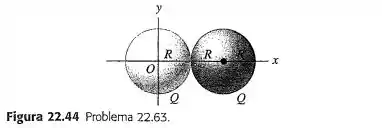
Passo 1
Para nós começarmos esse exercício, precisamos lembrar que o campo elétrico no interior de uma esfera isolante, com raio e carga distribuída uniformemente no seu volume, é dado por
E o campo elétrico na parte externa dessa mesma esfera é dado por:
Onde é a distância entre o centro da esfera até um determinado ponto, podemos usar essa equação e calcular o resultado para cada ponto dado, verificando se o ponto se encontra dentro ou fora de cada esfera.
Nesse caso, como ambas as esferas possuem cargas positivas distribuídas em seus volumes, seus campos elétricos irão apontar para fora dos seus respectivos centros.
Além disso, vamos representar os campos elétricos das esferas de acordo com suas posições no eixo , ou seja, e , tal que o campo resultante é a soma delas.
Passo 2
Dessa forma, para , o campo elétrico da esfera centralizada na origem será:
Pelo fato da distância entre o ponto em questão e o seu centro ser nulo.
Já para a outra esfera:
E tem sentido para a esquerda (lembrando que o seu campo flui para fora do seu centro).
Portanto, o campo elétrico resultante é:
No sentido negativo do eixo , ou ainda:
Passo 3
Analogamente, para , o campo elétrico da esfera centralizada na origem será:
Com sentido para a direita.
Já para a outra esfera:
Direcionado para a esquerda.
Portanto, o campo elétrico resultante é:
No sentido positivo do eixo , ou ainda:
Passo 4
Agora, para , o campo elétrico de ambas as esferas será dado por:
Pelo fato da distância entre o ponto e os seus centros serem iguais.
No entanto, como o ponto se encontra entre as esferas e seus campos apontam ambos para fora de seus centros, então somando-se esses campos elétricos:
Portanto:
O que se confirma, pois os campos têm a mesma intensidade e sentidos contrários.
Passo 5
Por fim, para , o campo elétrico da esfera centralizada na origem será:
No sentido .
Já para a outra esfera:
Também no sentido .
Portanto, o campo elétrico resultante é:
No sentido positivo do eixo , ou ainda: