Considere duas finas cascas cilíndricas, infinitamente longas e coaxiais. A casca interna tem raio e uma densidade superficial uniforme de cargas , e a casca externa tem raio e densidade superficial uniforme . (a) Use a lei de Gauss para determinar expressões para o campo ele´trico nas três regiões: , e , onde é a distância ao eixo. (b) Qual é a razão entre as densidades superficiais de carga e os sinais relativos se o campo elétrico foi igual a zero em toda a região exterior ao cilindro maior? (c) Para o caso da parte (b), qual seria o campo elétrico entre as cascas? (d) Esboce as linhas de campo elétrico para a situação da parte (b) se por positiva.
Passo 1
Eai gente. Nesse problema temos um problema de simetria cilíndrica. Vamos aproveitá-la para usar a lei de Gauss.
Passo 2
- Para , temos
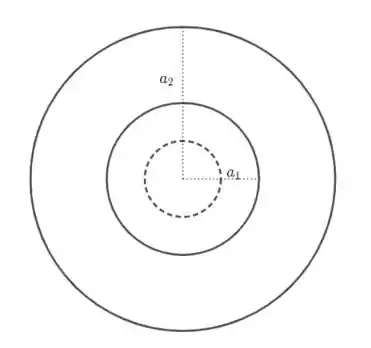
Claramente, temos . Assim, pela lei de Gauss, temos .
Passo 3
- Para , temos
- Para , temos
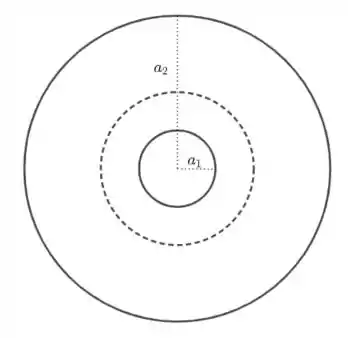
A carga interna será
Logo, pela lei de Gauss, temos
Passo 4
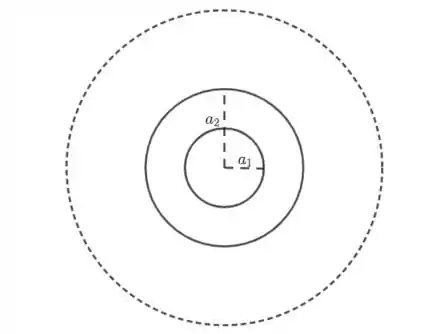
A carga interna será
Logo, pela lei de Gauss, temos que
Passo 4
note que os sinais devem ser contrários (como é esperado!)
Passo 5
Passo 6
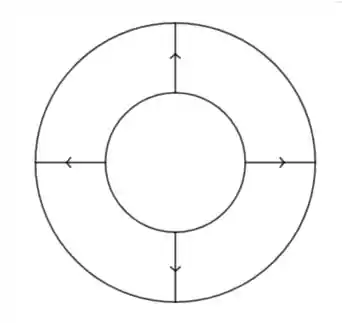
Note que apenas o campo entre os cilindros não é nulo.
Resposta
Ei, a resposta está no passo a passo :)