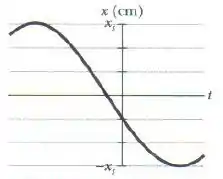
Qual é a constante de fase do oscilador harmônico cuja função posição x ( t ) aparece na figura se a função posição é da forma x = x m c o s ⁡ ( ω t + φ ) ? A escala do eixo vertical é definida por x s = 6,0c m .

A constante de fase do oscilador é φ = cos - 1 ⁡ ( 1 / 3 ) .

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.1 - Ex. 8

Qual é a constante de fase do oscilador harmônico cuja função posição aparece na figura se a função posição é da forma ? A escala do eixo vertical é definida por .

Passo 1

Show de bolinhas galerinha bonita, o grande desafio aqui é entender bem essa função da posição, expressa como:

A constante de fase é esse aí.

A primeira informação que a gente pode tirar do gráfico é olhando o ponto em que ele cruza o eixo .

Já que o enunciado diz que o , cada uma das três linhas horizontais ali “vale” , então o gráfico cruza o eixo nas coordenadas:

Substituindo isso na função, obtemos que:

Logo:

Agora falta achar o valor de .

Passo 2

Belezoca, o é simplesmente o deslocamento máximo do oscilador. Aquele gráfico do enunciado representa o deslocamento em função do tempo. Qual o valor máximo que ele atinge?

Exatamente meu patrão, é o próprio , ou seja:

Tal que:

E a resposta vai ser:

Mas se a gente jogar isso numa calculadore, obtemos os valores para dados como

Mas podemos excluir , pois esse ângulo leva a uma inclinação positiva da curva em , mas através do gráfico, podemos ver que a inclinação em é negativa!

Resposta

A constante de fase do oscilador é .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o movimento resultante de dois movimentos harmônicos simples na mesma direção dados por: x 1 = cos ⁡ ω t - π 6 , x 2 = sen ⁡ ω t . Represente graficamente os respectivos vetores girantes.

Trace as figuras de Lissajous corerespondentes à composição dos seguintes movimentos harmônicos simples em direções perpendiculares:(a) x = A cos ⁡ ω t , y = A sen ⁡ 2 ω t .(b) x = A sen ⁡ ω t , y = A

A FIGURA P14.32 é o gráfico velocidade versus tempo de uma partícula em movimento harmônico simples. a. Qual é a amplitude da oscilação? b. Qual é a constante de fase? c. Qual é a posição para t =0s ?

A FIGURA P14.31 é o gráfico posição versus tempo de uma partícula em movimento harmônico simples. a. Qual é a constante de fase? b. Qual é a velocidade em t =0s ? c. Quanto vale v m á x á ?

Um objeto em movimento harmônico simples tem amplitude de 8,0 cm e frequência de 0,50 Hz. Em t = 0s , ele tem sua velocidade mais negativa. Escreva a função x(t) que descreve a posição do objeto.