A esfera , com uma massa de , está situada na origem de um sistema de coordenadas ; a esfera , com uma massa de , está situada nas coordenadas ; a esfera , com uma massa de , está situada no primeiro quadrante, a de e de . Em termos dos vetores unitários, qual é a força gravitacional total que e exercem sobre .
Passo 1
Vamos começar desenhando as esferas e , mas deixando a de lado já que sua posição ainda não foi definida:
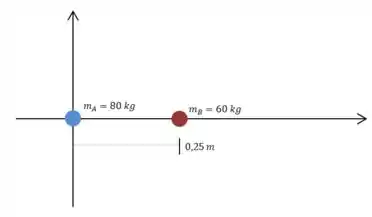
A questão pede para calcularmos a força (em termos de vetores unitários) que as esferas e exercem sobre .
Pela fórmula da força gravitacional, podemos achar facilmente os módulos dessas forças:
Passo 2
Substituindo os valores, temos:
Passo 3
Para acharmos as respostas em termos de vetores unitários, precisamos descobrir os ângulos que os vetores das forças formam com o eixo .
Quando acharmos, podemos substituir na fórmula (desde que ajustemos os sinais):
Vamos usar a lei dos cossenos para descobrir isso. Não dá pra desenhar exatamente, porque não sabemos a posição da esfera , mas imagine algo parecido com isso:
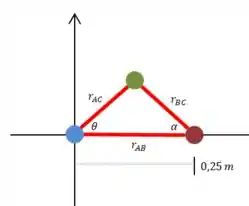
Pela lei dos cossenos temos:
Usando uma calculadora:
Além disso:
Passo 4
Agora vamos substituir esses resultados na fórmula mencionada antes:
Ajustando os sinais de acordo com o sentido dos vetores (lembrando que a gravidade é uma força atrativa):
Pronto!
Resposta
A força é