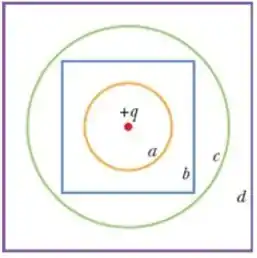
A Fig. mostra, em seção reta, duas esferas gaussianas e dois cubos gaussianos, no centro dos quais existe uma partícula de carga positiva. (a) Coloque as quatro superfícies gaussianas em ordem decrescente do fluxo elétrico que as atravessa. (b) Coloque as quatro superfícies gaussianas em ordem decrescente do módulo do campo elétrico em qualquer ponto da superfície, e informe se os módulos são uniformes ou variam de ponto para ponto da superfície.
![]()
Passo 1
Bora lá galera, Tudo bom ? Vamos juntos resolver mais um exercício !
É um exercício teórico então vamos estar afiados, Beleza!
Para as superfícies esféricas e cúbicas dadas, a carga encerrada é . Desde que todos os outros termos sejam constantes, o fluxo líquido através de todas as superfícies dadas é constante e, portanto, podemos usar a equação:
Portanto, a classificação do fluxo elétrico líquido através de todas as superfícies é:
Passo 2
Para as superfícies esféricas e cúbicas dadas, a carga encerrada é:
Assim, o campo elétrico com valor de carga constante depende da área da superfície gaussiana, ou seja, o fluxo do campo elétrico tem uma relação com a área da seguinte maneira:
E também temos que o campo elétrico depende da distância até a carga:
Agora, vamos classificar as áreas. Repare que a distância entre o centro (onde está localizada a carga ) e a superfície que queremos analisar, aumenta gradualmente. Desa forma, teremos:
Podemos diretamente, a partir dessa relação, perceber que, como o módulo do campo elétrico depende necessariamente da distância até a carga, ele terá valor mais intenso nas superfícies que estão mais próxima dela! Com isso, temos:
Agora repare, as superfícies esféricas (pelo próprio formato) possui uma distância constante do centro até sua superfície. Ou seja, o raio é constante. Para as superfícies cúbicas, a distância aumenta nas arestas, dessa forma, o campo elétrico possui um valor menor nessas regiões. Com isso, para as esferas, o campo elétrico é constante por toda superfície, enquanto que para as superfícies cúbicas, o campo elétrico será variável!
Então, concluímos o seguinte: