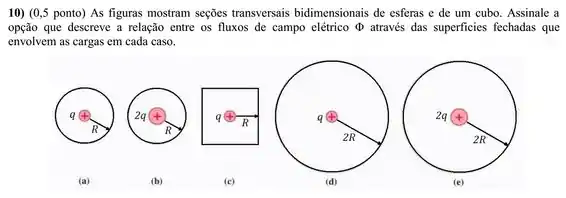
Exercícios de Introdução à Lei de Gauss - Lista de Exercícios Resolvida
Questão 1
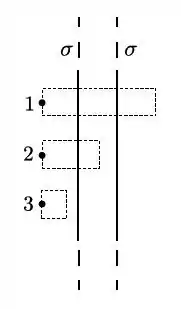
A figura representa o perfil de uma placa condutora de espessura finita e demais dimensões muito maiores que . A densidade superficial de carga em ambas as faces da placa é constante (uniforme e estacionária). Considerando as três superfícies cilíndricas indicadas na figura, qual das afirmativas abaixo é correta?
Questão 2
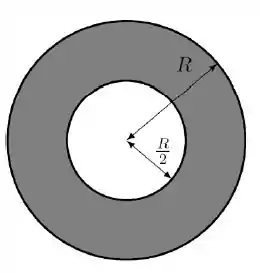
Numa esfera dielétrica oca existe uma densidade volumétrica de cargas constante. O raio externo da esfera é igual a e o raio do buraco esférico concêntrico é igual a , conforme a figura. Determine o fluxo elétrico através de uma gaussiana esférica concêntrica de raio .
Questão 3
Determine o campo elétrico gerado por uma esfera sólida uniformemente carregada que tem raio e uma carga total , distribuída uniformemente através do volume da esfera cuja densidade de carga é onde é o volume da esfera.
Ver solução completaQuestão 4
Uma carga puntiforme de está colocada no centro de uma superfície Gaussiana cúbida, de aresta igual a . Qual o valor de para essa superfície:
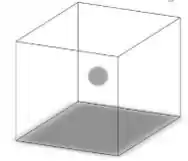
Questão 5
Um elétron se encontra no centro de um cubo cuja aresta mede . Calcule o fluxo elétrico através de uma das faces do cubo.
Ver solução completaQuestão 6
Considere os seguintes sistemas carregados:
- Fio retilíneo, fino, finito, uniforme;
- Fio retilíneo, fino, finito, não uniforme;
- Fio retilíneo, fino, infinito, não uniforme;
- Anel circular, fino, uniforme;
- Bola (esférica), sólida, com densidade de carga variando só com a distância até o centro.
Qual a opção que indica, desses sistemas, aquele(s) para o(s) qual(is) pode-se aplicar a lei de Gauss a fim de deduzir uma expressão analítica explícita para o campo elétrico resultante?
- IV
- V
- I, IV
- I, V
- IV, V
- I, IV, V
Questão 7
Determine o campo elétrico devido a uma fina casca esférica carregada de raio e carga total .
Ver solução completaQuestão 8
Seja um cubo isolante e uniformemente carregado, isolado de todos os outros corpos.
Dentre as afirmações
A lei de Gauss só se aplica a esse problema se escolhermos superfícies gaussianas cúbicas, haja vista a simetria do sistema,
A lei de Gauss deixa de ser aplicável a esse problema se escolhermos superfícies gaussianas que interceptam o cubo carregado,
A lei de Gauss simplesmente não se aplica a esse problema;
qual(is) é(são) verdadeira(s)?
Somente a .
Somente a .
Somente a .
Somente a e a .
Somente a e a .
Somente a e a .
Todas estão corretas.
Nenhuma está correta.
Ver solução completaQuestão 9
Uma superfície imaginária esférica fechada envolve completamente um dipolo elétrico e nenhuma outra partícula carregada. Podemos afirmar que:
o campo elétrico é zero em todos os pontos da superfície.
o campo elétrico possui módulo constante em todos os pontos da superfície.
o campo elétrico é normal à superfície em todos os seus pontos.
o fluxo do campo elétrico através de uma parte da superfície pode não ser igual a zero.
o fluxo do campo elétrico através da superfície não pode ser igual a zero, pois há cargas envolvidas pela mesma.
Ver solução completaQuestão 10
Um cilindro circular infinito e isolante, de raio , possui uma distribuição volumétrica de carga uniforme. Que tipo de dependência com a distância ao eixo do cilindro podemos esperar para a intensidade do campo elétrico, , na região do espaço definida por ?
Questão 12
O desenho abaixo ilustra uma casca esférica condutora neutra com uma carga em seu interior.
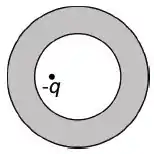
A carga está posicionada fora do centro de simetria da casca esférica e o sistema se encontra em equilíbrio. Marque a opção que melhor ilustra o diagrama de linhas de campo deste sistema.
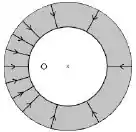
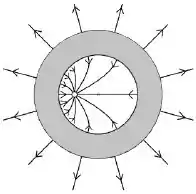
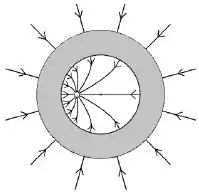
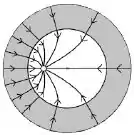
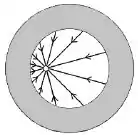
Questão 13
Uma carga está uniformemente distribuída sobre a superfície de uma casca condutora. Uma partícula puntiforme com carga está no interior da casca. A força elétrica sobre a partícula tem a maior intensidade quando:
a) ela está próxima à superfície interna da casca.
b) ela está no centro da casca.
c) ela está no meio do caminho entre o centro da casca e a superfície da casca.
d) ela está em qualquer ponto interior (a força é a mesma em qualquer ponto nessa região e não é zero).
e) ela está em qualquer ponto interior (a força é zero em qualquer ponto nessa região).
Ver solução completaQuestão 14
Analise as seguintes afirmativas:
Em uma certa região do espaço, a carga elétrica total é zero; logo, em qualquer ponto de sua superfície fronteiriça, o campo elétrico também é zero;
Em equilíbrio eletrostático, o campo elétrico no interior de um material isolante, é, necessariamente, zero;
Se um condutor, em equilíbrio eletrostático, é neutro, então a densidade superficial de carga em qualquer ponto de sua superfície é nula.
Qual(is) é(são) verdadeira(s)?
Apenas a .
Apenas a .
Apenas a .
Apenas a e a .
Apenas a e a .
Apenas a e a .
Todas são verdadeiras
Nenhuma é verdadeira.
Ver solução completaQuestão 15
A figura abaixo mostra uma superfície cúbica com uma carga elétrica localizada em seu centro.
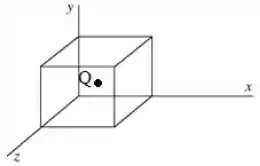
O fluxo do campo elétrico através da face superior dessa superfície cúbica vale:
Ver solução completa
Questão 16
O campo elétrico produzido por duas cascas cilíndricas co-axiais longas é representado pelas linhas de campo elétrico indicadas abaixo. A carga na casca cilíndrica interna é .
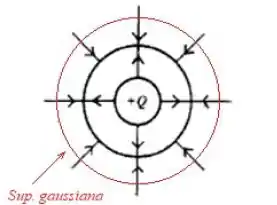
Das respostas abaixo a única opção que pode representar a carga na casca cilíndrica externa é:
zero
Ver solução completaQuestão 17
Considere um cubo uniformemente carregado com densidade volumar . Um aluno deseja calcular o campo elétrico em um ponto fora do cubo e para isso resolve usar a lei de Gauss traçando uma superfície gaussiana cúbica que passa pelo ponto . Ele faz as seguintes afirmações sobre o problema:
A lei de Gauss vale nessa situação;
Para usar a lei de Gauss, basta escolher uma superfície gaussiana que tenha a mesma simetria do objeto em questão;
Tendo o objeto e a superfície gaussiana simetria cúbica, é possível afirmar que o campo é constante sobre a superfície gaussiana.
Qual(is) delas é(são) verdadeira(s)?
Nenhuma.
Somente a .
Somente a .
Somente a .
Somente a e a .
Somente a e a .
Somente a e a .
Todas.
Ver solução completaQuestão 18
Uma partícula pontual de carga está na presença de uma esfera condutora aterrada. Verifica-se que o fluxo do campo elétrico através de uma superfície gaussiana que engloba a partícula e a esfera é , com . São feitas então as seguintes afirmativas.
- Caso a superfície gaussiana envolvesse apenas a esfera condutora, o fluxo seria
- A carga total induzida na esfera condutora é negativa.
- A esfera condutora possui uma distribuição de cargas em sua superfície. Porém sua carga total é nula.
- A carga total contida dentro da superfície gaussiana é positiva.
São verdadeiras:
- I e II
- I, II e IV
- I, III e IV
- III e IV
- I e IV
Questão 19
Seja um cubo isolante e uniformemente carregado, isolado de todos os outros corpos.
Dentre as afirmações
A lei de Gauss só se aplica a esse problema se escolhermos superfícies gaussianas cúbicas, haja vista a simetria do sistema,
A lei de Gauss deixa de ser aplicável a esse problema se escolhermos superfícies gaussianas que interceptam o cubo carregado,
A lei de Gauss simplesmente não se aplica a esse problema;
qual(is) é(são) verdadeira(s)?
Somente a .
Somente a .
Somente a .
Somente a e a .
Somente a e a .
Somente a e a .
Todas estão corretas.
Nenhuma está correta.
Ver solução completaQuestão 20
Uma esfera isolante de raio possui uma densidade volumétrica de carga dada por , onde é uma constante a ser determinada e é a distância ao centro da esfera. Sabendo que a carga total da esfera vale , podemos afirmar que o valor de e o vetor campo elétrico produzido por ela a uma distância são, respectivamente:
Escolha uma:
Questão 21
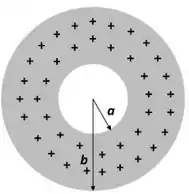
Uma esfera sólida isolante carregada de raio R é envolvida por uma casca esférica condutora de raio interno e raio externo e carga líquida nula. As cargas da esfera isolante estão distribuídas de forma esfericamente simétrica com densidade volumétrica de cargas , onde r é à distância com relação ao centro da esfera.
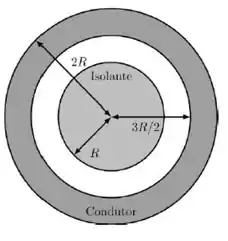
a) Se considerarmos que , qual deve ser o valor de α para que o campo elétrico a uma distância do centro da configuração seja nulo? Em outras palavras, E(4R/3) = 0.
Para os próximos itens considere que . Utilizando a Lei de Gauss, encontre a magnitude do campo elétrico E(r) nas regiões:
b) r
c) R
d)3R/2
e)2R
Considere, apenas para o item (f), que e.
f) Calcule a densidade superficial de carga σ da superfície externa da casca condutora.
Ver solução completaQuestão 22
Considere as seguintes afirmativas:
Partículas carregadas, no exterior de uma superfície fechada , não contribuem nem para o fluxo do campo elétrico através de , nem para o campo elétrico resultante em pontos de ;
Se o fluxo do campo elétrico através de uma superfície fechada for zero, não há partículas carregadas no interior de tal superfície;
A lei de Gauss só vale para distribuições de carga simétricas.
Qual(is) delas é(são) verdadeira(s)?
Nenhuma.
Somente a .
Somente a .
Somente a .
Somente a e a .
Somente a e a .
Somente a e a .
Todas.
Ver solução completaQuestão 23
Uma carga está dentro de uma pirâmide como mostrado na figura abaixo. A pirâmide tem o comprimento de um dos lados da base igual a unidades e altura unidades.
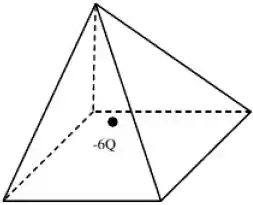
Qual é o fluxo elétrico total através da pirâmide?
Ver solução completa
Questão 24
Quatro dipolos, cada um consistindo de uma carga e outra carga de , estão localizados no plano com seus centros distando da origem. Uma superfície esférica passa através dos dipolos, como indicado na figura.
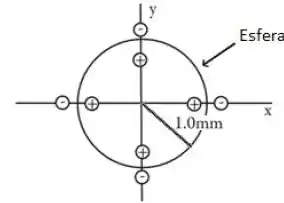
O fluxo elétrico através desta superfície vale:
Ver solução completa
Questão 25
Uma carga é distribuída uniformemente sobre uma casca esférica isolante. Uma carga pontual é colocada dentro da casca. Qual alternativa melhor descreve a força elétrica sobre a partícula com carga :
- A força é maior quando está próximo da superfície interna da casca.
- A força é maior quando está no centro da casca.
- A força é maior quando está a meio caminho entre o centro e a superfície interna da casca.
- A força é nula em qualquer posição dentro da casca.
- A força é constante e diferente de zero em qualquer posição dentro da casca.
Questão 26
Considere uma superfície gaussiana esférica de raio centrada na origem. Uma carga é colocada dentro da esfera. Para maximizar a magnitude do fluxo do campo elétrico através da superfície gaussiana, a carga deve estar localizada
(a) em qualquer lugar, uma vez que o fluxo não depende da posição da carga, desde que esteja dentro da esfera;
(b) na origem;
(d) em ;
(e) em ;
(c) em ;
Ver solução completaQuestão 27
Seja uma região delimitada por uma superfície fechada . Tal região possui uma densidade volumar de carga e uma carga total . A partir da lei de Gauss, pode-se dizer que:
Se , o campo elétrico é nulo no interior de .
Se , o campo elétrico é nulo no interior de .
Se , o campo elétrico é nulo em .
Se , o campo elétrico é nulo em .
Nenhuma das opções anteriores.
Ver solução completaQuestão 28
Uma casca esférica condutora está eletrizada com carga , no vácuo. A Lei de Gauss nos mostra que, para pontos do espaço exteriores à casca, podemos considerar toda carga concentrada em seu centro.
Verdadeiro ou falso?
Ver solução completaQuestão 29
Uma partícula com carga é colocada no interior de um cubo, mas não no centro dele. O fluxo elétrico através de qualquer face do cubo é:
;
;
;
zero;
não pode ser calculado usando a lei de Gauss;
Ver solução completaQuestão 30
Uma esfera dielétrica sólida com raio tem carga uniformemente distribuída em seu volume. Uma casca esférica condutora fina, eletrizada com carga envolve a esfera. (Considere as distâncias medidas com referência ao centro da esfera sólida). Nessas condições, quanto vale , a soma das intensidades dos campos gerados à distância e à distância ? Se necessário use .
Ver solução completa