Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 35.4 - Ex. 40
Um filme fino de acetona () está sobre uma placa espessa de vidro (). Um feixe de luz branca incide perpendicularmente ao filme. Nas reflexões, a interferência destrutiva acontece para e a interferência construtiva para . Determine a espessura do filme de acetona.
Passo 1
A questão trata sobre interferência em filmes finos. A figura ilustra a situação com um filme fino de sabão entre duas camadas de ar.
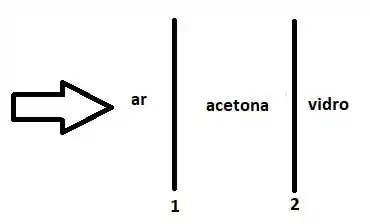
Tanto na reflexão na interface 1 comona interface 2 vai ocorrer inversão de fase na onda, de modo que não precisamos considerar isso para defasagem:
Como
Temos que
Passo 2
Para interferência destrutiva, temos
Assim, para que a interferência seja destrutiva, temos que :
Já para que a interferência seja construtiva com :
Passo 3
Igulando as expressões:
Temos que achar os menores e inteiros que satisfazem essa expressão! Note que e resolve nosso problema:
Nos dois casos: