Exercícios de Interferência em Filmes Finos - Lista de Exercícios Resolvida
Questão 1
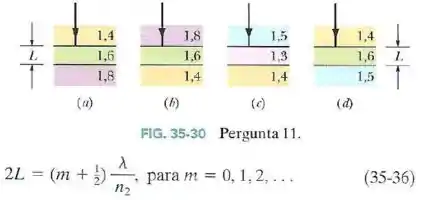
A Fig.35-30 mostra quatro situações nas quais a luz incide perpendicularmente em um filme fino de largura situado entre placas muito mais espessas feitas de materiais diferentes. Os índices de refração são dados.
Em que situações a Eq.35-36 corresponde à condição para que a intensidade da onda refletida seja máxima (ou seja, para que o filme pareça claro)?
Questão 2
Uma película de sabão ) com de espessura é iluminada perpendicularmente com luz branca. Para quantos comprimentos de onda diferentes na faixa de a a luz refletida apresenta (a) interferência construtiva total e (b) interferência destrutiva total?
Ver solução completaQuestão 3
A reflexão de um feixe de luz branca que incide perpendicularmente em uma película uniforme de sabão suspensa no ar apresenta um máximo de interferência em , e o mínimo mais próximo está em .
Se o índice de refração da película é , qual é a sua espessura?
Ver solução completaQuestão 4
Um feixe de luz branca incide perpendicularmente, de cima para baixo, em um filme fino horizontal colocado entre placas espessas de dois materiais. Os índices de refração são para o material de cima, para o filme fino e para o material de baixo.
A espessura do filme é . Dos comprimentos de onda da luz visível ( a ) que resultam em interferência construtiva total para um observador situado acima do filme, qual é:
- O maior comprimento de onda?
- O menor comprimento de onda?
- Os materiais e o filme são aquecidos, o que faz a espessura do filme aumentar. A interferência construtiva total passa a ocorrer para um comprimento de onda maior ou menor?
Questão 5
A lente de uma câmara, com índice de refração maior que , é revestida com um filme fino transparente com um índice de refração de para eliminar por interferência a reflexão de luz com comprimento de onda que incide perpendicularmente na lente.
Que múltiplo de corresponde à espessura mínima de um filme que atende a essas especificações?
Ver solução completaQuestão 6
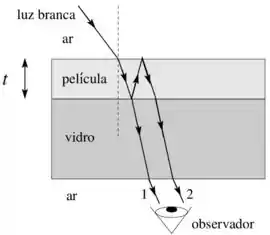
Um raio de luz monocromática incide perpendicularmente em um filme fino de água de espessura , sobre um bloco de vidro de espessura como mostrado na figura abaixo.
Dois observadores, e , determinam o critério para que a diferença de fase total dos raios emergentes leve a uma interferência destrutiva.
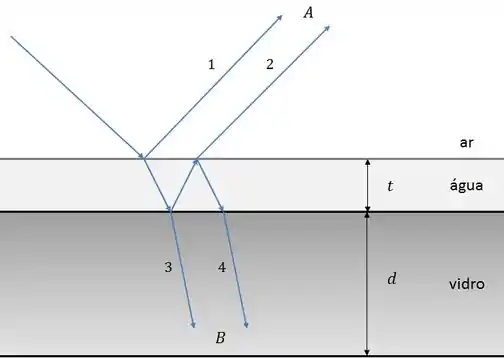
De acordo com os observadores e, respectivamente, a interferência será destrutiva quando:
- ;
- ;
- ;
- ;
- ;
- Nenhuma das anteriores
Questão 7
Uma placa de vidro com um índice de refração de deve ser revestida com um filme fino de um material com um índice de refração de para que uma luz verde com um comprimento de onda no ar de seja transmitida preferencialmente através de uma interferência construtiva.
- Qual é a espessura mínima do filme para que esse objetivo seja conseguido?
- Por que outras partes do espectro visível também não são transmitidas preferencialmente?
- A transmissão de alguma(s) cor(es) é reduzida significativamente? Qual ou quais?
Questão 8
Os diamantes de imitação usados em bijuteria são feitos de vidro com índice de refração . Para que reflitam melhor a luz, costuma-se revesti-los com uma camada de monóxido de silício de índice de refração .
Determine a menor espessura da camada de monóxido de silício para que uma onda de comprimento de onda e incidência perpendicular sofra interferência construtiva ao ser refletida pelas duas superfícies da camada.
Ver solução completaQuestão 9
Um filme fino de um certo líquido é mantido em um disco horizontal, com ar dos dois lados do filme. Um feixe de luz com um comprimento de onda de incide perpendicularmente ao filme, e a intensidade da reflexão é medida.
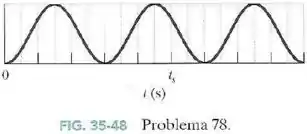
A Fig.35-48 mostra a intensidade em função do tempo ; a escala do eixo horizontal é definida por . A intensidade muda por causa da evaporação nas duas superfícies do filme.
Suponha que o filme é plano, que as duas superfícies do filme são paralelas e que o filme tem um raio de e um índice de refração de . Suponha também que o volume do filme diminui a uma taxa constante.
Determine essa taxa.
Questão 10
Um filme fino () é depositado em uma placa de vidro () e iluminado com uma luz cujo comprimento de onda no ar é . A luz incide perpendicularmente na placa.
Qual é a espessura mínima (diferente de zero) para que o filme:
- Transmita o máximo de luz.
- Reflita o máximo de luz.
Questão 11
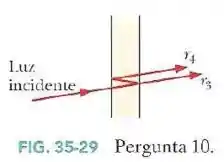
A Fig.35-29 mostra a passagem de um raio de luz perpendicular (mostrado com uma pequena inclinação para tornar a figura mais clara) por um filme fino suspenso no ar.
- O raio sofre uma mudança de fase por reflexão?
- Qual é a mudança de fase por reflexão fo raio , em comprimentos de onda?
- Se a espessura do filme é , qual é a diferença de percurso entre os raios e ?
Questão 12
Uma onda luminosa de comprimento de onda incide perpendicularmente em uma película de sabão (com ) suspensa no ar.
Quais são as duas menores espessuras do filme para as quais as ondas refletidas pelo filme sofrem interferência construtiva?
Ver solução completaQuestão 13
Um filme fino com um índice de refração de é introduzido em um dos braços de um interferômetro de Michelson. Isto causa um deslocamento de franjas claras da figura de interferência produzida por uma luz com um comprimento de onda de . Qual a espessura do filme?
Questão 14
Observa-se o fenômeno da interferência em uma lâmina delgada de espessura e índice de refração ao ser iluminada com luz branca em incidência quase perpendicular à superfície. A lâmina está imersa em água cujo índice de refração é menor que o da lâmina.
Determine a menor espessura da lâmina para que a luz de comprimento de onda (referido no vácuo) tenha uma reflexão intensa (máximo).
Ver solução completaQuestão 15
Seja um feixe de luz monocromática tal que seu campo elétrico representado por . Um estudante faz algumas observações com um polarizador e com amostras de um cristal.
a) Inicialmente sem o cristal, incidindo o feixe de luz diretamente no polarizador e analisando a luz emergente, ele mede a intensidade da luz quando o polarizador está alinhado ao eixo . Qual a intensidade observada, comparada com a incidente?
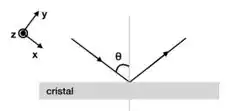
b) Incidindo o feixe sobre a superfície do cristal, para um ângulo de incidência de e então passando a luz refletida pelo polarizador, ele observa que a luz está polarizada no eixo . Qual é o índice de refração do cristal e com que ângulo a luz é refratada dentro do cristal?
c) Incidindo o feixe na direção normal à superfície de uma lâmina desse cristal, suspensa na atmosfera, o estudante observa que não há luz refletida pela superfície. Sabendo que o comprimento de onda da luz é e que a espessura da lâmina está no intervalo , encontre essa espessura.
(Para não do resultado do item anterior, tome ).
Ver solução completaQuestão 16
Uma película muito fina de material transparente, de índice de refração é utilizada como revestimento anti-refletor na superfície de um vidro de índice de refração de uma célula solar.
Qual deve ser a espessura mínima da película para numa incidência perpendicular não se observar por reflexão a luz que no vácuo tem comprimento de onda ?
Ver solução completaQuestão 17
(a) Em um experimento similar ao experimento de Young, uma das fendas é coberta com
uma fina placa de quartzo ( = 1,58) e a outra com uma fina camada de zircônio ( =
1,92), ambas de mesma espessura. Nessas condições, observa-se que, para incidência
de uma onda com λ = 650 nm, o ponto central da tela de observação passa a ser
ocupado pela terceira franja lateral clara (m=3) da figura de interferência original (sem
placas recobrindo as fendas). Justifique a razão para este deslocamento de franjas e
determine qual é a espessura das placas.
Ver solução completaQuestão 18
Um raio de luz monocromática incide quase perpendicularmente em um filme fino de água de espessura , sobre um bloco de vidro de espessura , como mostra a figura abaixo. Se os índices de refração dos meios satisfazem , pode-se concluir que a interferência em A será construtiva:
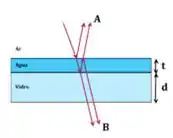
a) com , na qual é um número natural e , o comprimento de onda da luz na água.
b) com , na qual é um número natural e , o comprimento de onda da luz na água.
c) com , na qual é um número natural e , o comprimento de onda da luz no ar.
d) com , na qual é um número natural e , o comprimento de onda da luz no ar
Ver solução completaQuestão 19
– Observa-se o fenômeno da interferência em uma lâmina delgada de espessura ao ser iluminada com luz branca em incidência quase perpendicular à superfície.
A lâmina está flutuando na água com sua face superior no ar e face inferior dentro d’água. Os índices de refração são respectivamente , e .
Determine a menor espessura da lâmina () para que a luz de comprimento de onda 5 (referido ao vácuo) tenha uma reflexão intensa (máximo).
Ver solução completaQuestão 20
– Observa-se o fenômeno da interferência em uma lâmina delgada de espessura ao ser iluminada com luz branca em incidência quase perpendicular à superfície.
A lâmina está flutuando na água com sua face superior no ar e face inferior dentro d’água. Os índices de refração são respectivamente , e .
Determine a menor espessura da lâmina () para que a luz de comprimento de onda (referido ao vácuo) tenha uma reflexão intensa (máximo).
Ver solução completaQuestão 21
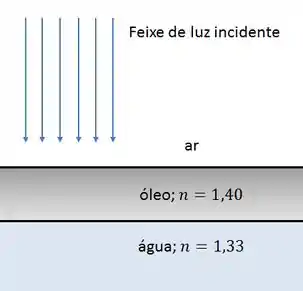
Um filme fino de azeite com flutua sobre uma bacia de água com .
Desprezando múltiplas reflexões internas, o feixe que retorna terá intensidade mínima no caso em que a espessura do filme, em nanômetros, seja:
Obs:
no ar.
Ver solução completaQuestão 22
Em experimento com anéis de Newton o raio de curvatura da lente é 𝑅 = 6,0 𝑚 e seu diâmetro vale 𝑑 = 10 𝑚𝑚. O comprimento de onda é 589 𝑛𝑚. Admita que haja anéis de Newton até a borda da lente,
(a) Determine o número de anéis claros formados.
Ver solução completaQuestão 23
Um raio de luz monocromática incide perpendicularmente em um filme fino de água de espessura , sobre um bloco de vidro de espessura , como mostrado na figura abaixo.
Dois observadores, e , determinam o critério para que a diferença de fase total leve a uma interferência construtiva, sabendo que . De acordo com os observadores e , respectivamente, a interferência será construtiva quando:
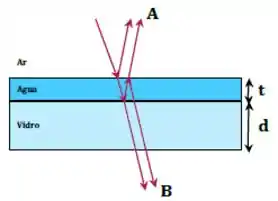
- e
- e
- e
- e
- e
- e
Questão 24
Uma película especial, com índice de refração , é projetada para aumentar a refletividade da radiação solar. A película é fixada na parte de fora de um vidro com índice de refração .
Qual deve ser a espessura mínima da película para diminuir a transmissão da radiação no infravermelho ()?
Questão 25
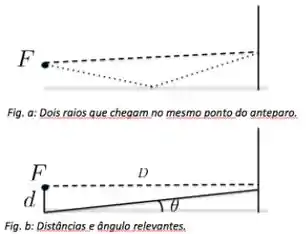
A figura abaixo ilustra o funcionamento de um espelho de Lloyd.
Luz emitida por uma fonte puntiforme pode atingir o anteparo diretamente ou então através de uma reflexão no espelho horizontal, provocando um padrão de interferência no anteparo. Dois destes raios (um pontilhado e outro tracejado) estão indicados na figura .
Seja a distância entre a fonte e o plano do espelho, a distância entre a fonte e o anteparo () e o ângulo de observação, conforme ilustrado na figura .
Sabendo que ao refletir no espelho a onda luminosa ganha uma fase de , assinale a alternativa que está INCORRETA.
- O padrão de interferência produzido é equivalente a termos duas fontes emitindo coerentemente e defasadas por , com a segunda fonte estando na posição da imagem da primeira, com relação ao espelho plano.
- O espaçamento entre os máximos e mínimos consecutivos na interferência é dado por .
- Uma região com interferência destrutiva no anteparo se dá em .
- A intensidade máxima no anteparo é quatro vezes maior do que a intensidade emitida pela fonte .
- A intensidade média ao longo de um período de oscilação é , onde é intensidade emitida por .
Questão 26
Um filme fino de espessura t variável e índice de refração n2 é iluminado por luz
monocromática de comprimento de onda que no vácuo é igual a . O filme encontra-se
imerso em um meio cujo índice de refração . Observa-se a interferência
dos raios 1 e 2 provenientes da reflexão da luz nas superfícies superior e inferior do
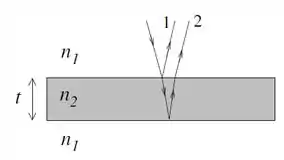
filme, conforme a figura. Considere incidência normal.
a)Calcule o valor a mínimo da espessura do filme para que a intensidade
da luz observada seja máxima.
b)Calcule o valor b mínimo da espessura do filme para que a intensidade da luz observada seja mínima.
Ver solução completaQuestão 27
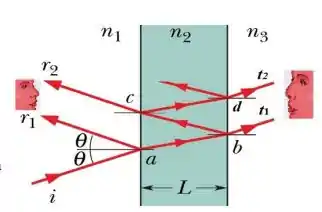
A figura ao lado mostra uma onda incidente quase normal à superfície de um filme fino (índice de refração ) suspenso no ar ( = = ) onde > . A onda é a refletida na primeira superfície em a. A onda é a refletida em b (dentro do filme) e transmitida de volta para o ar na primeira superfície em c. As ondas transmitidas que atravessam o filme são dadas por e . Considere L a espessura do filme e λ o comprimento de onda da luz no filme. Os observadores estão representados pelos rostos desenhados. Ocorre interferência construtiva:
1-( ) se L = para observador que vê as ondas e .
2-( ) se L = para observador que vê as ondas e .
3-( ) se L = para observador que vê os ondas transmitidas e .
4-( ) se L = para observador que vê os ondas transmitidas e .
Ver solução completaQuestão 28
Um feixe de luz branca incide perpendicularmente, de cima para baixo, em um filme fino colocado entre placas horizontais espessas de dois materiais. Os índices de refração são para o material de cima, para o filme fino e para o material de baixo. A espessura do filme é . A luz refletida é então analisada.
(b) Quais são o maior e o menor comprimentos de onda que resultam em interferência construtiva para um observador situado acima do filme?
Ver solução completaQuestão 29
Um feixe de luz branca incide perpendicularmente, de cima para baixo, em um filme fino colocado entre placas horizontais espessas de dois materiais. Os índices de refração são para o material de cima, para o filme fino e para o material de baixo. A espessura do filme é . A luz refletida é então analisada.
- Discuta se ocorre diferença de fase devido à reflexão analisando o que acontece em cada interface (– e –).
Questão 30
Em experimento com anéis de Newton verificou-se a presença de um ponto escuro no centro da imagem. Diga se é Falso ou Verdadeiro e justifique.
Ver solução completaQuestão 31
Um feixe de luz de comprimento de onda incide perpendicularmente sobre um filme fino de de espessura e índice de refração igual a .
Parte da luz penetra no filme e é refletida na face interna inferior do filme.
- Calcule o número de comprimentos de onda contidos ao longo da trajetória da luz dentro do filme, desde o ponto de incidência até o ponto de saída da luz na face superior.
- Calcule a diferença de fase entre a onda refletida na face superior e a onda emergente proveniente da reflexão na face interna inferior.
Questão 32
Um filme de poliuretano com índice de refração é colocado sobre a superfície plana de um material com índice de refração .
Qual a espessura mínima do filme de poliuretano para que a luz de comprimento de onda de seja predominantemente refletida?
Caso a indústria te informe que não tem maquinário para produzir um filme tão fino, qual seria a próxima espessura que satisfaria o teu propósito?
e
e
e
e
e
e
e
Nenhuma das anteriores
Ver solução completaQuestão 33
Considere um feixe de luz monocromática com comprimento de onda que se propaga no ar e incide quase perpendicularmente numa camada de vidro com índice de refração , muito fina, de espessura igual a .
Podemos afirmar que o feixe refletido, em relação ao feixe incidente, terá uma intensidade:
igual a do feixe incidente
menor do que a do feixe incidente
maior do a do feixe incidente
com os dados fornecidos não é possível afirmar nada
nenhuma das respostas anteriores
Ver solução completaQuestão 34
Luz monocromática de comprimento de onda incide sobre uma fenda . Um espelho metálico plano está a uma distância abaixo de , muito menor do que a separação entre a fenda e a tela.
Na tela aparecem faixas claras e escuras devido à interferência entre as ondas que partem de e atingem a tela diretamente e via reflexão no espelho.
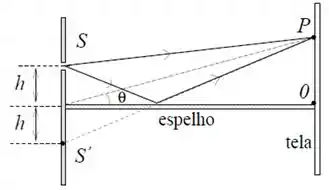
- Contrariamente à experiência de Young, a franja para no ponto da tela é escura. Explique a diferença.
- Deduza a condição que o ângulo deve satisfazer para haver interferência construtiva entre as ondas diretas e refletidas no ponto da tela. Observe que o raio refletido percorre a mesma distância que o raio que parte da imagem virtual da fenda no espelho (veja a figura).
Questão 35
Um derramamento de querosene de um navio cria uma mancha na superfície do mar. O índice de refração do querosene é e o da água .
Os comprimentos de onda da luz visível se encontram no intervalo entre e .
- Voando de avião sobre a mancha e olhando diretamente para baixo numa região em que a mancha tem espessura de quais são os comprimentos de onda da luz visível que interferem construtivamente?
- Para um mergulhador na mesma região mas embaixo da mancha qual é o comprimento de onda da luz visível que interfere construtivamente?
- Na região da mancha, onde a espessura é muito menor do que os comprimentos de onda de luz visível, o observador no avião vê uma interferência construtiva ou destrutiva? Justifique sua resposta.
Questão 36
Um raio de luz monocromática incide perpendicularmente em um filme fino de água de espessura , sobre um bloco de vidro de espessura como mostrado na figura abaixo.
Dois observadores, e , determinam o critério para que a diferença de fase total dos raios emergentes leve a uma interferência destrutiva.
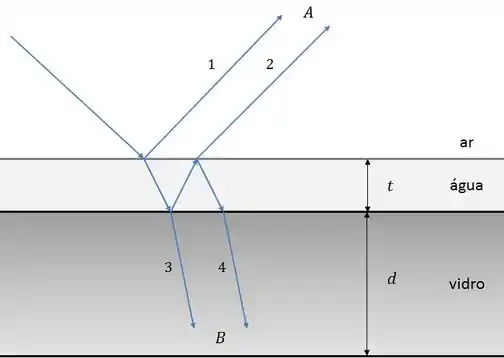
De acordo com os observadores e, respectivamente, a interferência será destrutiva quando:
- ;
- ;
- ;
- ;
- ;
- Nenhuma das anteriores
Questão 37
Uma onda eletromagnética de comprimento de onda λ = 600 nm .incide sobre um dispositivo de interferência tipo Young. Após as duas fendas saem duas ondas em fase que se superpõem em uma tela de observação distante produzindo interferência. Na saída de uma das fendas coloca-se uma placa de Mica com índice de refração n = 1,58 e espessura X. Em consequência ocorre um deslocamento do padrão de interferência por 7 máximos sucessivos para o lado onde foi colocada a placa de Mica. Determine a espessura X dessa placa de Mica.
Ver solução completaQuestão 38
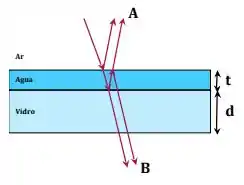
Um feixe de luz monocromático incide quase perpendicularmente em um filme fino de água de espessura t que está sobre um bloco de vidro de espessura d, como mostrado a figura. Dois observadores A e B determinam o respectivo critério para que a diferença de fase total dos raios emergentes leve a uma interferência CONSTRUTIVA. Considere a seguinte relação entre os índices de refração . De acordo com os observadores A e B, respectivamente, a interferência será CONSTRUTIVA quando (m e n são números inteiros positivos):
(a) e
(b) e
(c) e
(d) e
(e) e
(f) e
Ver solução completaQuestão 39
Um feixe de luz branca incide perpendicularmente, de cima para baixo, em um filme fino colocado entre placas horizontais espessas de dois materiais. Os índices de refração são para o material de cima, para o filme fino e para o material de baixo. A espessura do filme é . A luz refletida é então analisada.
(c) Se a espessura do filme é aumentada, a interferência construtiva passa a ocorrer para comprimentos de onda maior ou menor, comparado àqueles para a espessura anterior?
Ver solução completaQuestão 40
– Observa-se o fenômeno da interferência em uma lâmina delgada de espessura ao ser iluminada com luz branca em incidência quase perpendicular à superfície.
A lâmina está flutuando na água com sua face superior no ar e face inferior dentro d’água. Os índices de refração são respectivamente , e .
Determine a menor espessura da lâmina () para que a luz de comprimento de onda (referido ao vácuo) tenha uma reflexão intensa (máximo).
Ver solução completaQuestão 41
Um feixe de luz plana monocromática, viajando no ar, incide sobre uma placa de Zircônio, cujo índice de refração é .
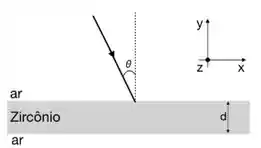
a) Seja o ângulo de incidência . Qual de propagação da luz dentro do Zircônio? Escreva em termos dos vetores unitários , e , de acordo com o sistema de coordenadas mostrado na figura).
b) Suponha que a espessura da placa de Zircônio seja . Se a luz parte de uma posição acima da face superior da placa, quanto tempo leva para emergir na face inferior da placa?
c) Seja agora (incidência normal) e a espessura da placa de Zircônio . Para quais comprimentos de onda dentro do espectro visível a intensidade da luz refletida (emergindo pela face superior da placa) é nula?
Ver solução completaQuestão 42
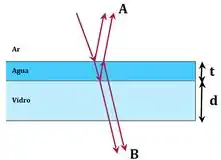
Um raio de luz monocromático com comprimento de onda , no ar, incide quase-perpendicularmente em um filme fino de água de espessura , sobre um bloco de vidro de espessura , como mostra a figura fora de escala abaixo. Sabendo que os índices de refração de cada meio valem, respectivamente, , e , determine um valor de para que a interferência em seja construtiva.
Questão 43
A figura abaixo mostra uma camada superior de índice de refração de espessura , depositada sobre uma camada espessa de índice de refração . O sistema está imerso em ar ). Luz monocromática com comprimento de onda , incide sobre a camada de espessura com um ângulo de incidência pequeno.
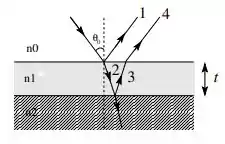
a) Determine as frequência e os comprimentos de onda da luz nos três meios.
b) Obtenha a mínima espessura da camada superior para que ela funcione como uma cama anti-reflexo (mínima reflexão) para este comprimento de onda em incidência normal.
c) Para a espessura calculada no item anterior, encontre os comprimentos de onda da luz visível () para os quais há um máximo de reflexão (interferência construtiva) para incidência normal.
Ver solução completaQuestão 44
A figura abaixo mostra um bloco de plástico transparente com índice de refração e espessura que varia continuamente entre (extremidade esquerda) e valor (extremidade direita). Um feixe de luz monocromática de comprimento de onda incide normalmente sobre toda a extensão do bloco e é refletida na direção do observador O. Ele observa o bloco numa visão superior e enxerga um perfil sequencial de interferência luminosa composta por 6 franjas escuras e 5 franjas claras ao longo da extensão do filme, onde as franjas nas extremidades são escuras. Considere a incidência normal dos raios de luz.
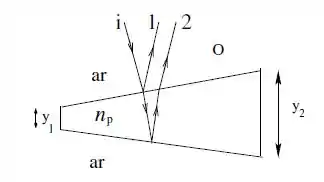
(a) Obtenha as condições para interferência construtiva e destrutiva da luz observada para uma dada espessura y tal que
(b) Calcule a diferença em termos de e
Ver solução completaQuestão 45
Em experimento com anéis de Newton o raio de curvatura R da lente é 5,0 m e seu diâmetro d vale 20 mm. O comprimento de onda é 589 nm. Admita que haja anéis de Newton até a borda da lente,
(a) Determine o número de anéis claros formados.
Ver solução completaQuestão 46
Uma película muito fina de material transparente, de índice de refração é utilizada como revestimento antirrefletor na superfície de um vidro de índice de refração de uma célula solar. Qual deve ser a espessura mínima da película para uma incidência perpendicular não ser observar por reflexão da luz que no vácuo tem comprimento de onda ?
Questão 47
O vidro de um carro, com índice de refração é coberto por fora por uma película fina com índice de refração tal que .
Uma luz monocromática proveniente do exterior do carro incide no vidro quase perpendicularmente ao mesmo.
Se é o comprimento de onda desta luz dentro da película, quão fina deve ser a película para que haja luz refletida?
(Considere a interferência entre os raios provenientes das superfícies ar-película e película-vidro)
- Nenhuma das anteriores
Questão 48
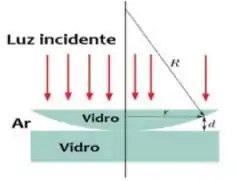
Um experimento com anéis de Newton é usado para determinar o raio de curvatura de uma lente plano-convexa. Incide-se luz com comprimento de onda λ = 670 nm perpendicularmente à face plana da lente. Formam- se diversos anéis claros e escuros para um observador situado ao lado da fonte luminosa. O raio do vigésimo anel escuro é11 mm. Calcule o raio R da lente.
Ver solução completaQuestão 49
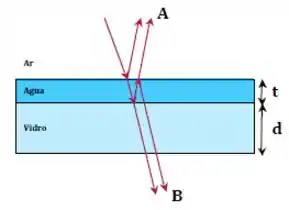
Um raio de luz monocromático incide quase perpendicularmente em um filme fino de água de espessura , sobre um bloco de vidro de espessura , conforme figura abaixo.
Dois observadores, e , determinam o critério para o qual a diferença de fase total, por reflexão e/ou caminho ótico percorrido dos raios emergentes, leve a uma interferência destrutiva.
Considere . De acordo com os observadores e , respectivamente, a interferência será destrutiva quando ( e são números inteiros positivos):
,
- e
- e
- e
- e
- e
- e
Questão 50
Coloque de falso ou de verdadeiro nas afirmações abaixo e justifique ambas as opções.
( ) O divergente do campo magnético não é nulo em um ponto do espaço dentro de uma bobina portadora de corrente elétrica dependente do tempo.
( ) O rotacional de um campo elétrico é nulo em um ponto do espaço vazio no interior de uma bobina portadora de uma corrente elétrica independente do tempo.
( ) Haverá interferência construtiva por reflexão em uma placa de vidro imersa em água quando iluminada normalmente à sua superfície por uma onda luminosa vinda da água ().
( ) Se colocarmos o dispositivo de Young (originalmente na água) imerso no ar, as franjas brilhantes se tornarão mais próximas.
Ver solução completaQuestão 51
(III) Um experimento com anéis de Newton é usado para determinar o raio de curvatura de uma lente. Incide-se luz com comprimento de onda λ = 546 nm perpendicularmente à face plana da lente. Formam-se diversos anéis claros e escuros alternados para um observador situado ao lado da fonte luminosa. O raio do anel claro de ordem m é = 0,162 cm e o raio do anel claro de ordem m + 20 é = 0,368 cm.
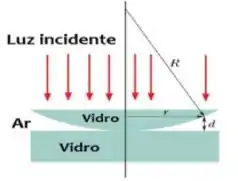
(c ) Calcule o raio R da lente.
Ver solução completaQuestão 52
– Observa-se o fenômeno da interferência em uma lâmina delgada de espessura e índice de refração ao ser iluminada com luz branca em incidência quase perpendicular à superfície.
A lâmina está imersa em água cujo índice de refração é menor que o da lâmina.
Determine a menor espessura da lâmina () para que a luz de comprimento de onda (referido ao vácuo) tenha uma reflexão intensa (máximo).
Ver solução completaQuestão 53
Uma película transparente de espessura e com índice de refração é iluminada normalmente por luz branca. A película está suspensa no ar (índice de refração ).
- A luz refletida nas duas superfícies da película interferem entre si. Obtenha a equação que determina os comprimentos de onda das ondas que interferem construtivamente.
- A luz visível é composta por ondas com comprimentos de onda entre e . Qual onda da luz visível interferirá construtivamente?
- A mesma película é imersa num líquido com índice de refração . Escreva a equação que determina os comprimentos de onda que interferem construtivamente.
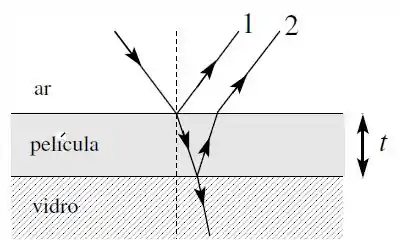
Questão 54
Uma película transparente de espessura e com índice de refração está colocada entre dois meios dielétricos: ar (índice de refração ) e vidro (índice de refração ). Luz branca incide quase normalmente sobre essa película e um observador vê a luz transmitida, conforme a figura. A luz branca tem comprimentos de onda entre e . Para quais comprimentos de onda neste intervalo haverá interferência construtiva entre os raios e da figura?