Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 2.Problemas - Ex. 6
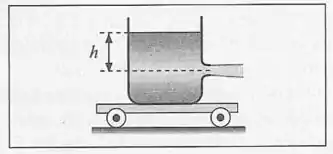
Um tanque de água encontra-se sobre um carinho que pode mover-se sobre um trilho horizontal com atrito desprezível. Há um pequeno orifício numa parede, a uma profunidade abaixo do nível da água no tanque. A área do orifício é (despreze o fator de contração da veia líquida), a massa inicial da água é e a massa do carrinho e do tanque é . Qual é a aceleração inicial do carrinho?
Passo 1
Vamos começar encontrando uma fórmula para a força que a água ejetada gera sobre o sistema quando é empurrada para fora: o empuxo.
Pela segunda lei de Newton, nós sabemos que a soma das forças externas agindo sobre um sistema é:
Onde é o momento linear. Nesse caso, não existem forças externas agindo, então:
Usando a regra do produto:
O empuxo é justamente a força associada à essa aceleração , então:
E podemos escrever a massa como produto da densidade da água e do volume no interior do tubo:
Como a densidade é uma constante, ficamos apenas com:
Passo 2
Agora vamos lembrar da fórmula para essa taxa de variação do volume (que é a vazão volumétrica):
Onde é a área do orifício por onde a água escapa e é a sua velocidade:
Agora vamos usar a equação de Bernoulli entre dois pontos. Um no topo da superfície do líquido e outro bem na saída do tubo.
A pressão nos dois pontos é igual, porque os dois estão em contato com a atmosfera:
E a velocidade no topo da superfície é nula:
Passo 3
Vamos substituir isso na fórmula que encontramos para o empuxo:
E como , a aceleração do sistema é:
E é a soma das massas da água, do carrinho e do tanque:
Resposta
A aceleração inicial do carrinho é .