Campos Cruzados
Teoria
Tanto um campo elétrico quanto um magnético podem exercer uma força sobre uma partícula com carga elétrica. Quando os dois campos são perpendiculares entre si, dizemos que se tratam de campos cruzados.
E agora, como é que será o movimento de uma carga na presença de campos cruzados? É isso que nós vamos ver agora!
Força Resultante Nula
Antes de começarmos, vale relembrar uma forma de representar vetores que vamos usar bastante aqui:
- Quando um vetor está entrando no plano da página, nós o representamos dessa forma
(é como se você estivesse vendo as penas de uma flecha que está entrando na página); - Quando um vetor está saindo do plano da página, nós o representamos dessa forma
(é como se você estivesse vendo a ponta de uma flecha que está saindo da página).
Vamos imaginar que uma partícula de carga está se movendo em uma região (entre duas placas carregadas) com a presença de um campo elétrico e de um campo magnético, de acordo com a seguinte situação:
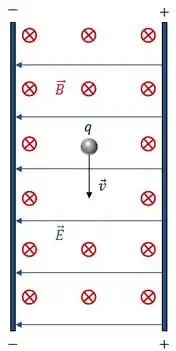
Supondo que (carga positiva), as forças sobre a carga vão ter essa cara:
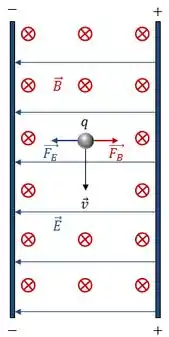
Agora, concorda comigo que se houver uma força resultante pra qualquer um dos lados, a trajetória da partícula carregada vai sofrer um desvio?
O único jeito da trajetória da partícula não sofrer nenhuma deflexão será se a força elétrica e a força magnética se cancelarem mutuamente, logo:
Finalmente:
Assim, quando temos uma situação de campos cruzados na qual as partículas não sofrem desvio de trajetória, podemos medir a velocidade das partículas.
Efeito Hall
Já sabemos que elétrons no vácuo podem ser desviados se estiverem sob a ação de um campo magnético. Mas será que isso se restringe somente para quando os elétrons estão no vácuo?
Não! Os elétrons que se movem no interior de um fio de cobre, por exemplo, também podem ser desviados por um campo magnético e esse efeito se chama Efeito Hall.
Vamos imaginar uma fita de cobre de largura , percorrida por uma corrente , cujo sentido é de cima para baixo (logo o dos elétrons é o contrário).
Quando um campo magnético B, que aponta para dentro da tela, é ligado, uma força magnética age sobre os elétrons, deslocando-os para o lado direito da fita, como na figura abaixo:
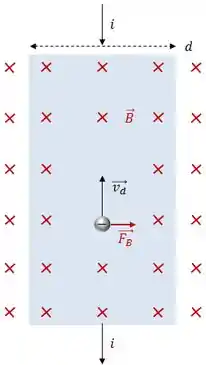
O acúmulo de elétrons no lado direito ocasiona uma separação de cargas, que, por sua vez, gera um campo elétrico (perpendicular ao magnético) no interior da fita.
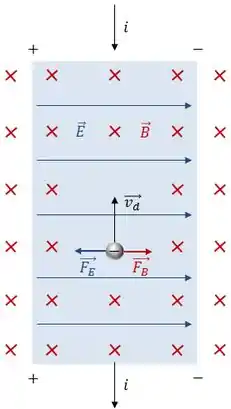
Os elétrons continuam a se mover até que a força elétrica exercida pelo campo se iguale a magnética. Nesse momento:
O campo elétrico gerado está associado a uma diferença de potencial, chamada diferença de potencial de Hall, dada por:
A velocidade de deriva é dada por:
Onde é o número de portadores de carga por unidade de volume. Misturando a coisa toda, podemos chegar a essa equação:
Onde é a espessura da fita, dada por:
É isso, galera. São essas as equações que precisamos saber para resolver qualquer exercício de Efeito Hall.
Agora vamos praticar?
Efeito Hall
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ- Física III-Prova 2-2014.1-Múltipla Escolha n°4.
Todas as partículas carregadas que passam através de uma região em que existem campos elétrico e magnético constantes, ortogonais, sem serem defletidas, têm em comum:
- A massa;
- O momento linear;
- A velocidade;
- A energia;
- A razão entre a carga e a massa;
Passo 1
Se elas não são defletidas quer dizer que a força resultante por elas é nula:
Portanto as duas forças (i.e. elétrica e magnética) em cada uma delas devem se anular:
Portanto os módulos serão iguais:
Passo 2
Como eles são ortogonais, seja a componente da velocidade que contribui para força magnética:
Ou seja, a velocidade tem sempre esse mesmo valor:
Ao passo que a carga pode ser qualquer coisa e a massa também.
Resposta
Letra c
Exercício Resolvido #2
UFRJ- Física III-Prova 2-2015.1-Múltipla Escolha n°3.
Uma região possui campo elétrico e magnético uniformes.
O campo elétrico aponta na direção e sentido de e o campo magnético aponta na direção e sentido de . Uma partícula de carga positiva atravessa a região em movimento retilíneo e uniforme. Em qual direção e sentido aponta a velocidade da partícula?
Passo 1
Para que a carga tenha movimento retilíneo uniforme é necessário que a força resultante sobre ela seja nula, sendo assim:
A força magnética é dada por e a força elétrica é dada por . Logo:
Passo 2
Sabemos que e . Assim:
Dessa forma, para que o produto vetorial aponte na direção e sentido de , usando a regra da mão direita, é necessário que o vetor velocidade tenha a direção e sentido de .
A resposta certa é a letra .
Resposta
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 226-13.
Uma fita de cobre com de espessura e de largura é submetida a um campo magnético uniforme de módulo , com perpendicular à fita.
Quando uma corrente atravessa a fita, uma diferença de potencial aparece entre suas bordas. Calcule . (A concentração de portadores de carga no cobre é .)
Passo 1
Sabemos que o número de portadores de carga por unidade de volume é:
Logo:
Onde:
Jogando esses caras na expressão de , teremos:
Resposta
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 226-14
Uma fita metálica com de comprimento, de largura e de espessura está se movendo com velocidade constante em uma região onde existe um campo magnético uniforme perpendicular à fita, como na figura abaixo:
A diferença de potencial entre os pontos e na fita é . Determine a velocidade escalar .
Passo 1
A velocidade está associada ao campo magnético e o campo elétrico pela relação:
Onde o campo elétrico é dado por:
Assim, a velocidade será dada por:
Onde:
Finalmente:
Resposta
Exercício Resolvido #5
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 225-7.
Na figura abaixo, um elétron acelerado a partir do repouso por uma diferença de potencial entra no espaço entre duas placas paralelas, separadas por uma distância , entre as quais existe uma diferença de potencial .
A placa inferior está a um potencial menor. Despreza o efeito de borda e suponha que o vetor velocidade do elétron é perpendicular ao vetor campo elétrico na região entre as placas.
Em termos dos vetores unitários, qual é o campo magnético uniforme para o qual a trajetória do elétron na região entre as placas é retilínea?
Passo 1
Então, primeiro vamos resumir esse enunciado: temos um elétron que é acelerado até entrar numa região que apresenta campos cruzados. Ele quer que a gente calcule o campo magnético para o qual o elétron não sofrerá desvio.
São dados: , , e a informação de que o vetor velocidade do elétron é perpendicular ao vetor campo elétrico na região entre as placas.
Passo 2
Beleza, vamos começar calculando o módulo do campo magnético. Para que a trajetória do elétron não sofra nenhum desvio, vimos que é necessário que:
O campo elétrico entre as placas é dado por:
Onde:
Portanto:
O problema é que não sabemos quanto vale a velocidade e não podemos usar essa mesma relação acima para a porque não sabemos a distância em que o elétron foi acelerado por esse potencial, então vamos ter que ir por outro caminho.
Passo 3
Para determinar a velocidade com que o elétron chega na região entre as placas, vamos usar a energia cinética do elétron. Oi?! Como assim?!
Se liga, a variação de energia cinética do elétron deve ser igual ao trabalho realizado sobre ele.
Logo:
Como o elétron parte do repouso, sua velocidade inicial é nula, portanto:
Onde:
Portanto:
Passo 4
Agora sim! O módulo do campo magnético será:
O próximo passo é determinar a direção e sentido do campo magnético... pra isso, vamos fazer uma análise vetorial.
Passo 5
Sabemos que o elétron se move na no sentido . Além disso, o enunciado disse que a placa superior possui um potencial maior, isso significa que o campo elétrico está no sentido , como mostra a figura abaixo.
Como se trata de um elétron (carga negativa), a força elétrica sobre ele estará apontando no sentido contrário do campo elétrico, logo, no sentido .
Já sabemos que, para o elétron não sofrer nenhuma deflexão na sua trajetória:
Isso quer dizer que a força magnética estará apontando no sentido .
Cara, vou ser sincero contigo... acho muito mais tranquilo usar a regra da mão direita aqui...
Nós sabemos que:
Assim, basta colocar o polegar no sentido de e o seu indicador no sentido de e vemos que o campo magnético deve estar no sentido . Só que como o elétron tem carga negativa, nosso resultado será o contrário, e o campo magnético na verdade estará no sentido .
Resposta
Exercício Resolvido #6
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 27.30, pp. 235.
Uma partícula com velocidade inicial entra em uma região com campos elétrico e magnético uniformes e perpendiculares entre si. O campo magnético na região é . Calcule o módulo, a direção e o sentido do campo elétrico na região, considerando que não haja desvio, para uma partícula de carga
- ;
Despreze o peso da partícula.
Passo 1
Como a partícula carregada não sofre nenhum desvio na região, então a força resultante sobre a partícula tem que ser nula, isto é,
Sendo
Substituindo as expressões para as forças elétrica e magnética
Simplificando essa expressão, temos
Então, olha só, a carga sumiu!! Isso significa que, independente do valor da carga, o vetor campo elétrico é dado por essa expressão. Colocando os vetores da velocidade e campo magnético dentro dessa expressão, temos que
onde usamos o seguinte resultado do produto vetorial .
Passo 2
b) Como vimos, o campo elétrico não depende do valor da carga e tem o mesmo módulo, direção e sentido que no caso anterior. Por isso, para este item também temos que
Resposta
Exercício Resolvido #7
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 27.51, pp. 237.
A Figura abaixo indica uma placa de prata com dimensões e e que produz uma corrente igual a no sentido . A placa está em repouso em um campo magnético uniforme na direção , cujo módulo é igual a . Sabendo que existem elétrons livres por metro cúbico, determine:
- o módulo da velocidade de arraste dos elétrons na direção do eixo ;
- o módulo, a direção e o sentido do campo elétrico no eixo produzido pelo efeito Hall ;
- a fem Hall.
Passo 1
a) Como a gente viu na teoria, a densidade de corrente na direção é dada por
Por outro lado, sabemos também que a densidade é a corrente por unidade de área. Por isso, podemos escrever também que
onde já usamos que a área por onde os elétrons fluem é , como está se pode ver na Figura, já que a corrente flui na direção e sentido do eixo .
Convertendo os valores necessários pro SI
E lembrando que a carga do elétron é
Colocando os valores dados no enunciado, temos
Passo 2
b) Como os elétrons estão caminhando na direção e sentido do eixo , então, a velocidade de arraste está na direção contrária, isto é,
Como o campo magnético é e a carga dos elétrons é negativa, temos que a força magnética é dada por
Portanto, a força magnética está ao longo do eixo . Nesse caso, então, a força elétrica deve estar no sentido do eixo . Como a força elétrica sobre os elétrons é dada por e essa força tem que ser igual a , o vetor campo elétrico tem que estar na direção do eixo .
Para encontrarmos o módulo de , temos que igualar a força elétrica com a força magnética. Isso dá para a gente o seguinte
O vetor campo elétrico é
Passo 3
c) Para fechar, a fem Hall, que está ao longo do eixo e é uma espécie de ddp ao longo da barra nessa direção, é dada por
Resposta
a)
b)
c)