Força Magnética
Produzido por Bruno SoaresTeoria
Fala aí, aqui é o Responde Aí, nós somos a solução para o seu semestre. Com a gente você estuda de forma clara, descontraída e arrebenta nas provas.
Estamos aqui hoje para falar pra você sobre um conceito muito importante dentro da magnetismo, a força magnética. Então, se você é aluno de engenharia, física e alguns outros cursos de exatas e está cursando uma disciplina que você precisa saber sobre magnetismo, não saia dessa página porque esse conteúdo é pra você.
Então, vem comigo!
A primeira coisa que precisamos entender sobre a força magnética é que ela atua apenas em corpos carregados e EM MOVIMENTO. Sempre que um corpo carregado em movimento entra em contato com um campo magnético surgirá sobre ele uma força magnética.
Para uma carga puntiforme, temos que a fómula da força magnética é a seguinte:
Onde:
é a força magnética; é a carga elétrica, em ; é a velocidade da carga, em ; é o campo magnético, expresso em , e; é o procuto vetorial entre o vetor velocidade e o vetor campo magnético
IMPORTANTE: A força magnética é expressa em
Note que a força magnética é um vetor, então ela tem um módulo, direção e sentido. Note também que ela é definida através de um produto vetorial, então para calcularmos o módulo, direção e sentido da força magnética precisamos calcular essas propriedades para um produto vetorial.
Vamos começar pelo módulo. Por definição, o módulo de um produto vetorial é dado pela multiplicação entre os módulos de cada vetor envolvido e o seno do ângulo formado entre esses vetores. Então:
Onde:
é o módulo do etor velocidade; é o módulo do vetor campo elétrico, e; é o ângulo formada entre os dois vetores.
Desse modo, podemos calcular o módulo da força magnética como:
E a direção e sentido?
A direção e sentido é dada pela regra da mão direita. Eu aconselho você a dar uma conferida nessa página nossa que explica bem bonitinho a regra da mão direita.
Mas, basicamente, para usar a regra da mão direita nesse caso da força magnética você vai fazer como mostra essa figura aqui:
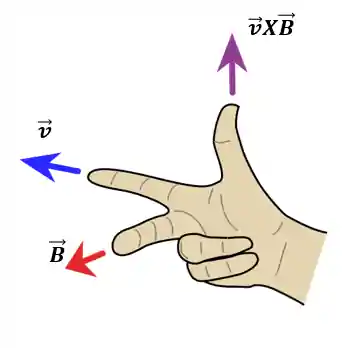
Você vai apontar o dedo indicador no sentido do vetor velocidade e o dedo médio no sentido do vetor campo magnético. A direção e sentido que o seu dedão apontar será a direção e sentido do produto vetorial entre esses dois vetores.
Uma coisa importante: Se a carga puntiforme tiver carregada positivamente, a força magnética terá a mesma direção e sentido dada pela regra da mão direita. Mas, se a carga for carregada negativamente, o sentido da força magnética será o inverso daquele indicado pela regra da mão direita. Então, no caso de carga negativa, você utiliza a regra da mão direita da mesma forma que falamos aí em cima e ao final inverte: se o dedão apontar para cima, a força magnética aponta para baixo e vice-versa.
Vídeos
Sim, nós temos esse conteúdo em vídeo, então se você é daqueles que gosta de uma boa aula e direto ao ponto é só conferir esse nosso vídeo aqui em baixo 👇🏾:
Nós temos também diversos exercícios resolvidos passo a passo em vídeo, vou deixar aqui em baixo um exercício em vídeo também para você ver como é o nosso estilo. Só confere 👇🏾: