Energia e Densidade de Energia em um Campo Magnético
Produzido por Bruno SoaresTeoria
Energia Armazenada em Indutores
A fórmula da energia armazenada num indutor é:
Onde é a indutância e é a corrente estacionária passando por ele.
Felizmente ao contrário do capacitor, não temos outras duas maneiras interessantes de interpretar isto. Esta é a melhor mesmo.
Não acredito que valha muito à pena colocar a demonstração deste fato aqui, mas qualquer coisa grita lá no botão vermelho.
Densidade de Energia do Campo Magnético
Da mesma maneira que o campo elétrico tinha uma energia associada à ele, o magnético também tem. A diferença é que o campo magnético não tem uma função potencial associada, ou seja, ele não é conservativo e não podemos falar de “energia potencial magnética”.
Dito isso, podemos decorar que a densidade de energia, ou seja, a energia guardada num elemento infinitesimal de espaço é:
E se quisermos achar a energia numa certa região, basta integrar. Não tem nenhuma novidade com relação à densidade de energia do campo elétrico. Mais uma vez, se quisermos achar a energia numa certa região, basta integrar na região:
Deixa eu te dar um mega bizu aqui: no geral ou esse campo magnético é uniforme (constante no espaço) ou ele tem simetria cilíndrica e depende só da distância radial (geralmente no exercício você vai ter que calcular antes o campo usando lei de Ampère, beleza?).
Se o campo for uniforme a integral fica
Ou seja, é só multiplicar a densidade de energia pelo volume!
Se o campo tiver simetria cilíndrica e depender da distância e supondo que estamos falando de um cilindro de comprimento vamos ter
Aqui eu vou deixar os limites de integração em aberto por que isso vai depender do problema que você estiver resolvendo! Se for só um cilindro de raio então os limites são de a , agora se for uma casca cilíndrica de raio interno e raio externo então vai ser uma integral de até .
Beleza! Vamo que vamo pros exercícios estourar a boca do balão! ;)
Densidade de Energia do Campo Magnético
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ – Física III – Prova 2 – 2012.1 – Múltipla Escolha nº5.
Considere as seguintes três afirmativas: (I) num dado circuito, a força eletromotriz auto induzida é sempre de sentido oposto ao da corrente total existente; (II) para um indutor dado, fixo, o trabalho realizado para estabelecer uma corrente de intensidade final através dele, desde um valor inicial nulo, é linearmente proporcional a , e (III) se, num dado ponto do espaço, simplesmente invertermos o vetor campo magnético, a densidade de energia associada ao campo magnético em tal ponto será quadruplicada. Qual(is) de tais afirmações está(estão) correta(s)?
- I
- II
- III
- I e II
- I e III
- II e III
- I, II e III
- Nenhuma
Passo 1
Analisando uma por uma: (I) num dado circuito, a força eletromotriz auto induzida é sempre de sentido oposto ao da corrente total existente;
Esta diz respeito à Lei de Faraday:
A fem auto induzida é oposta à variação de fluxo magnético. Então não, não é sempre de sentido oposto ao da corrente. A fem auto induzida vai tentar se opor à variação de fluxo somente. Digamos que a corrente esteja diminuindo: o fluxo pelo próprio circuito vai estar diminuindo também e a fem auto induzida vai ser no mesmo sentido da corrente para tentar ajudar.
Passo 2
A segunda afirmativa diz: (II) para um indutor dado, fixo, o trabalho realizado para estabelecer uma corrente de intensidade final através dele, desde um valor inicial nulo, é linearmente proporcional a ;
O trabalho para estabelecer uma corrente de intensidade num indutor (lembre que trabalho é igual energia) tem a expressão da energia armazenada nele:
Portanto não. Não é linearmente proporcional à corrente. É linearmente proporcional ao quadrado dela.
Passo 3
Por fim, a última diz: (III) se, num dado ponto do espaço, simplesmente invertermos o vetor campo magnético, a densidade de energia associada ao campo magnético em tal ponto será quadruplicada;
Esta diz respeito à densidade de energia num ponto:
Podemos ver que a densidade de energia num ponto só depende do módulo do campo neste ponto. Se invertermos o vetor, o módulo fica igual, portanto a energia também não se altera. Alternativa falsa.
Resposta
Letra h
Exercício Resolvido #2
UFRJ – Física III – Prova Final – 2014.1 – Múltipla Escolha nº2.
Sabe-se que, no interior de um cilindro (circular reto) de raio , existe um campo magnético , onde são as coordenadas cilíndricas usuais, é uma constante, e o eixo coincide com o eixo de simetria do cilindro.
A energia magnética armazenada no cilindro entre e é
Passo 1
A densidade de energia magnética é dada por:
Assim, a energia magnética é dada por:
Como estamos trabalhando com um cilindro e o campo magnético varia de acordo com a coordenada radia, o volume infinitesimal será dado por:
Logo:
Finalmente:
A resposta certa é a letra .
Resposta
Exercício Resolvido #3
UFRJ – Física III – Prova 2 – 2012.2 – Múltipla Escolha nº9.
Considere um campo magnético estacionário não uniforme dado por onde é a distância do ponto de aplicação do campo magnético até um determinado eixo, é o vetor unitário circular em torno de tal eixo, e . Qual opção indica a energia por unidade de comprimento ao longo do eixo, entre duas superfícies cilíndricas coaxiais com eixo supracitado, de raios e , com ?
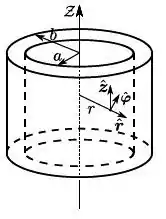
Passo 1
Aplicando a fórmula da densidade de energia do campo magnético:
Conseguimos a energia por comprimento se integramos na área da coroa circular:
Passo 2
Como já temos o campo, aplicando coordenadas polares (usando o macete de uma integral só):
Substituindo:
Resposta
Letra b
Exercício Resolvido #4
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 30.15, pp. 338
Um solenóide longo de comprimento e área de seção reta contém espiras circulares e transporta uma corrente de . Supondo que o campo magnético dentro do solenóide é uniforme, calcule:
- O campo magnético no solenóide;
- A densidade de energia no campo magnético, se o solenóide for preenchido com ar;
- A energia total contida no campo magnético da bobina;
- A auto-indutância do solenóide.
Passo 1
a) Esse exercício é bom porque a gente pode revisar, rapidinho, algumas coisas importantes sobre o campo magnético de um solenóide.
A primeira coisa é que, como esse solenóide é longo, ou seja, o comprimento dele é muito maior do que o diâmetro de cada espira, o campo magnético gerado pela corrente fica todo armazenado no interior do solenóide e tem o mesmo valor em todos os pontos lá dentro, por isso o enunciado fala que esse campo é uniforme.
A expressão para o módulo desse campo é
Substituindo os valores que o enunciado fornece, obtemos esse módulo é
Passo 2
b) A gente também viu na teoria que a região no interior dentro do solenóide, que armazena um campo magnético uniforme, contém uma energia devida à esse campo. O valor da densidade de energia acumulada dentro do campo magnético uniforme do solenóide é
Ou seja, cada metro cúbico da região no interior do solenóide armazena uma quantidade de energia de .
Passo 3
c) Bom, se cada do volume do interior do solenóide armazena de energia, para encontrar a energia total armazenada no volume de dentro do solenóide, a gente precisa multiplicar essa energia pela valor do volume total, que é dado por
Colocando tudo isso junto, a gente fica com
Esse é o valor da energia total armazenada no campo magnético uniforme no interior do solenóide.
Passo 4
d) Mas, agora, quero te ajudar a lembrar do seguinte: também podemos expressar a energia armazenada no campo magnético como
em que é chamada de auto-indutância do sistema. No caso do nosso exercício aqui, esse sistema com energia dentro é o solenóide, blz?
Daí, ficou tranquilo, né? Se a gente usa essa última expressão para a energia total, a auto-indutância é dada por
Resposta
Exercício Resolvido #5
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exemplo 28.6, pp. 338
Um solenóide toroidal cheio de ar, com campo magnético uniforme ao longo de toda a seção reta de seu núcleo, possui espiras e um raio médio de , com seção reta de área igual a . Supondo que a corrente que passa em suas espiras seja igual a , calcule:
- O campo magnético do toróide;
- A auto-indutância do toróide;
- A energia armazenada no campo magnético;
- A densidade de energia armazenada no campo magnético.
Passo 1
Vamos tentar entender a situação do problema dando uma olhada para a figura abaixo. Se você pegar a ideia dessa questão, você mata qualquer outro problema parecido que aparecer no seu caminho...vai por mim... :-) Fica firme!!
Aqui representei para você, para ficar mais fácil de a gente ver a situação, apenas uma seção transversal de um toróide, neste caso apenas metade do toróide e apenas algumas poucas das espiras quadradas (poderiam ser circulares também, ok? Não vai importar para o que a gente vai ver neste exercício!!!).
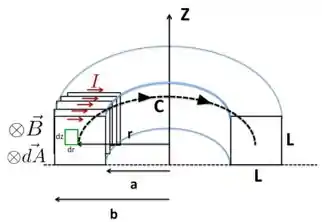
Cada uma das espiras transporta uma corrente e as colocamos no sentido horário indicado na figura. Além disso, imagina que essas espiras estão todas muuuiiitoo próximas umas das outras, o que geralmente aparece nos textos como “espiras muito compactas”.
Pela regra da mão direita, a gente sabe que o campo magnético que essas correntes geram está entrando no plano da página e esse campo fica todo dentro da região de raio . Para facilitar nossa discussão, colocamos também a área sempre paralela ao campo magnético e entrando no plano da página, como ilustrado na figura.
Passo 2
a) Lá na nossa discussão da teoria, você viu que o módulo para o campo magnético dentro do toróide tem a seguinte expressão
Fica claro dessa equação, que o campo magnético depende da distância do centro do toróide, ou seja, posições diferentes dentro das espiras tem valores diferentes para o campo magnético, blz?
Agora, existe uma situação particular, que vou te mostrar agora. Quando a gente tem , ou seja, a seção reta tem dimensões muito pequenas comparadas com a distância , a gente tem um campo uniforme dentro do toróide e podemos substituir a distância por um raio médio fixo. Isto é, na expressão do campo, podemos fazer o seguinte
que tem um valor constante e igual a em todos os pontos dentro do toróide. Fechou?? Se você substitui os valores dados no enunciado, obtém que o campo tem o valor de
Tudo que a gente vai fazer nos próximos itens vai usar esse campo constante com aí de cima. Fica ligado nisso, tá ok?
Passo 3
b) Bom, agora que já visualizamos a questão através da figura (tomara que ela tenha mesmo te ajudado com isso...rsrs), vamos entender o que precisamos calcular neste caso.
Primeiro, para obter a autoindutância do toróide, vamos começar nossa solução pela expressão do fluxo magnético e sua relação com a autoindutância dada por
sendo que é corrente que percorre cada uma das espiras do solenóide toroidal.
O caminho que a gente vai seguir abaixo é o seguinte: calculamos o fluxo total do toróide e o igualamos a para tirar a expressão para . Sacô a ideia? Segue firme...
Tendo o valor do campo gerado pela corrente que passa nas espiras, podemos encontrar o fluxo magnético. Como o vetor área é sempre paralelo a , temos que
Agora, lembra lá do enunciado que o campo é uniforme dentro do toróide? Por essa razão, a gente pode tirar o campo magnético dessa integral e já substituir o valor que temos para ele do Passo 2. Isso dá o seguinte
que nos permite encontrar a expressão para a autoindutância do toróide como
Fica ligado, porque essa expressão vale apenas para o caso em que o campo magnético dentro do toróide é uniforme, tranquilo? Guarda isso no coração...Quando não for uniforme, daí a gente vai ter que trabalhar um pouco mais, mas a gente vai te ajudar nesse caso mais geral também, já que pode cair também na sua prova...
Finalizando o item, colocamos os valores do enunciado nessa expressão e tacando na calculadora, você vai ter que
Passo 4
c) Como a energia magnética acumulada no campo magnético é dada por
temos, utilizando o valor da indutância encontrada no passo anterior, que
Passo 5
e) A energia que encontramos no passo anterior fica armazenada em um volume igual ao produto da área da seção reta do toróide vezes o comprimento do toróide que igual a , ou seja, .
Portanto, a densidade de energia, ou seja, a energia por unidade de volume, tem o seguinte valor
Esse valor diz para a gente que cada do interior do toróide tem uma energia de .
Resposta
Exercício Resolvido #6
UFRJ- Física 3 - PF 2017.2 - DIURNO – 14 - Adaptada
Um solenóide toroidal tem seção transversal quadrada de lado , raio interno , raio externo e voltas de um fio condutor fino enroladas de forma compacta em torno dele. Por cada uma das espiras passa uma corrente , que produz um campo magnético no interior desse toróide. Nessa situação e sabendo que esse campo magnético não é uniforme ao longo da seção reta de cada espira, qual é a energia magnética acumulada na região interna desse toróide?
Passo 1
Vamos tentar entender a situação do problema olhando para a figura abaixo. Representamos apenas uma seção transversal de um toróide, neste caso apenas metade do toróide e apenas algumas das espiras quadradas. Cada uma das espiras quadradas transporta uma corrente e as colocamos no sentido horário indicado na figura.
Por isso, pela regra da mão direita, o campo magnético que essas correntes geram está entrando no plano da página. Para facilitar nossa discussão, colocamos também a área sempre paralela ao campo magnético , como ilustrado na figura. Colocamos também uma área infinitesimal pela qual o campo passará.
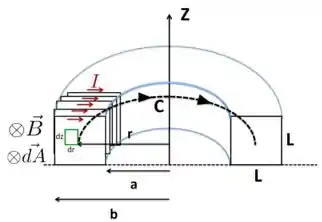
A corrente em cada uma das espiras atravessará uma área definida pelo contorno fechado , que está a uma distância do eixo .
Passo 2
Bom, agora que já visualizamos a questão através da figura (assim espero...rsrs), vamos entender o que precisamos calcular neste caso.
Primeiro, para obter a autoindutância , vamos começar nossa solução pela expressão do fluxo magnético e sua relação com a autoindutância de acordo com
sendo que é corrente que percorre cada uma das espiras quadradas do solenóide toroidal.
O caminho que a gente vai seguir abaixo é o seguinte: calculamos o fluxo total do toróide e o igualamos a para tirar a expressão para .
Então, obtemos o seguinte módulo para o campo magnético
Tendo o valor do campo gerado pela corrente que passa nas espiras, podemos encontrar o fluxo magnético. Como o elemento de área é sempre paralelo a e este tem mesmo valor em todos os pontos da curva neste caso, temos que
Como o módulo do campo magnético não é uniforme dentro do toróide, pois depende da distância como acabamos de ver, então não podemos tirar o de dentro da integral, blz?? Fica ligado nessa informação... Sei que a gente fica tentado em tirar o da integral porque facilita e muito nossa vida, mas não faça isso a menos que o enunciado te diga que é uniforme...IMPORTANTÍSSIMO ISSO...
Dá uma olhada lá na figura e veja que, neste sistema de coordenadas, o elemento infinitesimal de área atravessada pelo campo é . Por isso, o fluxo total é
Resolvendo a integral acima, obtemos que o fluxo magnético total através das espiras é
que nos permite encontrar a expressão para a autoindutância.
Passo 3
Como a energia magnética acumulada no campo magnético é dada por
temos, utilizando a expressão da indutância encontrada no passo anterior, que
Resposta
Exercício Resolvido #7
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 9ª edição. Rio de Janeiro: LTC, 2012, pp 283
Um solenoide tem 85,0 cm de comprimento, uma seção reta de 17,0 cm², 950 espiras e é percorrido por uma corrente de 6,60 A. (a) Calcule a densidade de energia do campo magnético no interior do solenoide. (b) Determine a energia total armazenada no campo magnético, desprezando os efeitos de borda.
Passo 1
Para resolvermos a letra (a) vamos utilizar a fómula de densidade de energia do campo magnético:
Como o campo magnético no interior de um solenoide é dado por:
Sendo que é a corrente passando pelo solenoide e é o número de espiras por unidade de comprimento.
Temos:
Juntando tudo temos:
Passo 2
Para resolvermos a letra (b) temos que lembrar que o campo magnético no interior do solenoide ideal é uniforme. Portanto, a energia total armazenada no campo magnético é dada pela fórmula:
Podemos tirar o campo magnético da integral pois ele é uniforme. A integral tripla de dV é igual ao volume total do solenoide. O volume é dado pelo produto da área da seção reta pelo comprimento do solenoide.
Temos que a área é:
Sendo assim:
Resposta
(a)
(b)
Exercício Resolvido #8
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 9ª edição. Rio de Janeiro: LTC, 2012, pp 283
Um indutor toroidal com uma indutância de 90,0 mH envolve um volume de 0,0200 m³. Se a densidade de energia média no toroide é 70,0 J/m3, qual é a corrente no indutor?
Passo 1
Para resolvermos essa questão vamos utilizar a fórmula da energia armazenada num indutor:
Onde é a indutância, e é a corrente passando por ele.
Mas o exercício dá a densidade de energia e nós precisamos da energia. A fórmula que relaciona essas duas grandezas é a seguinte:
Sendo V o volume do solenoide.
Passo 2
Rearranjando as equações vamos ter: