Exercícios de Energia e Densidade de Energia em um Campo Magnético - Lista de Exercícios Resolvida
Questão 1
Um solenóide longo de comprimento e área de seção reta contém espiras circulares e transporta uma corrente de . Supondo que o campo magnético dentro do solenóide é uniforme, calcule:
- O campo magnético no solenóide;
- A densidade de energia no campo magnético, se o solenóide for preenchido com ar;
- A energia total contida no campo magnético da bobina;
- A auto-indutância do solenóide.
Questão 2
Um solenóide toroidal cheio de ar, com campo magnético uniforme ao longo de toda a seção reta de seu núcleo, possui espiras e um raio médio de , com seção reta de área igual a . Supondo que a corrente que passa em suas espiras seja igual a , calcule:
- O campo magnético do toróide;
- A auto-indutância do toróide;
- A energia armazenada no campo magnético;
- A densidade de energia armazenada no campo magnético.
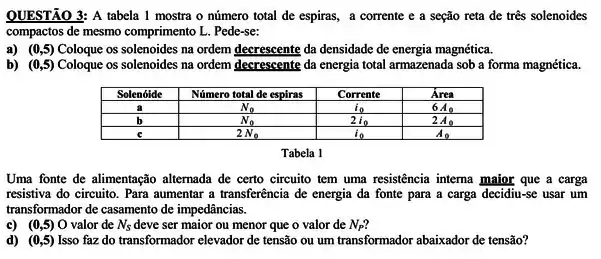
Questão 3
Um solenoide tem 85,0 cm de comprimento, uma seção reta de 17,0 cm², 950 espiras e é percorrido por uma corrente de 6,60 A. (a) Calcule a densidade de energia do campo magnético no interior do solenoide. (b) Determine a energia total armazenada no campo magnético, desprezando os efeitos de borda.
Ver solução completaQuestão 4
Um indutor toroidal com uma indutância de 90,0 mH envolve um volume de 0,0200 m³. Se a densidade de energia média no toroide é 70,0 J/m3, qual é a corrente no indutor?
Ver solução completaQuestão 5
Considere as seguintes três afirmativas: (I) num dado circuito, a força eletromotriz auto induzida é sempre de sentido oposto ao da corrente total existente; (II) para um indutor dado, fixo, o trabalho realizado para estabelecer uma corrente de intensidade final através dele, desde um valor inicial nulo, é linearmente proporcional a , e (III) se, num dado ponto do espaço, simplesmente invertermos o vetor campo magnético, a densidade de energia associada ao campo magnético em tal ponto será quadruplicada. Qual(is) de tais afirmações está(estão) correta(s)?
- I
- II
- III
- I e II
- I e III
- II e III
- I, II e III
- Nenhuma
Questão 6
Um solenóide toroidal tem seção transversal quadrada de lado , raio interno , raio externo e voltas de um fio condutor fino enroladas de forma compacta em torno dele. Por cada uma das espiras passa uma corrente , que produz um campo magnético no interior desse toróide. Nessa situação e sabendo que esse campo magnético não é uniforme ao longo da seção reta de cada espira, qual é a energia magnética acumulada na região interna desse toróide?
Ver solução completaQuestão 7
Considere um campo magnético estacionário não uniforme dado por onde é a distância do ponto de aplicação do campo magnético até um determinado eixo, é o vetor unitário circular em torno de tal eixo, e . Qual opção indica a energia por unidade de comprimento ao longo do eixo, entre duas superfícies cilíndricas coaxiais com eixo supracitado, de raios e , com ?
Questão 8
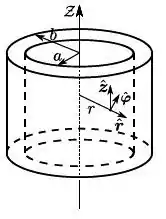
Sabe-se que, no interior de um cilindro (circular reto) de raio , existe um campo magnético , onde são as coordenadas cilíndricas usuais, é uma constante, e o eixo coincide com o eixo de simetria do cilindro.
A energia magnética armazenada no cilindro entre e é
Ver solução completa
Questão 9
Uma distribuição de corrente é dada pelo vetor densidade de corrente, em coordenadas cilíndricas, definido por:
para
, para ,
Onde é uma distância, e é uma constante positiva.
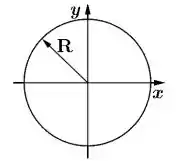
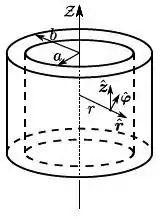
- Tomando como referência a figura ao lado, o campo magnético gerado pela densidade de corrente tem sentido horário ou anti-horário?
b) Encontre o módulo do campo magnético gerado pela densidade de corrente nas regiões e .
Ver solução completaQuestão 10
Considere um campo magnético estacionário não uniforme dado por onde é a distância do ponto de aplicação do campo magnético até um determinado eixo, é o vetor unitário circular em torno de tal eixo, e . Qual opção indica a energia por unidade de comprimento ao longo do eixo, entre duas superfícies cilíndricas coaxiais com eixo supracitado, de raios e , com ?
Questão 11
Sabe-se que, no interior de um cilindro (circular reto) de raio , existe um campo magnético , onde são as coordenadas cilíndricas usuais, é uma constante, e o eixo coincide com o eixo de simetria do cilindro.
A energia magnética armazenada no cilindro entre e é
Ver solução completa
Questão 12
A seguinte afirmação é verdadeira ou falsa: “Classicamente, os extremos de uma agulha ferromagnética podem ser representados como polos magnéticos. Na presença de um campo magnético externo, a energia magnética mínima se estabelece quando a agulha está na direção do campo magnético e, o sentido do polo norte para o sul da agulha aponta no mesmo sentido do campo magnético”.
Ver solução completaQuestão 13
Um circuito LC funciona como um oscilador eletromagnético ideal com frequência angular e energia total . Se representa a carga máxima no capacitor e a corrente máxima que circula no circuito, é CORRETO afirmar que:
Quando a carga no capacitor for nula, a energia acumulada no indutor será .
Quando a corrente for , a carga no capacitor será .
A carga máxima no capacitor vale .
A corrente máxima que circula no circuito é .
A diferença de potencial no indutor é máxima quando a corrente é .
Ver solução completaQuestão 14
No circuito da figura abaixo, a chave ficou na posição por um tempo muito longo.
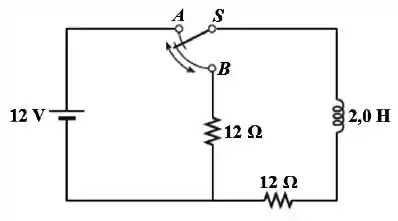
Nesta condição, qual é a corrente no circuito?
Agora, é subitamente movida de para em .
Calcule a inicial através do indutor e através de cada resistor.
Calcule a energia magnética inicial armazenada no indutor.
Calcule a energia total dissipada nos resistores.
Ver solução completaQuestão 15
Considere um cilindro longo de raio , o qual possui uma densidade volumétrica de carga , onde é uma constante e é uma distância radial até o eixo central do cilindro. Para qual distância radial no exterior do cilindro () o campo elétrico possui o mesmo valor do campo em ? (Expresse o resultado em função de ).
Ver solução completaQuestão 16
A figura abaixo ilustra duas cascas cilíndricas coaxiais e muito longas (podem ser consideradas infinitas), uma de raio e outra de raio .
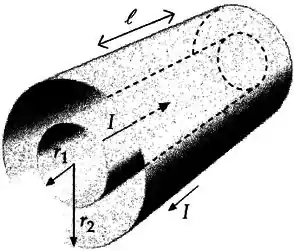
A corrente elétrica que passa em ambas as cascas cilíndricas tem intensidade , mas flui em sentidos opostos, como indicado na figura.
Para tal situação, calcule:
O módulo do campo magnético para , usando lei de Ampère.
A energia magnética armazenada num volume de comprimento na região entre as cascas.
A indutância por unidade de comprimento do sistema.
Ver solução completaQuestão 17
Uma bobina é ligada em série com um resistor de . Uma fonte ideal de é ligada aos terminais do conjunto e a corrente atinge um valor de após . (a) Determine a indutância da bobina. (b) Determine a energia armazenada na bobina nesse instante.
Ver solução completaQuestão 18
Uma bobina com uma indutância de e uma resistência de são ligadas bruscamente a uma fonte ideal com . Um décimo de segundo após ser feita a ligação, determine (a) a taxa com a qual a energia está sendo armazenada no campo magnético da bobina; (b) a potência dissipada na resistência; (c) a potência fornecida pela fonte.
Ver solução completaQuestão 19
No instante , uma bateria é ligada em série a um resistor e um indutor. Se a constante de tempo indutiva é , em instante a taxa com a qual a energia é dissipada no resistor é igual a taxa com a qual a energia é armazenada no campo magnético do indutor?
Ver solução completaQuestão 21
Considere o mesmo cabo coaxial da questão anterior.
Utilizando o campo calculado na questão anterior, determine a densidade de energia na região entre o cilindro e a casca.
Ver solução completaQuestão 22
Considere o mesmo cabo coaxial da questão anterior.
Obtenha a energia total armazenada pelo campo magnético em uma porção de comprimento desta região. Sugestão: utilize como elemento de volume para integração uma casca cilíndrica de raio e espessura infinitesimal ds.
Ver solução completaQuestão 23
Considere as seguintes três afirmativas: (I) num dado circuito, a força eletromotriz auto induzida é sempre de sentido oposto ao da corrente total existente; (II) para um indutor dado, fixo, o trabalho realizado para estabelecer uma corrente de intensidade final através dele, desde um valor inicial nulo, é linearmente proporcional a , e (III) se, num dado ponto do espaço, simplesmente invertermos o vetor campo magnético, a densidade de energia associada ao campo magnético em tal ponto será quadruplicada. Qual(is) de tais afimações está(estão) correta(s)?
- I
- II
- III
- I e II
- I e III
- II e III
- I, II e III
- Nenhuma
Questão 24
Considere o mesmo cabo coaxial da questão anterior.
A partir do resultado acima, obtenha a auto-indutância por unidade de comprimento deste cabo. Compare com o resultado obtido na questão anterior.
Ver solução completa