Indução, Energia e Potência
Produzido por Bruno SoaresTeoria
Introdução
De acordo com a Lei de Lenz, quando um imã é aproximado ou afastado de uma espira, uma força magnética “do contra” vai tentar resistir ao movimento.
Então, se quisermos que esse movimento continue sendo executado, teremos que realizar um trabalho, faz sentido?
Vamos dar uma olhada numa espira retangular, onde parte dela está imersa num campo magnético e ela se move para a esquerda.
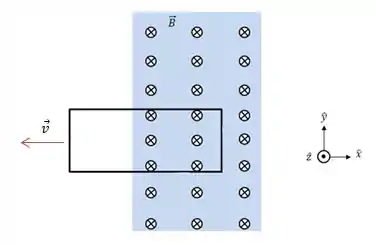
À medida que a espira vai para a esquerda, o fluxo magnético pela espira diminui, afinal a área atravessada pelo campo vai diminuindo.
Por conta da variação do fluxo, uma corrente é induzida na espira, e como o campo está entrando na página e o fluxo diminui, pela Lei de Lenz a corrente percorre o sentido horário na espira.
Essa corrente percorrendo a espira na presença de um campo magnético, faz com que apareça 3 forças na espira, e como queremos deslocar a espira para a esquerda com velocidade contante, é necessária uma quarta força capaz de deslocar a espira.
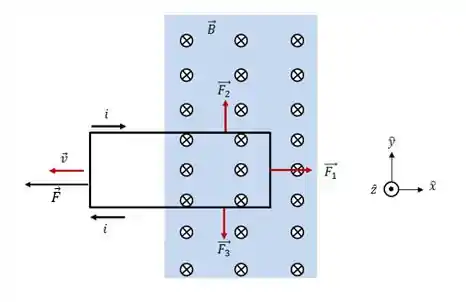
Teremos duas energias nesse sistema: A energia térmica que é produzida quando a corrente passa pela resistência da espira e a energia mecânica que é resultado do movimento da espira.
A treta aqui é que a energia mecânica transferida ao sistema espira é transformada na energia térmica dissipada na espira, então as duas energias serão iguais. Logo, quanto mais energia for transferida ao sistema, maior será a energia térmica dissipada.
Da mesma forma, a potência transferida ao sistema pela força, deve ser igual à potência elétrica dissipada na resistência.
Ok, vamos colocar isso em prática em uma situação bem comum de aparecer que é de uma espira com velocidade constante.
Então vamos calcular uma potência de cada vez, ok?
Potência Transferida ao Sistema
A energia transferida ao sistema é a energia mecânica, sendo assim a potência transferida ao sistema pode ser calculada da seguinte forma:
Nesse caso precisamos encontrar a força que é capaz de deslocar a espira pra esquerda com velocidade constante.
Para que a espira se mova com velocidade constante, o somatório de forças na espira deve ser nulo, e para facilitar podemos analisar isso apenas pro eixo do movimento.
Vamos analisar a imagem da espira e ver quais forças atuam:
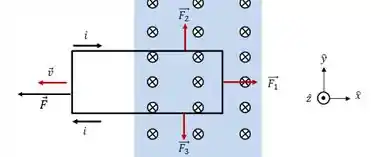
Para ter velocidade constante o somatório das forças em cada eixo precisa ser nulo também, portanto para o eixo temos:
A força é a força magnética aplicada à parte retilínea vertical da espira:
Como e são perpendiculares:
Para esse tipo de problema, enquanto a espira está entrando na região com campo magnético, a é dada pelo fluxo desse campo através da área da espira ao longo do tempo:
Onde o fluxo magnético através da área da espira é dado por:
E a área da espira é dada por:
Onde é a largura vertical da espira e é o comprimento variável da espira que está imersa no campo magnético.
Então temos:
Podemos passar o campo e o comprimento fixo para fora da derivada e deixar dentro dela só o que varia.
E como a velocidade é dada por:
Temos enfim a induzida:
Continuando, a corrente induzida será:
Onde é a resistência elétrica da espira.
A força aplicada à espira será:
Finalmente, a potência transferida ao sistema, será:
Potência Elétrica Dissipada
A potência dissipada na resistência da espira é dada por:
Como já vimos, a corrente induzida nesse tipo de situação é:
Jogando a expressão da corrente na fórmula da potência, teremos:
Isso demonstra exatamente o que eu te disse no início do capítulo, a potência transferida ao sistema pela força, deve ser igual à potência elétrica dissipada na resistência.
E essa potência vale:
Potência Transferida ao Sistema
Potência Elétrica Dissipada
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 296-29.
Se de um fio de cobre com de diâmetro são usados para formar uma espira circular, que é mantida perpendicular a um campo magnético uniforme que está aumentando a uma taxa constante de , qual é a taxa com a qual é gerada energia térmica na espira?Dado:
Passo 1
Quando o enunciado fala coisas do tipo “taxa de energia térmica gerada na espira”, na verdade ele quer dizer potência dissipada na espira.
Essa potência é dada por:
Vamos começar calculando a induzida, beleza?
Passo 2
Pela Lei de Faraday:
Como a área é constante, e o campo magnético é uniforme, podemos reescrever esse cara como:
Só precisamos saber calcular essa área direito... o comprimento do fio e o diâmetro dele. A área da espira é dada por:
O raio da espira está relacionado com o comprimento do fio através da relação:
Logo, a área será dada por:
Assim, a induzida será:
Passo 3
A resistência, por sua vez, será dada por:
Onde:
Logo:
Passo 4
Agora sim, a potência será dada por:
Eita! Vamos dar uma organizada nisso:
Onde:
Logo:
Resposta
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 296-30.
Uma antena em forma de espira, com uma área de e uma resistência de , é mantida perpendicular a um campo magnético uniforme de módulo . O módulo do campo diminui para zero em .
Qual é a energia térmica produzida na espira pela variação do campo?
Passo 1
A energia térmica produzida na espira pode ser calculada através da potência dissipada, portanto:
Onde:
Logo:
Passo 2
Pela Lei de Faraday:
Como a área é constante, o campo magnético é uniforme e perpendicular ao plano da espira:
Passo 3
Substituindo na expressão da energia, teremos:
Como o campo varia linearmente com o tempo:
Logo:
Onde:
Substituindo os termos, teremos:
Resposta
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 296-31.
Na figura abaixo, uma barra de metal é forçada a se mover com velocidade constante ao longo de dois trilhos paralelos ligados em uma das extremidades por uma viga de metal.
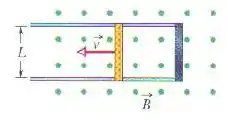
Um campo magnético de módulo aponta para fora da tela.
Se a distância entre os trilhos é e a velocidade escalar da barra é , qual é o valor absoluto da força eletromotriz gerada?
Se a barra tem uma resistência de e a resistência dos trilhos e da fita de ligação é desprezível, qual é a corrente na barra?
Qual é a taxa com a qual a energia é transformada em energia térmica?
Passo 1
Se a distância entre os trilhos é e a velocidade escalar da barra é , qual é o valor absoluto da força eletromotriz gerada?
Esse é um problema clássico de haste deslizante. Para esse caso, a induzida é dada por:
Onde:
Logo:
Passo 2
Se a barra tem uma resistência de e a resistência dos trilhos e da fita de ligação é desprezível, qual é a corrente na barra?
Bom, já temos e a resistência... agora a nossa vida ficou fácil.
Passo 3
Qual é a taxa com a qual a energia é transformada em energia térmica?
A taxa de geração de energia térmica é a potência dissipada na barra, logo:
Resposta
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 9ª edição. Rio de Janeiro: LTC, 2012, pp 280
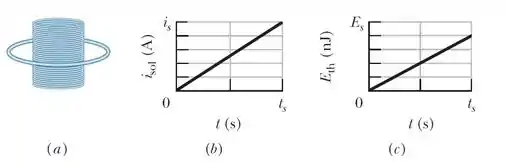
A figura abaixo mostra , em (a), uma espira circular concêntrica com um solenoide e está em um plano perpendicular ao eixo central do solenoide. A espira tem 6,00 cm de raio. O solenoide tem um raio de 2,00 cm, possui 8000 espiras/m e a corrente varia com o tempo da forma indicada na figura, em (b), onde a escala do eixo vertical é definida por e a escala do eixo horizontal é definida por . A figuramostra, em (c), em função do tempo, a energia que é transformada em energia térmica na espira; a escala do eixo vertical é definida por . Qual é a resistência da espira?
Passo 1
Bom, esse problema é um pouco complexo, devido a quantidade de informações, mas vamos com calma!
Primeiramente temos que perceber que se trata de uma questão sobre lei de Faraday. A corrente varia com o tempo e por causa diss, o fluxo do campo magnético vai variar também, e isso vai induzir uma força eletromotriz na espira.
Vamos lembrar da fórmula da lei de Faraday:
Como essa questão não pergunta nada sobre o sentido da força eletromotriz induzida, nem de sua corrente, eu vou suprimir esse sinal de menos da equação.
Mas:
Como no nosso problema a espira está posicionada em um plano perpendicular ao eixo central do solenoide:
E então:
Agora precisamos lembrar que o campo magnético no interior de um solenoide é dado pela fórmula:
Sendo que é a corrente passando pelo solenoide e é o número de espiras por unidade de comprimento.
Obs.: o campo magnético do lado de fora do solenoide é zero!
Entao ficamos com:
Vamos dar nome aos bois:
: força eletromotriz induzida;
: área do solenoide;
: permeabilidade magnética do vácuo, com valor
: corrente elétrica no solenoide;
: tempo.
Passo 2
Agora vamos avaliar o que diz a figura (b).
Na figura (b) temos que
Sendo e
Substituindo na formula:
Passo 3
Agora vamos lembrar das equações lá de circuitos com resistores envolvendo a taxa de dissipação da energia elétrica devido a uma resistência:
Temos duas:
Como nós temos o valor da força eletromotriz induzida na espira mas não temos a corrente induzida na espira, vamos utilizar a segunda fórmula:
Rearranjando:
Agora precisamos achar a potência, ou seja, uma taxa de energia por tempo.
Passo 4
Agora vamos avaliar o que diz a figura (c).
Na figura (c) temos que .
Repara que a a escala é dividida em 5 partes mas a reta só vai até a quarta parte, ou seja, da escala total de 100 nJ, que é 80 nJ. Fica ligado!
Voltamos a nossa formula:
Resposta
Exercício Resolvido #5
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 9ª edição. Rio de Janeiro: LTC, 2012, pp 280
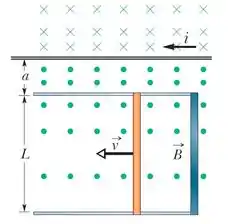
A figura mostra uma barra de comprimento que é forçada a se mover com velocidade escalar constante ao longo de trilhos horizontais. A barra, os trilhos e a fita metálica na extremidade direita dos trilhos formam uma espira condutora. A barra tem uma resistência de 0,400 Ω; a resistência do resto da espira é desprezível. Uma corrente que percorre um fio longo situado a uma distância da espira
produz um campo magnético (não uniforme) que atravessa a espira. Determine (a) a força eletromotriz e (b) a corrente induzida da espira. (c) Qual é a potência dissipada na espira? (d) Qual é o módulo da força que deve ser aplicada à espira para que se mova com velocidade constante? (e) Qual é a taxa com a qual a força realiza trabalho sobre a espira?
Passo 1
Vamos por partes pois o exercício é longo e envolve uma série de conceitos.
Como o exercício está falando de uma espira variando o seu tamanho (área), podemos admitir que se trata de um exercício sobre lei de Faraday.
Primeiro vamos calcular a força eletromotriz induzida:
Vamos chamar a distância entre a barra e a extremidade direita dos trilhos.
Presisamos lembrar da fórmula do campo magnético gerado por um fio em um ponto do espaço:
Sendo a distância entre o ponto e o fio; a corrente no fio e a permeabilidade magnética no vácuo.
Agora vamos considerar uma tira horizontal (paralela ao fio) infinitesimal de comprimento e largura , situada a uma distância r do fio. A área desta tira é: .
Então o fluxo através da tira é:
Como precisamos do fluxo total na área envolvida pela espira formada pela barra e pelos trilhos, temos:
De acordo com a lei de Faraday, a força eletromotriz induzida na espira é:
A única variável que depende do tempo, neste caso, é:
Sabemos lá da física 1 que nada mais é do que a velocidade:
Entao:
Substituindo:
Essa foi a letra (a)! Vamos continuar!
Passo 2
Para encontrarmos a corrente induzida na espira, precisamos lembrar da lei de Ohm:
Ou:
Com as variáveis do problema:
Substituindo:
Agora precisamos descobrir o sentido desta corrente:
Como a barra está se movimentando para a esquerda, a área da espira está aumentando. Portanto, o fluxo do campo magnético também está aumentando.
Pela lei de Faraday, a corrente induzida na espira terá o sentido oposto à essa variação do fluxo do campo magnético. Como o campo magnético está saindo do papel na área da espira, a corrente induzida irá gerar um campo magnético no sentido contrario, ou seja, entrando no papel. Pela regra da mao direita, se o nosso polegar aponta no sentido de entrar na folha, nossos dedos fazem o movimento no sentido horário.
Passo 3
Para resolver a letra (c), precisamos lembrar da fórmula da potência dissipada num resistor (que nesse caso é a resistência da espira):
Substituindo:
Passo 4
Para resolver a letra (d), precisamos considerar que para que a barra se mova com velocidade constante, a resultante das forças que agem sobre a barra deve ser nula. Para isso, a força externa aplicada à barra deve ser igual, em módulo, à força magnética e deve ter o sentido oposto. O módulo da força magnética exercida sobre um segmento infinitesimal da barra de comprimento , situado a uma distância do fio, é
Integrando a força magnética sobre toda a barra:
Substituindo:
Temos que:
Como o campo produzido pelo fio aponta para fora do papel na região onde a barra está se movendo e o sentido da corrente na barra é para cima, a força associada ao campo magnético aponta para a direita (pela regra da mão direita) e, portanto, a força externa aplicada deve apontar para a esquerda.
Passo 5
Finalmente, para resolver a letra (e), precisamos lembrar lá de física 1 que a taxa com que uma força externa realiza trabalho é dada pela fórmula:
Sendo a potência (taxa de energia de trabalho por segundo); a força e a velocidade.
Substituindo:
Como toda a energia fornecida pela força externa é convertida em energia térmica, este valor é igual ao da potência dissipada na espira, calculada na letra (c).
Resposta
(a)
(b) , sentido horário.
(c)
(d)
(e)