Fluxo Magnético
Produzido por Bruno SoaresTeoria
Fala aí, bem vindo ao RespondeAí! Ta aprendendo tudo direitinho de Física III? Já sabe o que é Campo Magnético e Força Magnética? Lei de Biot-Savart? Lei de Ampére? Caramba quanto nome estranho, mas relaxa que aqui no nosso site temos todos esse tópicos ensinados de maneira didática pensados especialmente para você mandar bem na sua prova.
Nessa página estaremos interessados nas variações de fluxo magnético que está totalmente relacionado com a Lei de Faraday:
Lei de Faraday
Como podemos nos lembrar, a lei de Faraday define que uma variação no fluxo do campo magnético sobre um circuito produz uma força eletromotriz que pode gerar uma corrente no circuito.
Um bom exemplo são as lanternas a dínamo, não sei se você já viu uma dessas:

Ta vendo aquela parte lateral cinza ali dela, aquilo funciona como uma alavanca que movimenta um imã dentro da lanterna. Conforme esse imã se movimenta o fluxo do campo magnético varia o que gera uma força eletromotriz no circuito da lanterna e com a força eletromotriz surge uma corrente que acende e recarrega a lanterna.
Show... Vamos ver isso conceitualmente então, preparem-se!! Rsrs
Para encontrar o fluxo, usaríamos a seguinte expressão:
Podemos perceber que o fluxo é calculado a partir de um produto escalar entre dois vetores, lembrando de produto escalar podemos escrever:
Então para alterarmos o fluxo, ou variamos o módulo do campo, ou variamos a área do circuito, ou variamos o ângulo
Na lanterninha de exemplo ali em cima, o que você acha que está acontecendo? A área do circuito é sempre a mesma, o módulo do campo magnético é sempre o mesmo (ele só mudaria caso mudássemos a potência do imã).
Portanto o que estamos fazendo ao acionar a alavanca da lanterna é girar o imã interno o que provoca uma variação na orientação dos vetores, o que altera o ângulo
No nosso site você encontra as formas mais comuns em que isso aparece em provas como em espiras de área fixa e campo magnético variável, ou espiras de área variável com campo magnético fixo, ou espiras próximas a um fio.
Mas para você não ficar perdido, da uma olhada em um dos nossos exercícios com resolução Passo a Passo.
Exercício
Nesse vídeo você confere uma resolução de um exercício do nosso tópico de Variações do Fluxo Magnético, onde temos uma espira com área fixa e campo variável:
Uma espira de
A escala do eixo vertical é definida por
O plano da espira é perpendicular a
a)
b)
c)
Exercício
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 293-2
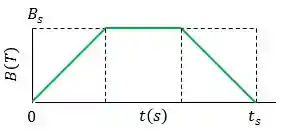
Uma espira de de raio e uma resistência de é submetida a um campo magnético uniforme cujo módulo varia de acordo com a figura abaixo.
A escala do eixo vertical é definida por , e a escala do eixo horizontal é definida por .
O plano da espira é perpendicular a . Determine a força eletromotriz induzida na espira durante os intervalos de tempo:
;
;
;
Passo 1
A espira tem área fixa e o seu plano é perpendicular ao campo magnético . Nesse caso, a induzida será dada por:
Onde:
Além disso, nesse gráfico, podemos ver que em alguns trechos, o campo magnético varia linearmente. Dessa forma, podemos dizer que:
Logo:
Beleza, agora só temos que aplicar isso em cada caso.
Passo 2
;
Aplicando a relação acima a esse caso, teremos:
Passo 3
;
Nesse intervalo, o campo magnético é constante, logo:
Passo 4
;
Resposta
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 293-6
Um campo magnético uniforme é perpendicular ao plano de uma espira circular com de diâmetro, formada por um fio com de diâmetro e uma resistividade de .
Qual deve ser a taxa de variação de para que uma corrente de seja induzida na espira?
Passo 1
Vamos começar calculando a induzida na espira. Como a área é constante e o campo magnético perpendicular ao plano da espira, a é dada por:
Onde:
Logo:
Passo 2
Através da Lei de Ohm, temos que:
Tá legal que o problema não nos deu exatamente a resistência, mas podemos calculá-la pela expressão:
Onde:
Jogando isso na expressão da resistência, teremos:
Assim, a induzida será:
Onde:
Logo:
Passo 3
Jogando o valor da induzida na expressão que encontramos no Passo 1, teremos:
Organizando um pouco a bagunça, teremos:
Onde:
Substituindo o valor, teremos:
Finalmente:
Resposta
Exercício Resolvido #3
UNICAMP – Prova 3 – 2012.1 – Manhã – Questão 2
Uma espira retangular tem comprimento , largura e resistência .
Suponha que numa região do espaço exista um campo magnético que cresce linearmente com , isto é, aumenta à medida que se afasta de a partir da origem, e é dado por , onde é uma constante. Este campo magnético está na direção de (”entrando no plano da página”).
A espira é então imersa nessa região, como mostra a figura abaixo, onde é a distância do centro da espira até o eixo .
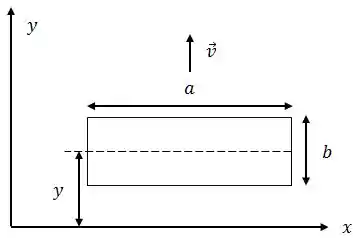
Determine:
- O fluxo do campo magnético através da espira.
- A corrente induzida na espira à medida que esta se afasta do eixo com velocidade constante ao longo de .
Passo 1
- O fluxo do campo magnético através da espira.
- A corrente induzida na espira à medida que esta se afasta do eixo com velocidade constante ao longo de .
Por definição, o fluxo magnético é dado por:
Podemos dizer que . Onde vai variar de até
Substituindo a expressão pro campo magnético que o problema nos deu:
Passo 2
Vamos lá... para encontrar a corrente induzida, precisamos calcular primeiro a fem induzida, para que possamos utilizar a fórmula:
Para calcular a fem induzida, podemos usar a lei de Faraday:
Conforme a espira se afasta do eixo , o valor de varia. Já que a velocidade é constante, podemos dizer que:
Então podemos reescrever o fluxo do campo magnético como:
A fem induzida, por sua vez, será, em módulo:
Agora sim podemos encontrar uma expressão para a corrente induzida:
Resposta
a.
b.
Exercício Resolvido #4
UFRJ – Prova 2 – 2013.1 – Questão Discursiva nº2 – letras a,b – Modificada.
Um bastão retilíneo, de comprimento , massa e resistência , desliza, sem atrito, sobre um fio (rígido) condutor ideal (sem resistência), em forma de . O sistema todo está completamente imerso em uma região de campo magnético constante (estacionário e uniforme), perpendicular ao plano que contém o sistema. Inicialmente, uma força externa é aplicada e o bastão move-se com uma velocidade constante para a direita. A partir do instante , essa força externa deixa de agir e o bastão passa a mover-se apenas sob a ação da força magnética, com velocidade . Despreza a capacitância e a autoindutância do sistema, assim como a corrente de deslocamento.
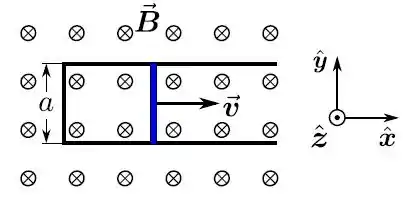
- Qual é o módulo da força eletromotriz induzida no circuito (fio + bastão)?
- Qual é o módulo da (intensidade de) corrente elétrica que passa pelo bastão?
Passo 1
A força eletromotriz pode ser calculada pela Lei de Faraday:
Precisamos calcular a taxa de variação do fluxo magnético. O fluxo é dado pela fórmula:
O campo pode ser escrito, de acordo com o enunciado, pela expressão:
Onde é uma constante positiva. Arbitremos nossa área no sentido positivo de . Portanto, o produto escalar fica:
Substituindo da fórmula, puxamos a constante para fora:
Que resulta na área do retângulo de dimensões:
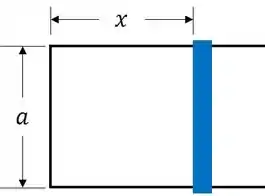
Portanto, o fluxo é:
Onde é uma função do tempo, pois a barra se move.
Passo 2
Substituindo na Lei de Faraday:
Puxando as constantes pra fora derivamos com respeito ao tempo:
Que é a conhecida expressão do módulo da velocidade:
Passo 3
Em seguida, gostaríamos de calcular a intensidade da corrente. Como sabemos que o circuito tem resistência , pela Lei de Ohm:
Logo:
Resposta
a)
b)
Exercício Resolvido #5
PUCRIO – Prova 3 – 2014.1 – Questão nº1
Uma barra condutora de comprimento é apoiada sobre trilhos condutores fixos e indeformáveis, definindo um circuito retangular, mostrado na figura. A resistência equivalente do circuito é constante e vale . Parte da superfície deste circuito é penetrada perpendicularmente por um campo magnético constante e uniforme de módulo , entrando na página.
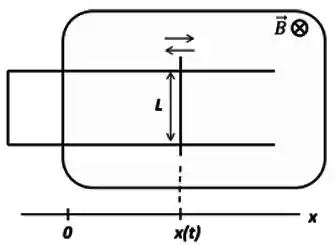
Por um mecanismo não mostrado na figura, a barra é forçada a oscilar, de modo que sua posição descreve um MHS (movimento harmônico simples), com equação dada por:
Calcule a fem induzida no circuito como uma função do tempo, .
Calcule o valor máximo da corrente induzida, .
Em uma nova situação, a barra é deixada em repouso na posição e o campo magnético, sem mudar sua orientação, varia no tempo de acordo com a função:
Encontre o valor máximo da corrente induzida.
Passo 1
Para determinar a fem induzida, vamos utilizar a Lei de Faraday, ela dos diz:
Vamos primeiro calcular o fluxo , se liga!
Arbitrando o vetor área no mesmo sentido do campo magnético, temos:
Sendo a área , substituindo o fluxo na equação da Lei de Faraday, temos:
Sabemos como varia em função de , pela equação que foi dada no enunciado:
Calculando a derivada, temos:
Substituindo na Lei de Faraday:
Vamos agora substituir os valores do campo e do comprimento da barra!
De onde surgiu aquele na fórmula acima?
Bom, o campo é dado em Tesla, ou seja, , no entanto, estamos utilizando a unidade centímetros e não metros. Por isso devemos dividir por , para que a unidade do campo vire ! Show??
Passo 2
Vamos determinar a corrente em função do tempo. Temos a nossa velha e conhecida fórmula:
Substituindo a função da fem, temos;
A corrente máxima ocorre quando , portanto:
Passo 3
Para resolver esse item, vamos fazer o mesmo mimimi que fizemos no item só que agora, temos como valor fixo e quem varia é o campo .
Vamos começar com a Lei de Faraday:
Vamos primeiro calcular o fluxo , se liga!
Arbitrando o vetor área no mesmo sentido do campo magnético, temos:
Sendo a área , substituindo o fluxo na equação da Lei de Faraday, temos:
Vamos agora calcular a derivada do campo magnético, se liga:
Substituindo na equação da tensão, e substituindo os valores de e , temos:
Veja que dessa vez estamos passando tudo para metro, pois o campo está em Tesla !
A corrente é dada por:
A corrente máxima ocorre quando , ou seja:
Resposta
.
.
.
Exercício Resolvido #6
UFRJ – Prova 2 – 2013.1 – Múltipla Escolha nº1.
Por um fio retilíneo, muito longo, em repouso, passa uma corrente elétrica estacionária de intensidade . Próximo a tal fio, há um retângulo condutor, rígido, coplanar com o fio, conforme mostra a figura. Originalmente, o retângulo também encontra-se em repouso, mas, em um certo instante, ele passa a se movimentar em uma das quatro maneiras seguintes: (1) translação com velocidade ; (2) Translação com velocidade ; (3) translação com velocidade , ou (4) rotação (rígida) em torno do eixo do próprio fio, com velocidade angular . Em qual(is) das quatro situações, não surge uma corrente elétrica induzida ao longo do retângulo?
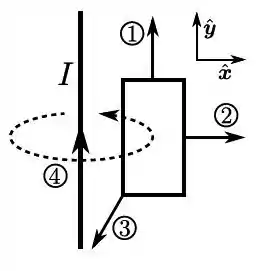
- Somente em 1
- Somente em 4
- Somente em 2
- Somente em 3
- Em 1 e 4
- Em 2 e 3
- Em nenhuma surgirá corrente induzida, pois o campo gerado pelo fio, mantém-se estacionária e a área do retângulo não varia
Passo 1
Enunciando a Lei de Faraday:
Juntando com a Lei de Ohm:
Portanto precisamos determinar em quais situações o fluxo magnético varia pelo circuito.
Passo 2
Na situação , o fluxo vai ser constante, pois a distância da espira ao fio não varia. Dessa forma:
Passo 3
Analogamente, na situação , o fluxo vai estar diminuindo:
Passo 4
Na situação , temos que uma das componentes da velocidade é em . Assim, haverá variação de fluxo, de forma que:
Passo 5
Na situação , também temos que a distância do fio não varia. Logo:
Resposta
Letra e
Exercício Resolvido #7
UNICAMP – Prova 3 – 2011.2 - Noturno – Questão nº2.
Na figura abaixo dois trilhos condutores retilíneos formam um ângulo reto. Uma barra condutora em contato com os trilhos parte do vértice no instante , com uma velocidade constante .
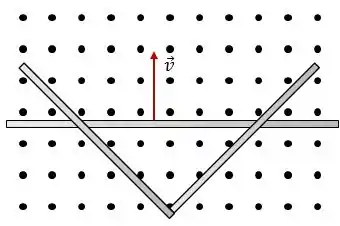
Há um campo magnético dirigido para fora da página, em toda a região. Determine:
- O fluxo magnético em função do tempo ;
- A induzida aplicada ao triângulo em função do tempo;
- Se a , onde e são constantes, e sabendo o valor de para , determine o valor de .
Passo 1
- O fluxo magnético em função do tempo ;
- A induzida aplicada ao triângulo em função do tempo;
- Se a , onde e são constantes, e sabendo o valor de para , determine o valor de .
Por definição, o fluxo magnético é dado por:
Como o campo magnético é constante:
Onde é a área do triângulo.
A área de um triângulo é dada por:
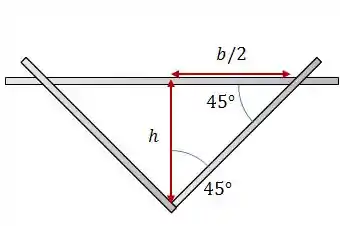
Analisando a geometria do problema, podemos ver que . Logo:
Como a barra horizontal se desloca com velocidade constante , podemos relacionar a velocidade com a altura da barra por:
Portanto, o fluxo magnético será dado por:
Passo 2
De acordo com a lei de Faraday, a induzida é dada por:
Agora ficou fácil, é só derivar o cara que achamos no passo 1.
Passo 3
Eu sei que essa agora pode parecer viagem, mas o negócio aqui é só comparar com a expressão da que já tínhamos encontrado.
Para que os dois lados sejam iguais:
Acabou!
Resposta
a.
b.
c.
Exercício Resolvido #8
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 297-34.
Na figura abaixo uma espira retangular muito longa, de largura , resistência e massa , está inicialmente suspensa na presença de um campo magnético horizontal uniforme orientado para dentro do papel, que existe apenas acima da reta .
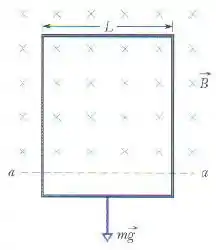
Deixa-se cair a espira, que acelera sob a ação da gravidade até atingir uma certa velocidade terminal . Escreva uma expressão para , ignorando a resistência do ar.
Passo 1
Quando a espira atinge a velocidade terminal , a velocidade passa a ser constante e a força resultante sobre a espira é nula.
Para que isso seja verdade, é necessário que a força magnética sobre a espira seja igual ao peso da mesma, certo?
Logo:
Assim, a corrente induzida na espira será:
Beleza, agora precisamos nos resolver com essa corrente.
Passo 2
A corrente induzida na espira será dada por:
Para esse tipo de problema, sabemos que a induzida será dada por:
Portanto:
Passo 3
Igualando as expressões dos passos 1 e 2, teremos:
Organizando esses caras, teremos:
Resposta
Exercício Resolvido #9
UFRJ – Prova Final – 2014.1 – Questão Discursiva nº2.
A figura mostra uma barra retilínea condutora, de massa , comprimento e resistência elétrica , movendo-se com uma velocidade constante ao longo de trilhos condutores, retilíneos horizontais, fixos.
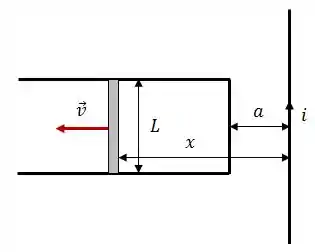
Tal circuito está sob ação de um campo magnético gerado por uma corrente elétrica estacionária fluindo por um fio retilíneo longo, paralelo à barra e no mesmo plano do circuito.
A resistência dos trilhos, assim como a capacitância e a autoindutância do circuito e a indutância mútua entre o circuito e o fio retilíneo (de corrente ) podem e devem ser desprezadas.
Obtenha uma expressão para a corrente elétrica no circuito, , como função da distância da barra ao fio.
[Sugestão: não precisa deduzir o campo magnético de uma corrente retilínea estacionária, muito longa.]
Obtenha uma expressão para a taxa temporal de dissipação de energia, pelo efeito Joule, na barra, como função de .
Obtenha uma expressão para a força externa que precisa ser aplicada à barra para manter a sua velocidade constante.
Passo 1
Obtenha uma expressão para a corrente elétrica no circuito, , como função da distância da barra ao fio.
Vamos por partes... Para calcular a corrente elétrica no circuito, primeiro vamos ter que calcular a induzida , de forma que:
A induzida, de acordo com a lei de Faraday, é dada por:
Então vamos precisar calcular o fluxo magnético, definido por:
Mas antes, teremos que encontrar a expressão do campo magnético gerado pelo fio de corrente , que é calculado através da lei de Ampère, dada por:
Então, no fim, serão mais 4 passos... Viu o tamanho do drama?
Mas nós damos conta!
Passo 2
Por conta da simetria do problema, a amperiana será uma circunferência de raio , logo:
Pela regra da mão direita, na região da espira, o campo magnético está saindo do plano da página.
Passo 3
O elemento de área será dado por:
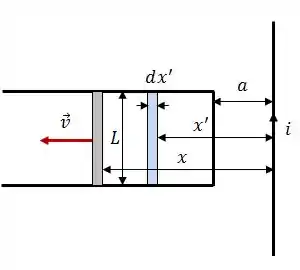
Portanto:
Passo 4
Pela Lei de Faraday:
Passo 5
A corrente será dada por:
Passo 6
Obtenha uma expressão para a taxa temporal de dissipação de energia, pelo efeito Joule, na barra, como função de .
A “taxa de dissipação de energia” é a mesma coisa que “potência dissipada”, que é dada por:
Logo:
Passo 7
Obtenha uma expressão para a força externa que precisa ser aplicada à barra para manter a sua velocidade constante.
Para manter a barra com velocidade constante, a força externa deve ter a mesma direção da força magnética sobre a barra, o mesmo sentido, porém sentidos opostos, de forma que:
A força magnética sobre a barra é dada por:
Logo:
Substituindo o a expressão de , teremos:
Portanto:
Resposta
Exercício Resolvido #10
UFRJ – Prova Final – 2014.2 – Múltipla Escolha nº7.
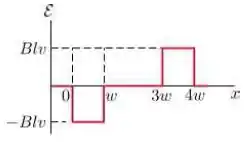
Uma espira condutora retangular de dimensões e se move com velocidade constante para a direita, conforme a figura.
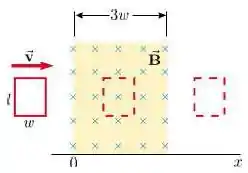
A espira atravessa um campo magnético uniforme e estacionário , dirigido para dentro da página, numa extensão de ao longo do eixo .
Assinale abaixo o gráfico que melhor representa a forca eletromotriz como função da posição da lateral à direita da espira:
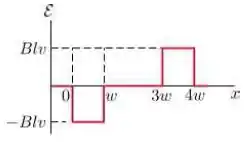
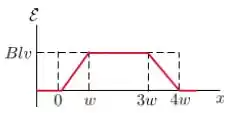
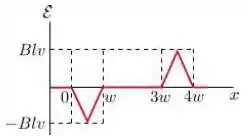
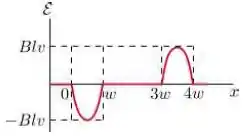
Passo 1
A induzida, de acordo com a lei de Faraday, é dada por:
Então a induzida depende da variação do fluxo magnético.
Assim, nas regiões , e não há variação do fluxo magnético porque, ou a espira está fora da região com o campo magnético, ou totalmente imersa na região com o campo magnético.
Passo 2
Durante o processo de entrada e saída da espira da região com o campo magnético, a área por onde passa campo magnético através da espira é dada por:
Visto que a área varia conforme a espira entra na região.
Assim, a induzida será dada por:
Como, durante a entrada, :
Ou seja, o valor é constante no processo de entrada e será também durante o processo de saída, mudando somente o sinal.
Portanto, a alternativa que melhor representa a induzida é a letra .
Resposta