Lei de Faraday
Teoria
A Lei de Faraday diz que a variação do Fluxo do Campo Magnético gera uma força eletromotriz induzida.
Se liga nessa imagem:
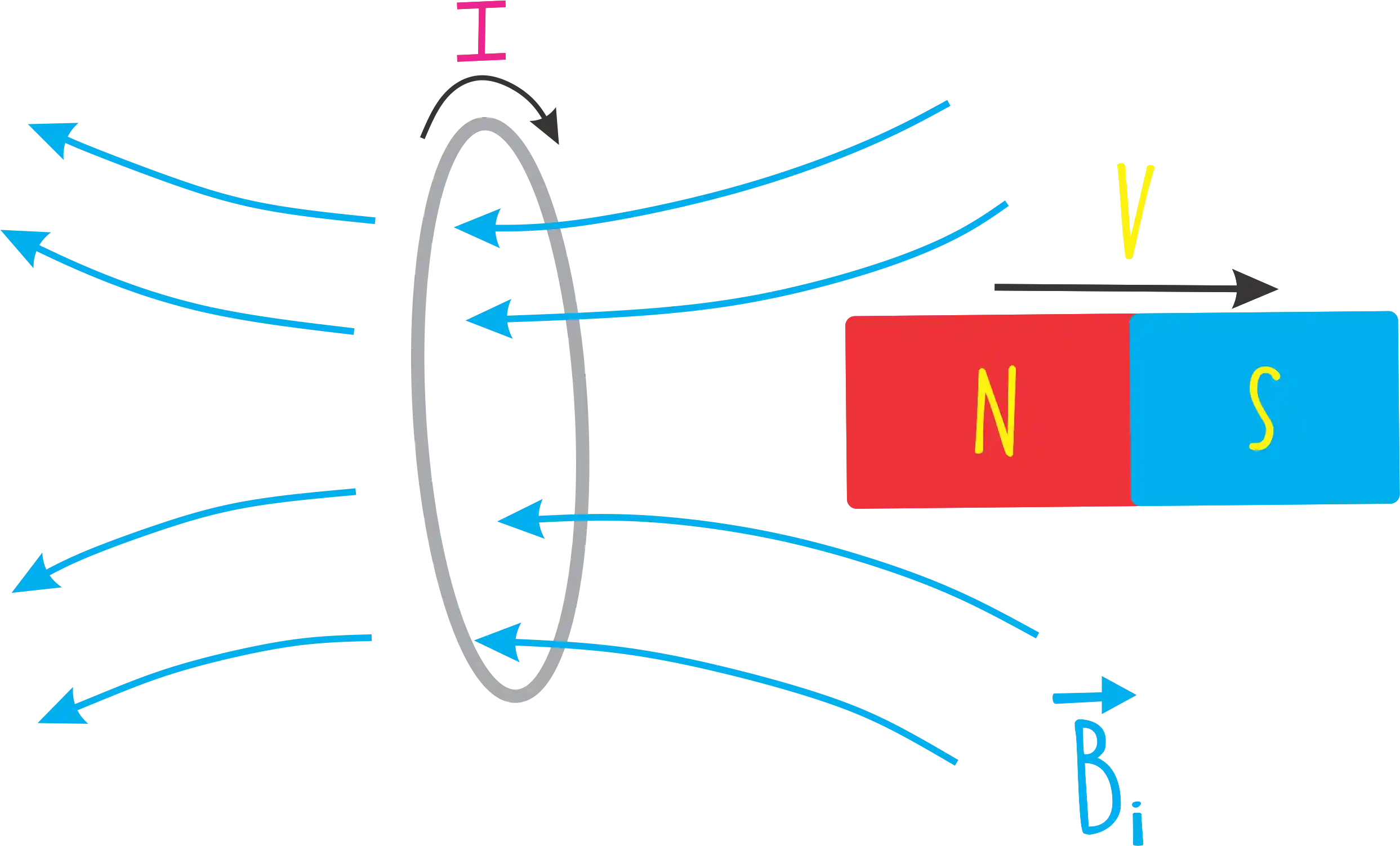
Por exemplo, se a gente aproxima um imã de uma espira, como mostrado na figura acima, estamos variando o fluxo do campo magnético e como resultado temos uma força eletromotriz induzida
Lei de Faraday - Fórmula
Sem mais delongas, matematicamente, escrevemos a lei de Faraday assim:
Onde:
é Força eletromotriz induzida (volts) ; é o Fluxo do campo magnético pela área do circuito.
-Beleza, mas como encontramos o fluxo?!
Excelente pergunta! Para encontrar o fluxo, usamos a seguinte fórmula:
O fluxo é calculado a partir de um produto escalar entre dois vetores. Na prática, podemos escrever o produto escalar da seguinte forma:
Então para alterarmos o fluxo, ou variamos o módulo do campo, ou variamos a área do circuito, ou variamos o ângulo
Lei de Lenz
A lei de Lenz completa a Lei de Faraday! Enquanto a Lei de Faraday nos da a magnitude da força eletromotriz produzida, a Lei de Lenz nos diz a direção do fluxo da corrente.
A Lei de Lenz diz que “O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito”.
Se liga nesse esquema:
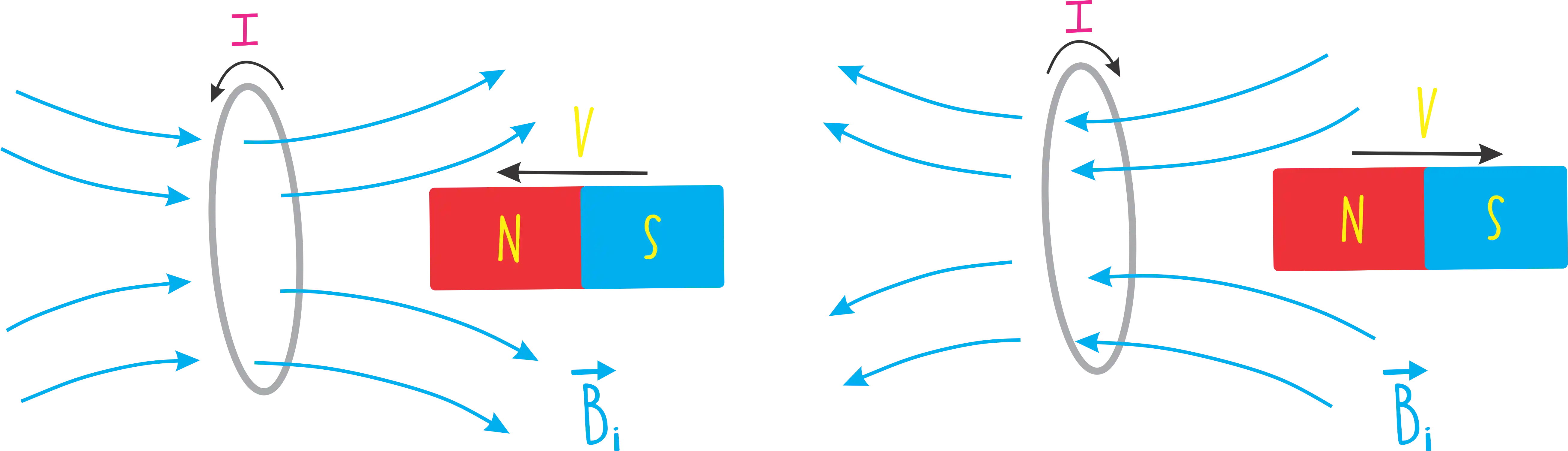
Como a gente viu lá em cima, se a gente aproxima um imã de uma espira estamos variando o fluxo do campo magnético
Segundo a Lei de Lenz vai ocorrer um efeito que vai se opor a essa variação de fluxo magnético criado. Ou seja, vai ser criado um campo magnético induzido
Vídeo Aula - Variação do Fluxo Magnético
Quer entender mais sobre como funciona essa tal de variação do fluxo magnético tão importante na Lei de Faraday?!
Então se liga nesse vídeozinho abaixo 👇
Agora vamos praticar com exercícios?!
Lei de Faraday - Fórmula
Lei de Lenz
Vídeo Aula - Variação do Fluxo Magnético
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ – Prova 2 – 2012.1 – Múltipla Escolha nº6.
Considere três anéis circulares muito finos: (I) um condutor; (II) um isolante, e (III) um com metade condutora e metade isolante. Eles são colocados, em repouso, separadamente, numa região de campo magnético não estacionário, uniforme, perpendicular ao plano do anel. Em que casos surge uma força eletromotriz ao longo do anel?
- I
- II
- III
- I e II
- I e III
- II e III
- I, II e III
- Nenhum deles
Passo 1
Pela Lei de Faraday:
Ou seja, surge uma fem num circuito onde há variação do fluxo magnético. Ela não diz respeito ao material do circuito.
Passo 2
Como os anéis estão numa região de campo magnético não estacionário, existe variação do fluxo magnético. Por conta disso, deve haver fem induzida em todos os três anéis.
Resposta
Letra g
Exercício Resolvido #2
UFRJ – Prova 2 – 2014.2 – Múltipla Escolha nº6.
Considere dois anéis circulares, um condutor e outro isolante, pertencentes a um mesmo plano, sujeitos a um campo magnético variável no tempo, perpendicular ao plano dos anéis.
Estando os dois anéis em repouso, em qual deles surgirá uma força eletromotriz induzida? Em qual deles surgirá uma corrente induzida?
Em nenhum dos anéis. Em nenhum dos anéis.
Em nenhum dos anéis. Somente no anel condutor.
Somente no anel condutor. Somente no anel condutor.
Em ambos os anéis. Somente no anel condutor.
Em ambos os anéis. Em ambos os anéis.
Passo 1
De acordo com a lei de Faraday, a induzida é dada por:
Como o fluxo de campo magnético não depende do material a força eletromotriz induzida surgira em ambos os anéis.
Passo 2
Já a corrente induzida é dada por:
Ou seja, esse cara depende do material.
Em um material isolante:
Ou seja, não surgirá corrente no anel isolante.
Em um material condutor a resistência não é tão grande, assim .
Ou seja, surgirá corrente induzida somente no anel condutor.
A resposta certa é a letra .
Resposta
Em ambos os anéis. Somente no anel condutor.
Exercício Resolvido #3
UFRJ – Prova 2 – 2015.1 – Múltipla Escolha nº8
Seja uma superfície esférica dividida em duas semiesferas e por uma espira circular condutora ôhmica .
Sabendo-se a esfera está numa região onde há um campo magnético , que a espira tem uma resistência finita e desprezando qualquer efeito auto indutivo ou capacitivo, podemos afirmar que
o fluxo de através de é nulo.
o fluxo de através de é proporcional à corrente induzida na espira .
a circulação de em torno de é proporcional à corrente através de .
a taxa de variação temporal do fluxo de através de é proporcional à corrente induzida na espira .
a taxa de variação temporal do fluxo de através de é nula.
Passo 1
Vamos analisar cada opção, ok?
o fluxo de através de é nulo.
O fluxo magnético através de é dado por:
O fluxo magnético só vai ser nulo se e forem perpendiculares. Como não há nada no problema que indique isso, a afirmação é falsa.
Passo 2
o fluxo de através de é proporcional à corrente induzida na espira .
Na verdade, a corrente induzida é proporcional à induzida, que é proporcional à taxa de variação do fluxo magnético. Logo:
A afirmação é falsa.
Passo 3
a circulação de em torno de é proporcional à corrente através de .
A circulação de através de é dada pela lei de Ampère:
Mas ela seria válida se houvesse alguma corrente através de , logo, a afirmação é falsa.
Passo 4
a taxa de variação temporal do fluxo de através de é proporcional à corrente induzida na espira .
Opa! Essa já matamos lá em cima. Já havíamos concluído que:
A afirmação é verdadeira.
A resposta certa é a letra .
Passo 5
a taxa de variação temporal do fluxo de através de é nula.
Essa cai no mesmo caso da letra .
A afirmação é falsa.
Resposta
a taxa de variação temporal do fluxo de através de é proporcional à corrente induzida na espira .
Exercício Resolvido #4
UFRJ – Prova 2 – 2015.1 – Múltipla Escolha nº9.
Uma espira circular de área é atravessada por um campo magnético uniforme que oscila periodicamente no tempo. As dependências temporais dos campos (curva cheia) e (curva pontilhada) estão ilustradas nas figuras abaixo.
A máxima e o fluxo máximo de campo magnético se dão, respectivamente, nas situações
e .
e .
e .
e .
Para determinarmos a máxima e o fluxo máximo precisaríamos conhecer a resistência oferecida pelas espiras.
Passo 1
Analisando os gráficos, podemos notar algumas coisas.
A primeira delas é que as equações dos campos terão mais ou menos essa cara:
Onde e . Logo:
Além disso, podemos relacionar as frequências e através dos períodos dos gráficos.
Portanto:
Agora podemos trabalhar.
Passo 2
A induzida é proporcional à variação do fluxo magnético. Mas como a área é constante, a induzida será proporcional à variação do campo magnético.
Sendo assim:
Assim, .
Logo, o gráfico representa a máxima.
Passo 3
O fluxo magnético é proporcional ao campo magnético, logo:
Assim, .
Logo, o gráfico representa o fluxo magnético máximo.
A resposta certa é a letra .
Resposta
e .
Exercício Resolvido #5
UFRJ – Prova 2 – 2013.1 – Múltipla Escolha nº7.
Em uma certa região, temos um campo magnético uniforme. Qual é o módulo do seu fluxo através da superfície sombreada, constituída pela superfície lateral de um cilindro circular inclinado e uma de suas bases, perpendicular ao campo?
Passo 1
O jeito com o qual vamos resolver essa questão é um pouco diferente. Trata-se de um caso clássico da Lei de Gauss para o magnetismo (talvez seja legal você rever Lei de Gauss, se tiver dúvidas..).
Parece bastante desagradável fazer essa integral para toda a maldita superfície:
Então vamos fechar ela com a tampa que está aberta:
Respeitando a orientação.
Passo 2
Sabemos que, pela Lei de Gauss para o magnetismo, o fluxo magnético por uma superfície fechada é sempre zero, logo:
Então calculamos o fluxo pela tampa, que é simples pois o vetor área é paralelo ao campo:
Passo 3
Então:
Como o sinal não importava pra começo de conversa... Ignored. O módulo do fluxo que ele queria é esse aí:
Resposta
Letra a
Exercício Resolvido #6
Site do Prof. A. F. Guimarães, lista 09 de Física 3
Numa região do espaço existe um campo magnético tal que é um vetor constante no espaço, porém variável no tempo. Coloca-se neste campo uma espira contida num plano que forma um ângulo com o vetor . A área da espira é , sendo que o valor de pode variar com o tempo. Suponha que a espira esteja girando no campo, de modo que o ângulo possa variar com o tempo. Encontre uma expressão da força eletromotriz induzida na espira.
Passo 1
O fluxo do vetor indução magnética é dado por:
A força eletromotriz será dada por:
Passo 2
Substituindo uma equação na outra, teremos que:
Resposta
Exercício Resolvido #7
UFRJ, Física 3, P2 – 2011.2 Questão ME08
Uma espira circular condutora em repouso está em uma região onde existe um campo magnético uniforme, dependente do tempo , cuja direção coincide com a do eixo perpendicular ao plano da espira. A função é dada pela figura. Marque a opção que melhor representa a força eletromotriz induzida na espira.
Passo 1
Primeiramente, vamos lembrar o que diz a lei de Faraday:
“uma variação no fluxo do campo magnético pela área do circuito produz uma força eletromotriz nele”
Temos um campo magnético variando? SIM. O enunciado diz “campo magnético uniforme, dependente do tempo”! Se ele depende do tempo, ele varia! Não se confundao com a palavra “uniforme”, lembra que em física 1 nós tínhamos movimento uniformemente variado? Não esquece disso!
A fórmula da lei de Faraday é a seguinte:
Esta fórmula nada mais é do que uma derivada, a derivada do fluxo do campo magnético com o tempo é igual à força eletromotriz induzida, mas com sinal oposto.
A figura dada, mostra exatamente a variação do fluxo de campo magnético com o tempo.
Passo 2
Agora vamos avaliar a figura:
No intervalo de tempo :
Temos uma variação negativa. O gráfico tem o formato parabólico, o que representa uma função do segundo grau. A derivada de uma função do segundo grau é uma função do primeiro grau, ou seja, uma reta!
Entao a nossa força eletromotriz induzida neste intervalo deverá aparecer no gráfico como uma reta. Além disso, como temos uma variação negativa, a nossa força eletromotriz terá o sinal contrário à essa variação, portanto ela será positiva!
Passo 3
No intervalo de tempo :
Neste intervalo, não há variação no fluxo do campo magnético, portanto a força eletromotriz induzida é nula.
Passo 4
No intervalo de tempo :
Neste intervalo, a variação no fluxo do campo magnético é negativa.O gráfico tem o formato de uma reta, ou seja, uma função do primeiro grau. A derivada de uma função do primeiro grau é uma função de grau zero, ou seja, uma constante.
Entao a nossa força eletromotriz induzida neste intervalo deverá aparecer no gráfico como uma constante. Além disso, como temos uma variação negativa, a nossa força eletromotriz terá o sinal contrário à essa variação, portanto ela será positiva!
Passo 5
No intervalo de tempo :
Neste intervalo, a variação no fluxo do campo magnético é positiva.O gráfico tem o formato de uma reta, ou seja, uma função do primeiro grau. A derivada de uma função do primeiro grau é uma função de grau zero, ou seja, uma constante.
Entao a nossa força eletromotriz induzida neste intervalo deverá aparecer no gráfico como uma constante. Além disso, como temos uma variação positiva, a nossa força eletromotriz terá o sinal contrário à essa variação, portanto ela será negativa!
Passo 6
Juntando tudo que vimos nos passos anteriores, a única opção possível é a letra (a)
Resposta
Exercício Resolvido #8
UFRJ, Física 3, P2 – 2012.2 Questão ME01
Considere dois anéis circulares em repouso: um condutor (1) e outro isolante (2). Ambos estão sujeitos a campos magnéticos não estacionários orientados para dentro do plano dos anéis. Quanto ao campo elétrico induzido e à corrente elétrica induzida I, nos anéis, podemos afirmar que:
(a) [1] = , I[1] = 0; [2] = , I[2] = 0 .
(b) [1] , I[1] 0; [2] = , I[2] = 0 .
(c) [1] , I[1] 0; [2] , I[2] = 0 .
(d) [1] I[1] 0; [2] , I[2] 0 .
(e) [1] = , I[1] 0; [2] = , I[2] = 0 .
Passo 1
Bom, primeiramente, o que diz a lei de Faraday?
“uma variação no fluxo do campo magnético pela área do circuito produz uma força eletromotriz nele”
Temos um campo magnético variando? SIM. O enunciado diz “campos magnéticos não estacionários”!
Portanto vai haver uma força eletromotriz em ambos os anéis, já que a lei de Faraday não fala nada sobre o tipo de material (condutor ou isolante).
Ué, mas se temos uma força eletromotriz, temos uma diferença de potencial e se temos uma diferença de potencial temos um campo elétrico.
Portanto, temos que:
Passo 2
Quanto à corrente elétrica, sabemos que só vai haver movimentação de cargas (corrente elétrica) se o material for condutor.
Portanto, haverá corrente no anel 1 e não haverá corrente no anel 2.
Passo 3
Juntando tudo:
A alternativa correta é a letra (c).
Resposta
(c) [1] , I[1] 0; [2] , I[2] = 0 .