Exercícios de Variações do Fluxo Magnético - Lista de Exercícios Resolvida
Questão 1
Um campo magnético uniforme é perpendicular ao plano de uma espira circular com de diâmetro, formada por um fio com de diâmetro e uma resistividade de .
Qual deve ser a taxa de variação de para que uma corrente de seja induzida na espira?
Ver solução completaQuestão 2
Na figura abaixo uma espira retangular muito longa, de largura , resistência e massa , está inicialmente suspensa na presença de um campo magnético horizontal uniforme orientado para dentro do papel, que existe apenas acima da reta .
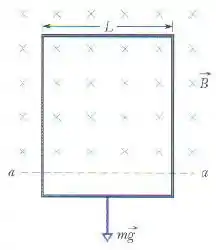
Deixa-se cair a espira, que acelera sob a ação da gravidade até atingir uma certa velocidade terminal . Escreva uma expressão para , ignorando a resistência do ar.
Ver solução completaQuestão 3
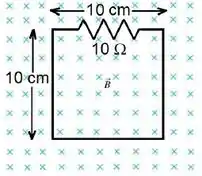
Uma barra condutora de comprimento é apoiada sobre trilhos condutores fixos e indeformáveis, definindo um circuito retangular, mostrado na figura. A resistência equivalente do circuito é constante e vale . Parte da superfície deste circuito é penetrada perpendicularmente por um campo magnético constante e uniforme de módulo , entrando na página.
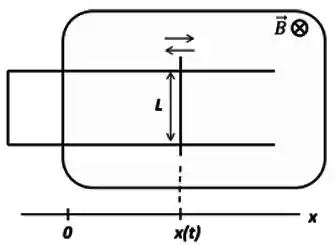
Por um mecanismo não mostrado na figura, a barra é forçada a oscilar, de modo que sua posição descreve um MHS (movimento harmônico simples), com equação dada por:
Calcule a fem induzida no circuito como uma função do tempo, .
Calcule o valor máximo da corrente induzida, .
Em uma nova situação, a barra é deixada em repouso na posição e o campo magnético, sem mudar sua orientação, varia no tempo de acordo com a função:
Encontre o valor máximo da corrente induzida.
Ver solução completaQuestão 4
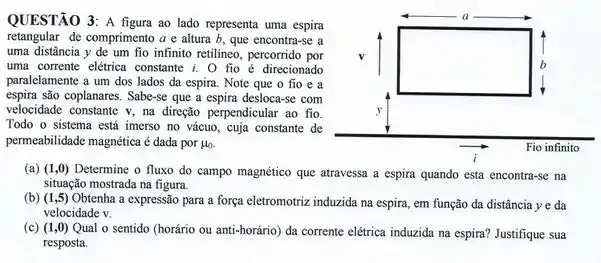
A figura mostra uma barra retilínea condutora, de massa , comprimento e resistência elétrica , movendo-se com uma velocidade constante ao longo de trilhos condutores, retilíneos horizontais, fixos.
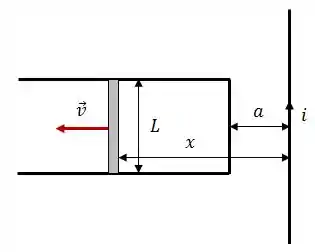
Tal circuito está sob ação de um campo magnético gerado por uma corrente elétrica estacionária fluindo por um fio retilíneo longo, paralelo à barra e no mesmo plano do circuito.
A resistência dos trilhos, assim como a capacitância e a autoindutância do circuito e a indutância mútua entre o circuito e o fio retilíneo (de corrente ) podem e devem ser desprezadas.
Obtenha uma expressão para a corrente elétrica no circuito, , como função da distância da barra ao fio.
[Sugestão: não precisa deduzir o campo magnético de uma corrente retilínea estacionária, muito longa.]
Obtenha uma expressão para a taxa temporal de dissipação de energia, pelo efeito Joule, na barra, como função de .
Obtenha uma expressão para a força externa que precisa ser aplicada à barra para manter a sua velocidade constante.
Ver solução completaQuestão 5
Uma espira retangular tem comprimento , largura e resistência .
Suponha que numa região do espaço exista um campo magnético que cresce linearmente com , isto é, aumenta à medida que se afasta de a partir da origem, e é dado por , onde é uma constante. Este campo magnético está na direção de (”entrando no plano da página”).
A espira é então imersa nessa região, como mostra a figura abaixo, onde é a distância do centro da espira até o eixo .
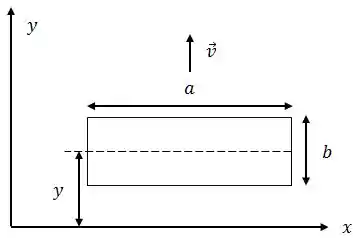
Determine:
- O fluxo do campo magnético através da espira.
- A corrente induzida na espira à medida que esta se afasta do eixo com velocidade constante ao longo de .
Questão 6
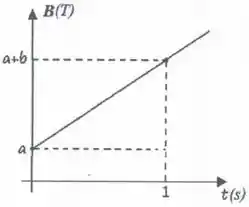
Uma espira de de raio e uma resistência de é submetida a um campo magnético uniforme cujo módulo varia de acordo com a figura abaixo.
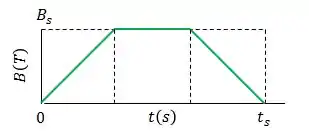
A escala do eixo vertical é definida por , e a escala do eixo horizontal é definida por .
O plano da espira é perpendicular a . Determine a força eletromotriz induzida na espira durante os intervalos de tempo:
;
;
;
Ver solução completaQuestão 7
Na figura abaixo dois trilhos condutores retilíneos formam um ângulo reto. Uma barra condutora em contato com os trilhos parte do vértice no instante , com uma velocidade constante .
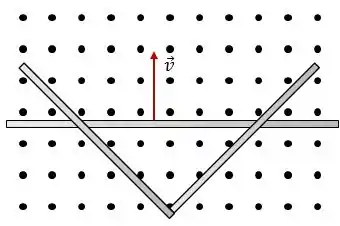
Há um campo magnético dirigido para fora da página, em toda a região. Determine:
- O fluxo magnético em função do tempo ;
- A induzida aplicada ao triângulo em função do tempo;
- Se a , onde e são constantes, e sabendo o valor de para , determine o valor de .
Questão 8
Por um fio retilíneo, muito longo, em repouso, passa uma corrente elétrica estacionária de intensidade . Próximo a tal fio, há um retângulo condutor, rígido, coplanar com o fio, conforme mostra a figura. Originalmente, o retângulo também encontra-se em repouso, mas, em um certo instante, ele passa a se movimentar em uma das quatro maneiras seguintes: (1) translação com velocidade ; (2) Translação com velocidade ; (3) translação com velocidade , ou (4) rotação (rígida) em torno do eixo do próprio fio, com velocidade angular . Em qual(is) das quatro situações, não surge uma corrente elétrica induzida ao longo do retângulo?
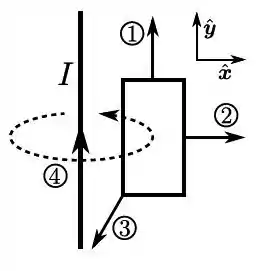
- Somente em 1
- Somente em 4
- Somente em 2
- Somente em 3
- Em 1 e 4
- Em 2 e 3
- Em nenhuma surgirá corrente induzida, pois o campo gerado pelo fio, mantém-se estacionária e a área do retângulo não varia
Questão 9
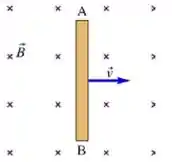
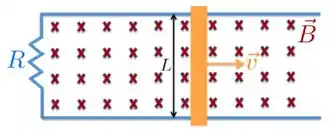
Uma espira condutora retangular de dimensões e se move com velocidade constante para a direita, conforme a figura.
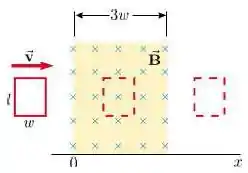
A espira atravessa um campo magnético uniforme e estacionário , dirigido para dentro da página, numa extensão de ao longo do eixo .
Assinale abaixo o gráfico que melhor representa a forca eletromotriz como função da posição da lateral à direita da espira:
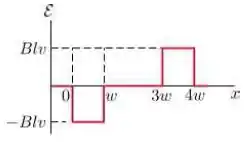
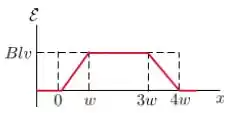
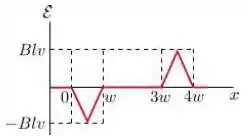
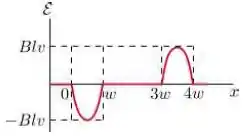
Questão 10
Um bastão retilíneo, de comprimento , massa e resistência , desliza, sem atrito, sobre um fio (rígido) condutor ideal (sem resistência), em forma de . O sistema todo está completamente imerso em uma região de campo magnético constante (estacionário e uniforme), perpendicular ao plano que contém o sistema. Inicialmente, uma força externa é aplicada e o bastão move-se com uma velocidade constante para a direita. A partir do instante , essa força externa deixa de agir e o bastão passa a mover-se apenas sob a ação da força magnética, com velocidade . Despreza a capacitância e a autoindutância do sistema, assim como a corrente de deslocamento.
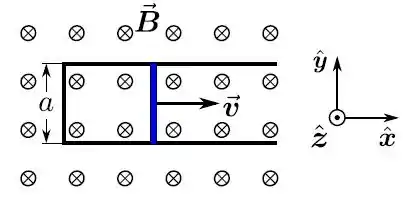
- Qual é o módulo da força eletromotriz induzida no circuito (fio + bastão)?
- Qual é o módulo da (intensidade de) corrente elétrica que passa pelo bastão?
Questão 12
A figura ao lado mostra uma barra de comprimento que se move com velocidade constante ao longo de trilhos paralelos ao eixo , conectados por um segmento contido no eixo . Os trilhos e o segmento são condutores, fixos e indeformáveis e o plano é horizontal. No eixo existe um fio muito comprido percorrido por uma corrente que cria um campo magnético não uniforme dado pela Lei de Ampère.
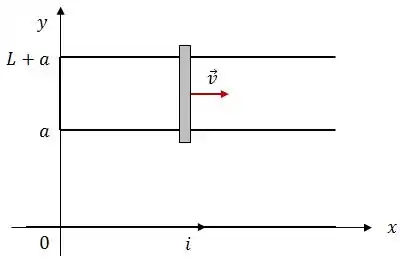
Encontre a força eletromotriz induzida na barra.
Supondo que a resistência da barra vale e as dos trilhos e do segmento são desprezíveis, calcule a corrente induzida e indique o seu sentido.
Calcule a força realizada por um agente externo para manter a barra se deslocando com velocidade constante. Indique o sentido da força externa.
Ver solução completaQuestão 13
A figura mostra uma barra de comprimento que é forçada a se mover com velocidade constante ao longo de trilhos horizontais.
Os trilhos são conectados à direita por um fio condutor. A barra, os trilhos e o fio formam assim uma espira condutora. A resistência elétrica da barra vale , a resistência do resto da espira é desprezível. Uma corrente que percorre um fio longo situado a uma distância a da espira produz um campo magnético (não uniforme) que atravessa a espira (como mostrado em figura).
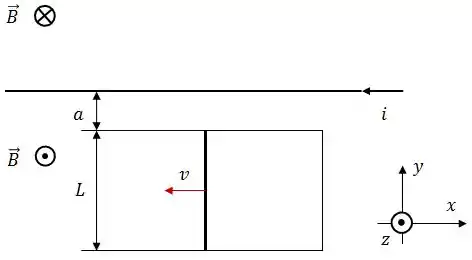
Nestas condições, determine:
a força eletromotriz induzida na espira;
a corrente induzida na espira;
a potência dissipada da espira;
o módulo, a direção e o sentido da força que deve ser aplicada à barra por um agente externo para que esta se mova com velocidade constante.
Ver solução completaQuestão 14
Uma barra condutora de resistência desprezível, comprimento e massa , está deslizando para baixo em movimento uniforme com velocidade , sob ação apenas de sua força peso e de uma força magnética. Esta força é gerada pelo campo magnético externo (uniforme e constante) aplicado na direção entrando na folha de papel, e de módulo . A barra faz contato com trilhos condutores de resistência também desprezível e o circuito é fechado pela resistência .
Considere e que o campo magnético externo é muito intenso. De modo que o campo magnético devido à corrente induzida no circuito pode ser desprezado.
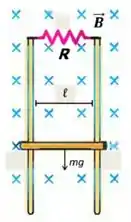
Responda, justificando, qual o sentido da corrente induzida no circuito (horário ou anti-horário) e qual o sentido do vetor força magnética sobre a barra (para cima ou para baixo).
Calcule o módulo da velocidade constante com que a barra desliza para baixo na montagem da figura.
Agora a barra foi fixada numa certa posição. A induzida no circuito como função do tempo é dada no gráfico abaixo. Faça um esboço qualitativo do gráfico do módulo do campo magnético externo em função do tempo. Faça a suposição de que começa em zero e é contínuo durante todo o intervalo, explicitando no eixo os instantes , , e .
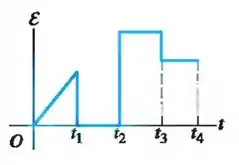
Questão 15
Uma barra condutora de comprimento é apoiada sobre trilhos condutores fixos e indeformáveis, definindo um circuito retangular, mostrado na figura. A resistência equivalente do circuito é constante e vale . Parte da superfície deste circuito é penetrada perpendicularmente por um campo magnético constante e uniforme de módulo , entrando na página.
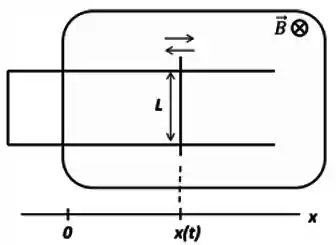
Por um mecanismo não mostrado na figura, a barra é forçada a oscilar, de modo que sua posição descreve um MHS (movimento harmônico simples), com equação dada por:
Calcule a fem induzida no circuito como um função do tempo, .
Calcule o valor máximo da corrente induzida, . Em seguida, para o primeiro período completo de oscilação da barra , encontre o(s) intervalo(s) de tempo em que a corrente induzida possui sentido horário e o(s) intervalo(s) em que ela possui sentido anti-horário.
Em uma nova situação, a barra é deixada em repouso na posição e o campo magnético, sem mudar sua orientação, varia no tempo de acordo com a função:
Encontre o valor máximo da corrente induzida e responda se seu sentido ‘horário ou anti-horário.
Ver solução completaQuestão 16
Um campo magnético uniforme atua apenas sobre uma região do espaço definida por um disco circular de raio e aponta para fora do plano do papel, como mostrado na figura abaixo. Duas partículas idênticas de carga , unidas por uma haste isolante rígida de comprimento , são posicionadas nesta região de forma que o eixo da haste é perpendicular à direção do campo e o centro dela coincide com o centro dessa região, como indicado. Sabendo que a haste encontra-se inicialmente em repouso e que a intensidade do campo magnético aumenta lentamente com o tempo, podemos afirmar que:
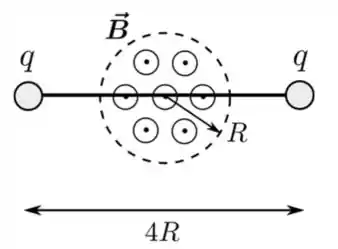
- A haste começará a girar em sentido anti-horário, devido ao torque gerado pela força elétrica.
- A haste começará a girar em sentido horário, devido ao torque gerado pela força magnética.
- A haste começará a girar em sentido anti-horário, devido ao torque gerado pela força magnética.
- A haste permanecerá em repouso, uma vez que a força resultante sobre ela é nula.
- A haste começará a girar em sentido horário, devido ao torque gerado pela força elétrica.
Questão 17
Por um fio retilíneo, muito longo, em repouso, passa uma corrente elétrica estacionária de intensidade . Próximo a tal fio, há um retângulo condutor, rígido, coplanar com o fio, conforme mostra a figura. Originalmente, o retângulo também encontra-se em repouso, mas, em um certo instante, ele passa a se movimentar em uma das quatro maneiras seguintes: (1) translação com velocidade ; (2) Translação com velocidade ; (3) translação com velocidade , ou (4) rotação (rígida) em torno do eixo do próprio fio, com velocidade angular . Em qual(is) das quatro situações, não surge uma corrente elétrica induzida ao longo do retângulo?
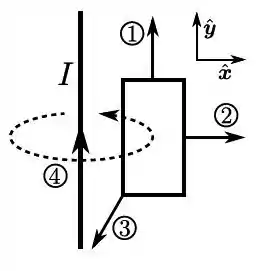
- Somente em 1
- Somente em 4
- Somente em 2
- Somente em 3
- Em 1 e 4
- Em 2 e 3
- Em nenhuma surgirá corrente induzida, pois o campo gerado pelo fio, mantém-se estacionária e a área do retângulo não varia
Questão 18
Um bastão retilíneo, de comprimento , massa e resistência , desliza, sem atrito, sobre um fio (rígido) condutor ideal (sem resistência), em forma de . O sistema todo está completamente imerso em uma região de campo magnético constante (estacionário e uniforme), perpendicular ao plano que contém o sistema. Inicialmente, uma força externa é aplicada e o bastão move-se com uma velocidade constante para a direita. A partir do instante , essa força externa deixa de agir e o bastão passa a mover-se apenas sob a ação da força magnética, com velocidade . Despreza a capacitância e a autoindutância do sistema, assim como a corrente de deslocamento.
- Qual é o módulo da força eletromotriz induzida no circuito (fio + bastão)?
- Qual é o módulo da (intensidade de) corrente elétrica que passa pelo bastão e o seu sentido?
- Qual é a força magnética (vetorial) sobre o bastão?
- Qual é a velocidade (vetorial) do bastão como função explícita do tempo, para ?
Questão 19
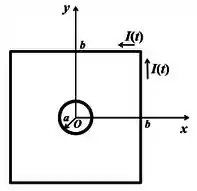
Uma espira condutora retangular , rígida, de comprimento e largura está sujeita a um campo magnético estacionário, mas não uniforme, perpendicular ao seu plano, tal que , onde são coordenadas cilíndricas, os correspondentes vetores unitários, conforme indicados na figura, e . O lado da espira, mais próximo ao eixo , está a uma distância desse. A espira constitui-se de um material ôhmico e sua resistência total é igual a , ao passo que a sua autoindutância é desprezível.
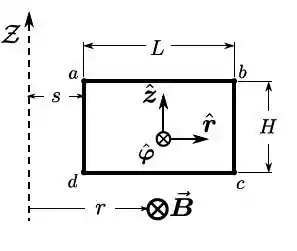
- Determine o módulo do fluxo do campo magnético que atravessa a região plana interior da espira.
- Determine, com justificativa detalhada, no caso de a espira estar em repouso, se alguma corrente induzida circula ao longo da espira e, se for o caso, indique claramente o seu sentido e calcule o seu módulo.
- Considere agora que a espira se desloca para a direita a uma velocidade de módulo constante . Nessa nova situação, determine novamente, com justificativa detalhada, se alguma corrente induzida circula ao longo da espira e, se for o caso, indique claramente o seu sentido e calcule o seu módulo.
Questão 20
O carrinho de plástico mostrado na figura abaixo se move sobre uma mesa horizontal sem atrito. Presa ao carrinho existe uma espira retangular condutora de lados e e resistência de . O plano da espira é paralelo ao plano da página. Um campo magnético uniforme de , dirigido perpendicularmente para dentro da página, existe na região a partir de , conforme mostrado. As massas do carrinho e da espira são desprezíveis. Quando a frente da espira está em , sua velocidade é de . Nesse instante, a intensidade da corrente induzida na espira é:
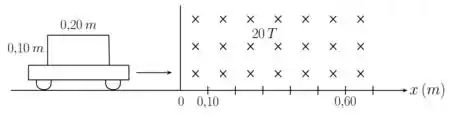
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 21
Um campo magnético uniforme passo pelo interior de uma região circular de raio e é perpendicular ao plano definido por essa região e sua intensidade aumenta a uma taxa constante . O gráfico que melhor representa o módulo do campo elétrico induzido para pontos internos e externos à região onde é diferente de zero vale:
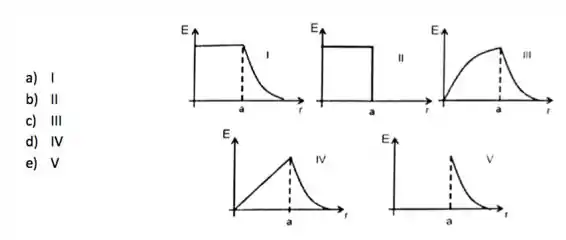
Questão 23
Uma barra condutora é movida com velocidade constante , sobre dois fios condutores separados por uma distância . A coordenada da barra no instante é .
Um resistor de resistência em está conectado às extremidades dos dois fios, formando o circuito fechado mostrado na figura. Um campo magnético uniforme e crescente com o tempo , onde , está presente na região. Nas perguntas abaixo considere o tempo apenas no intervalo .
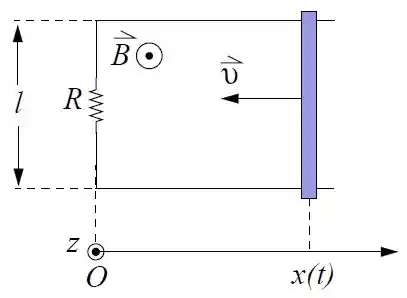
Determine a força eletromotriz induzida no circuito como função do tempo .
Calcule a corrente induzida no circuito e determine o instante de tempo no qual ela se anula.
Determine o sentido da corrente (horário ou anti-horário) como função do tempo .
Ver solução completaQuestão 24
Uma espira quadrada de lado e resistência está sobre uma mesa, a uma distância de um fio muito longo sobre o eixo que transporta uma corrente , conforme mostra a figura. O módulo do campo produzido pelo fio é , onde é a distância até o fio.
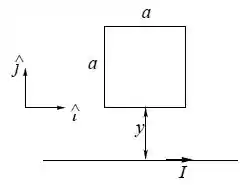
- Calcule o fluxo do campo magnético, produzido pelo fio através da espira.
- A espira é movimentada na direção , afastando-se do fio com velocidade . Use a lei de Lenz para determinar o sentido da corrente induzida na espira (horário ou anti-horário), justificando sua resposta. Calcule a corrente induzida .
- Determine o valor da corrente induzida se a espira é movimentada para a direita (direção ) mantendo constante a distância até o fio.
Questão 26
Uma bobina retangular de voltas e lados e está totalmente imersa numa região de campo magnético homogêneo de intensidade . Ela gira com relação a um eixo perpendicular ao campo magnético e perpendicular a um de seus lados com uma velocidade angular de , como mostra a figura. Os extremos da espira é acoplado a uma resistência de .
- Em qual posição da espira a corrente assume seu valor máximo? Justifique.
- Qual o valor da induzida máxima?
- Qual o valor e o sentido da corrente na primenta vez que atinge seu valor máximo, a partir da posição da figura.
Questão 28
Uma espira condutora quadrada de lado e resistência elétrica desloca-se em movimento retilíneo uniforme com velocidade (), de forma que dois de seus lados permanecem paralelos ao eixo , como mostrado na figura abaixo. Ela atravessa uma região de campo magnético uniforme e estacionário , que se estende ao longo de uma região de comprimento ao longo do eixo e por todo o eixo . Para os cálculos abaixo, escolha o vetor unitário (ou versor) normal à área definida pela espira como , ou seja, entrando no plano da folha.
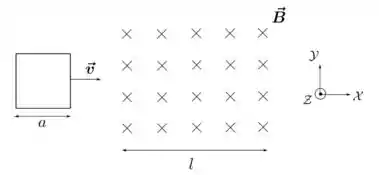
- Determine a intensidade e o sentido da corrente induzida na espira em três situações: quando ela está entrando na região do campo, quando está totalmente imersa nessa região e quando está saindo dessa região.
- Determine a força magnética sobre a espira (módulo, direção e sentido) nas mesmas três situações do item anterior.
- Faça gráficos separados da intensidade do fluxo de campo magnético sobre a espira e da corrente na espira como função do tempo . Considere o instante em que a espira começa a entrar na região do campo e destaque os intervalos de tempo correspondentes às três situações acima. Atribua sinais positivo e negativo para o sentido corrente de acordo com a orientação do vetor normal mencionado acima.
Questão 29
Uma espira quadrada condutora de lado é puxada, com aceleração constante, de uma região onde não existe magnético algum para outra região onde existe um campo magnético uniforme e estacionário perpendicular ao plano da espira. Durante o processo, a corrente induzida na espira:
- Será nula;
- Aumentará linearmente com o tempo;
- Será de algum valor constante diferente de zero;
- Aumentará exponencialmente com o tempo;
- Aumentará linearmente com o quadrado do tempo;
Questão 31
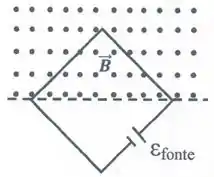
Um arame metálico, de resistência desprezível, forma um circuito circular, de raio , contendo um capacitor de capacitância , em série com um resistor de resistência igual a, como mostrado na figura 1. Este arame se encontra no plano x-y. A este sistema é aplicado um campo magnético, uniforme no espaço, dado por , onde e .
a) Calcule a instantânea sobre o aro como função do tempo.
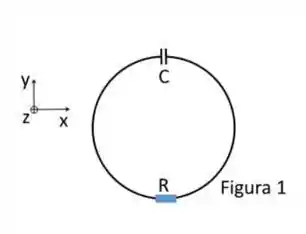 b) Supondo que, em t = 0 s, o capacitor estava descarregado e a corrente no aro era nula, obtenha a carga instantânea sobre o capacitor e a corrente sobre o aro como função do tempo.
b) Supondo que, em t = 0 s, o capacitor estava descarregado e a corrente no aro era nula, obtenha a carga instantânea sobre o capacitor e a corrente sobre o aro como função do tempo.
c) Calcule a potência total dissipada no resistor quando .
Ver solução completaQuestão 33
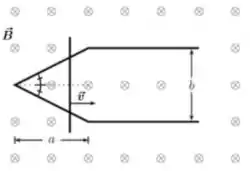
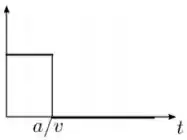
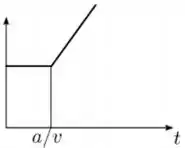
Uma barra condutora se move com velocidade constante e atrito desprezível sobre um par de trilhos condutores com a forma mostrada na figura abaixo. O sistema está imerso em um campo magnético constante que aponta para dentro do plano do papel. Sabendo que no instante a barra se encontra no ponto de cruzamento dos trilhos, qual dos gráficos abaixo melhor representa o comportamento do módulo do fluxo de campo magnético através da área definida pelo circuito como função do tempo ?
Escolha uma:
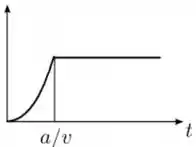
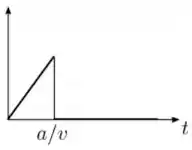
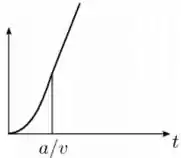
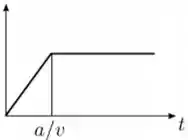
Questão 34
Uma bobina plana de 4 espiras tem área de e está orientada perpendicularmente a um campo magnético cuja intensidade aumenta uniformemente de a em . Qual a corrente induzida na bobina se a sua resistência é de ?
Ver solução completa
Questão 35
. Considere duas situações: na primeira, uma espira circular de área é atravessada perpendicularmente por um campo magnético uniforme que oscila periodicamente no tempo de acordo com a curva na figura abaixo (curva cheia), e na segunda situação a mesma espira é atravessada perpendicularmente por um campo magnético uniforme oscilante descrito pela curva (curva pontilhada). Podemos afirmar que a menor amplitude do fluxo de campo magnético e a maior amplitude da força eletromotriz induzida ocorrem, respectivamente, nas situações:
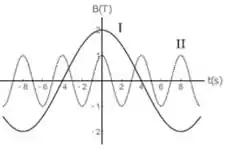
Escolha uma:
e
. e
. Não é possível determinar sem conhecer a resistência elétrica da espira
. e
. e
Ver solução completaQuestão 36
Um fio e um resistor de estão conectados formando uma malha quadrada de de lado. A intensidade do campo magnético varia linearmente de a em , em todos os pontos da malha.
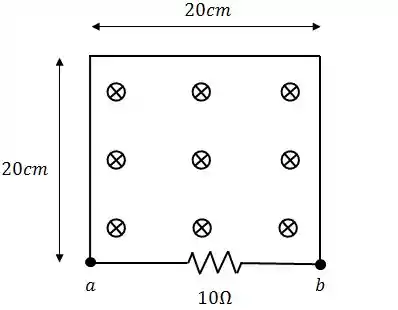
Qual a corrente induzida e o seu sentido ao percorrer o resistor?
, de para .
, de para .
, de para .
, de para .
, de para .
, de para .
Ver solução completaQuestão 38
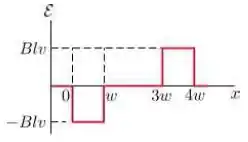
Uma espira condutora retangular de dimensões e se move com velocidade constante para a direita, conforme a figura.
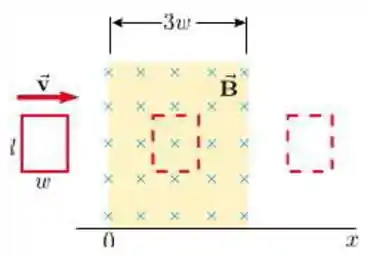
A espira atravessa um campo magnético uniforme e estacionário , dirigido para dentro da página, numa extensão de ao longo do eixo .
Assinale abaixo o gráfico que melhor representa a forca eletromotriz como função da posição da lateral à direita da espira:
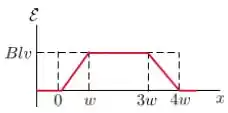
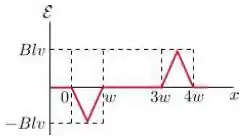
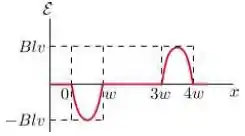
Questão 39
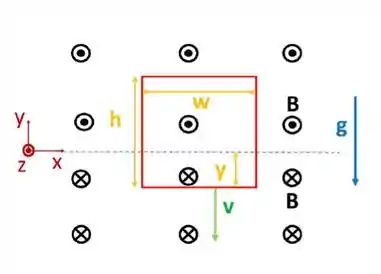
Uma espira retangular muito longa, de largura , resistência e massa , está inicialmente suspensa na presença de um campo magnético horizontal uniforme orientado para dentro do papel, que existe apenas acima do segmento de reta . Deixa-se cair a espira, que acelera sob ação da gravidade até atingir uma velocidade terminal .
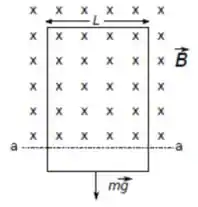
a) Calcule a força eletromotriz induzida na espira, em função dos dados acima e da sua velocidade.
b) Calcule a intensidade e determine o sentido da corrente induzida (explique a sua resposta) na espira, em função dos dados acima e da sua velocidade.
c) Obtenha uma expressão para ignorando a resistência do ar.
Ver solução completaQuestão 40
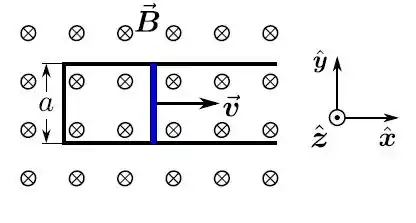
Um arame metálico forma um circuito retangular, de altura , largura e massa. Esse arame tem uma resistência total igual a . Na Figura, podemos ver que, em um certo instante de tempo, uma parte do aro está e outra em . O plano (linha azul tracejada) separa a região onde o campo magnético aponta na direção da região onde o campo magnético aponta na direção , como mostra a Figura. Observe a distância entre a linha tracejada azul e o braço horizontal inferior da espira.
Se , temos ; Se , .
Suponha que esse aro cai com velocidade vertical v constante sob a ação apenas de seu próprio peso e das forças magnéticas agindo sobre ele. Todas as respostas abaixo devem ser apresentadas apenas em função das variáveis do problema: (use apenas as necessárias).
Quando o aro está colocado como mostra a Figura, para todos os itens:
- Calcule a taxa de variação no tempo do fluxo magnético sobre o aro
- Calcule a sobre o aro e a corrente induzida. Seu sentido é horário ou anti horário? Justifique sua resposta
- Calcule a força magnética resultante sobre o aro
- Calcule o valor da velocidade constante com que o aro cai. Lembre-se que a velocidade é um vetor
- Calcule o valor da potencia elétrica dissipada no aro
- Calcule a potencia fornecida elo trabalho da força peso sobre o aro. Calcule
Questão 41
Em uma região de campo magnético uniforme , um aro condutor circular de raio está localizado no plano . Suponha que a resistência deste aro seja constante e igual a . Suponha que:
Onde é uma constante de tempo desconhecida.
- Desenhe um esquema mostrando o aro, a direção do campo magnético, a direção da corrente induzida no aro e a força sobre o aro devida ao campo magnético.
- Calcule o fluxo magnético e a sobre o aro. Obtenha expressões para a corrente induzida e para o valor da força magnética agindo sobre um segundo do aro de comprimento .
- Calcule a potencia instantânea dissipada no aro por efeito Joule.
- Suponha que forças externas agindo uniformemente sobre o aro, na direção radial, são responsáveis pelo aumento do raio do aro. Calcule a potência em um certo instante de tempo que as forças externas realizam sobre o aro. Despreze qualquer energia elástica do material que constitui o aro. É possível dizer que ? Justifique sua afirmação.
Questão 43
Q – O fluxo magnético de uma espira, em função do tempo, é dado por . A força eletromotriz induzida em seus terminais, para , é igual a:
.
.
.
.
.
Ver solução completaQuestão 44
Q - Uma corrente constante passa por um fio infinito conforme a figura. Um loop retangular está localizado ao lado e no mesmo plano do fio.
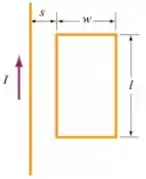
Calcule o fluxo magnético através do loop retangular. Existe uma fem induzida nesse caso? Por quê?
Suponha agora que a corrente depende do tempo como , onde e são constantes positivas. Qual será a fem induzida e qual o sentido da corrente induzida no loop retangular? Justifique suas respostas.
Ver solução completaQuestão 45
O circuito da figura está submetido a um campo magnético uniforme, perpendicular à pagina, apontando para fora.
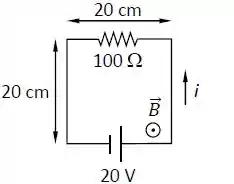
A corrente no circuito é , no sentido anti-horário. Podemos afirmar que a intensidade do campo magnético
aumenta a uma taxa de .
diminui a uma taxa de .
aumenta a uma taxa de .
diminui a uma taxa de .
aumenta a uma taxa de .
diminui a uma taxa de .
Ver solução completaQuestão 46
Uma espira retangular, de comprimento , largura e resistência , é colocada na vizinhança de um fio infinitamente longo que transporta uma corrente .
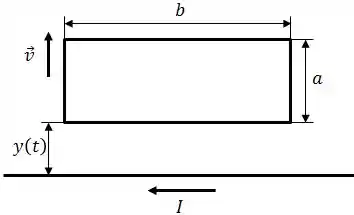
Suponha que a espira está se afastando do fio com uma velocidade constante . Considere que a distância inicial entre a espira e o fio vale .
Calcule o fluxo do campo magnético produzido pelo fio longo na espira em função da posição lateral .
Calcule a induzida e a corrente induzida na espira.
Considere agora o caso em que a corrente no fio infinito pode variar com o tempo. Para que a induzida na espira seja nula, essa corrente deve aumentar, diminuir ou se manter constante? Justifique.
Ver solução completaQuestão 47
A figura mostra uma espira condutora circular de raio , localizada no plano . A espira está submetida a um campo magnético variável no tempo e no espaço dado por , onde e são constantes positivas e é a distância radial até o centro da espira. O campo magnético atua na região hachurada da figura, sendo perpendicular à página e apontando para fora da mesma. Nestas circunstâncias, determine:
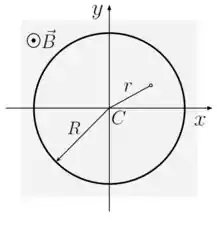
(a) O fluxo magnético através da espira.
(b) A força eletromotriz induzida na espira.
(c) O sentido de circulação da corrente induzida (horário ou anti-horário) num instante de tempo finito . Justifique sua resposta.
Ver solução completaQuestão 48
A figura abaixo mostra uma semi-circunferência de raio que gira com revoluções por segundo na presença de um campo magnético uniforme de . Sendo , determine a amplitude da corrente induzida no circuito.
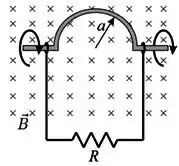
(a) .
(b) .
(c) .
(d) .
(e) .
Ver solução completaQuestão 49
O solenoide mostrado na figura tem duas espiras, seção reta de e um campo (paralelo ao eixo do solenoide) com magnitude dada por , onde está dado em segundos. Qual é o módulo da diferença de potencial para ?
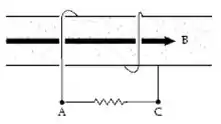
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 50
Uma barra condutora de comprimento desliza sem atrito sobre duas barras condutoras e paralelas (veja a figura abaixo). Um resistor está conectado como mostrado na figura. Um campo magnético constante está aplicado perpendicularmente à página. Um agente externo transporta a barra com velocidade . Qual o valor e o sentido da corrente que circula no circuito (ou seja, que atravessa o resistor de )?
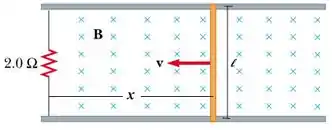
(a) no sentido anti-horário.
(b) no sentido horário.
(c) no sentido anti-horário.
(d) no sentido horário.
(e) no sentido anti-horário.
Ver solução completaQuestão 51
O circuito mostrado na figura, contendo um resistor de , está em um campo magnético uniforme que entra na página. A corrente no circuito é de no sentido horário. Qual a taxa de variação do campo magnético? Ele está aumentando ou diminuindo?
(a) Zero.
(b) e aumentando.
(c) e diminuindo.
(d) e diminuindo.
(e) e aumentando.
Ver solução completaQuestão 52
Uma espira quadrada com de lado é mantida perpendicular a um campo magnético uniforme com metade de sua área na região de campo, como mostra a figura. O módulo do campo magnético está variando de acordo com a equação , com em Tesla e em segundos. Ligada à espira, temos uma fonte de força eletromotriz (f.e.m.) com . Determine o valor da força eletromotriz total aplicada à espira o sentido da corrente em torno dela.
(a) , no sentido horário.
(b) , no sentido horário.
(c) , no sentido anti-horário.
(d) , no sentido anti-horário.
(e) , no sentido horário.
Ver solução completaQuestão 53
Um conjunto de espiras de cobre circulares de raio se situa num plano perpendicular a um campo magnético dependente do tempo. A variação do campo com o tempo é representada no gráfico. Qual o valor da fem induzida nesta espira?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 54
Uma espira quadrada de lado é percorrida por uma corrente no sentido anti-horário. A corrente varia com o tempo e é dada por , onde é uma constante.
(a) Usando a lei de Biot-Savart, calcule o vetor campo magnético produzido pela espira quadrada na origem do sistema de coordenadas.
(b) Considere um anel condutor de raio centrado na origem. Calcule a corrente induzida no anel pela espira quadrada e indique seu sentido. Considere que o anel possui resistência . Sugestão: Assuma que o campo magnético produzido pela espira quadrada é uniforme próximo à origem do sistema de coordenadas.
Ver solução completaQuestão 55
Um circuito fechado é formado por uma barra metálica de comprimento , que desliza com velocidade sobre um suporte metálico fixo, com uma resistência , imerso em um campo magnético uniforme e estacionário , perpendicular ao plano do circuito.
3a) A corrente induzida no circuito vale:
- 0,1 A
- 0,2 A
- 0,3 A
- 0,4 A
- 0,5 A
3b) A potência total entregue pelo agente externo para mover a barra:
- 0,5 W
- 2,0 W
- 2,5 W
- 3,0 W
- 5,0 W
Questão 56
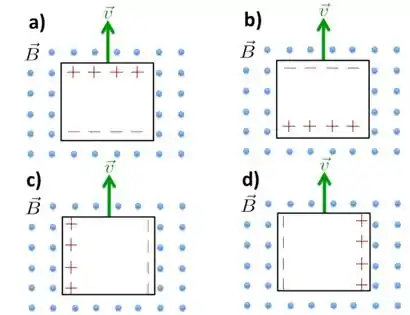
Uma placa condutora quadrada se desloca com velocidade constante, perpendicularmente a um campo magnético uniforme como indicada na figura abaixo. Qual dos diagramas representa a distribuição de cargas no condutor?
Questão 57
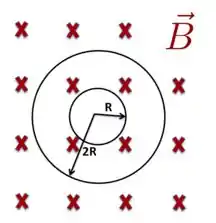
Um campo magnético uniforme, porém variável no tempo , induz uma força eletromotriz (fem) em uma espira de raio . Qual é a fem induzida na espira de raio ?
Questão 58
Um solenoide com comprimento muito maior do que o seu raio (solenoide ideal) tem o eixo de simetria coincidente com o eixo , e é atravessado por uma corrente (conhecida) em direção anti-horária (veja a figura).
A densidade linear de voltas do solenoide varia com a coordenada e é dada pela equação . Uma espira condutora circular de resistência elétrica e raio (conhecidos) é introduzida no solenoide e é colocada no instante de tempo no início do solenoide , para depois ser movida por um sistema não mostrado com velocidade constante positiva ao longo do eixo . A espira é completamente contida no solenoide (como mostrado na figura).
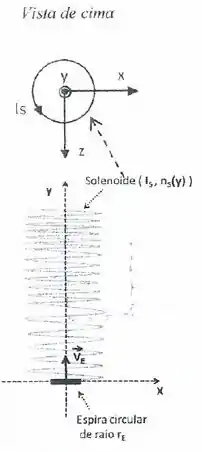
Nestas condições:
(a) Calcule em função do tempo o campo magnético (módulo, direção e sentido) gerado pelo solenoide no centro da espira.
(b) Calcule a corrente induzida na espira.
(c) Calcule o campo magnético (módulo, direção e sentido) gerado somente pela corrente induzida no centro da espira (Sugestão: utilize Biot e Savart). Qual será o campo magnético total no centro da espira?
Ver solução completaQuestão 59
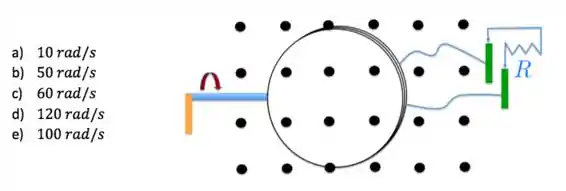
Uma bobina circular tem espiras e um raio de . A bobina é usada como um gerador de corrente alternada ao girar num campo magnético de , como mostra a figura. Qual é a velocidade angular com a qual se deve girar a bobina para que o valor máximo da fem seja de ?
Questão 60
Um capacitor formado por duas placas paralelas e circulares de raio , está sendo carregado. O campo elétrico em seu interior varia a uma taxa de . A corrente de deslocamento através das placas do capacitor vale, aproximadamente:
Questão 61
Uma espira condutora, quadrada, de lado está incialmente paralela ao plano de um sistema de coordenadas. Ela está imersa em uma região onde há um campo magnético uniforme e estacionário dado por . Considere, agora, três possíveis movimentos distintos para a espira:
- A espira é solta e cai em queda livre ao longo do eixo , permanecendo paralela ao plano
- A espira gira em torno de um eixo perpendicular a seu plano e que passa pelo seu centro.
- A espira gira em torno de um eixo que passa por um de seus lados.
Em quais dessas situações haverá uma corrente induzida na espira?
- Nenhuma delas
Questão 62
Considere uma espira circular, flexível e condutora de raio variável no tempo , imersa em um campo magnético uniforme, perpendicular ao seu plano. Para manter uma força eletromotriz variando linearmente com o tempo , o seu raio deveria variar de acordo com (onde é uma constante):
Questão 63
Um automóvel possui uma antena de rádio metálica de de comprimento, fixada na sua parte traseira. Considerando que, nessa região, o campo magnético da Terra é perpendicular à antena e vale , podemos afirmar que o valor máximo da fem induzida nessa antena quando o automóvel se desloca a uma velocidade de é:
Questão 64
Uma espira condutora de área é colocada em um campo magnético espacialmente uniforme, mas variável com o tempo, perpendicular ao plano da espira, como na figura. A induzida na espira é dada por , onde é uma constante. O módulo do campo magnético variável pode ser dado por:
Questão 65
Uma espira circular de de diâmetro, feita de fio de cobre (de resistência desprezível) tem ligado aos seus terminais uma resistência de , e é colocada num campo magnético uniforme de modo que o seu plano fique perpendicular ao vetor . Qual deve ser a taxa de variação de com o tempo para que a corrente induzida na espira seja igual a ?
Considere
Ver solução completaQuestão 66
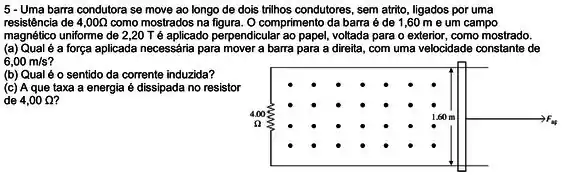
Uma barra metálica está se movendo com velocidade constante ao longo de dois trilhos metálicos paralelos, ligados por uma tira metálica numa das extremidades. Um campo magnético aponta para fora da página. Sabendo-se que os trilhos estão separados em e a velocidade escalar da barra é , que força eletromotriz (fem), em volts, é gerada?
Ver solução completaQuestão 67
Uma barra condutora de comprimento e resistência desprezível desliza sem atrito sobre dois trilhos condutores, como mostra a figura.
Dois resistores e são ligados às extremidades dos trilhos, fechando os dois circuitos. Um campo magnético uniforme está dirigido perpendicularmente para “dentro” da página. Um agente externo puxa a barra para a esquerda com velocidade constante.
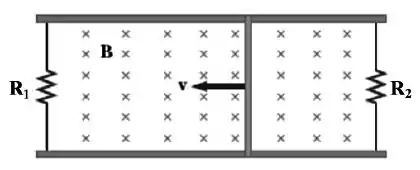
Encontre:
A potência total dissipada no circuito;
O valor e o sentido das correntes em ambos os resistores;
O vetor força magnética que age sobre a barra;
Ver solução completaQuestão 68
Dois trilhos paralelos condutores de resistência desprezível distam e são ligados por um resistor de . O circuito também contém uma barra de metal com resistência de , deslizando sobre os trilhos com velocidade constante de . Um campo magnético uniforme de é aplicado perpendicularmente ao plano dos trilhos, conforme figura.
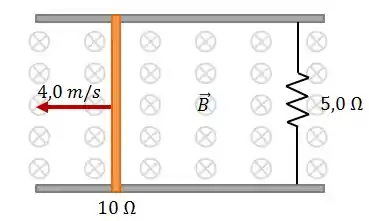
Calcule:
O valor e o sentido da corrente na barra;
O vetor força magnética que atua sobre ela;
A potência total dissipada no circuito;
Ver solução completaQuestão 69
Na figura abaixo dois trilho condutores retilíneos formam um ângulo reto. Uma barra condutora em contato com os trilhos parte do vértice no instante , com uma velocidade constante .
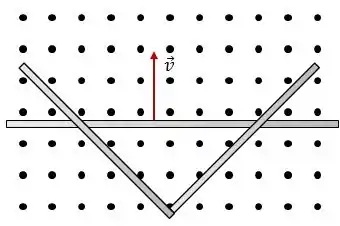
Há um campo magnético dirigido para fora da página, em toda a região. Determine:
- O fluxo magnético em função do tempo ;
- A induzida aplicada ao triângulo em função do tempo;
- Se a , onde e são constantes, e sabendo o valor de para , determine o valor de .
Questão 70
Uma espira quadrada de lado gira no sentido horário com velocidade angular em torno do eixo (que contém seu centro), numa região do espaço onde existe um campo magnético:
Onde .
A figura abaixo mostra uma vista superior da espira em rotação com velocidade . Observe que no instante a espira está contida no plano .
Num certo instante de o vetor de área faz um ângulo com o eixo .
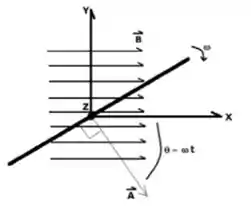
Calcule o fluxo magnético na espira quando .
Sabendo que a espira tem uma resistência elétrica de , calcule o valor da corrente induzida na espira no instante .
Suponha agora que o campo magnético comece a variar no tempo, de forma que:
Onde é igual à velocidade angular de rotação da espira.
Nestas condições. Calcule a frequência angular da corrente induzida.
[Sugestão: use a identidade trigonométrica ].
Ver solução completaQuestão 71
Uma barra condutora perfeita (com resistência nula) desliza sem atrito com velocidade , para a esquerda, sobre dois fios condutores também perfeitos. Dois resistores e estão conectados às extremidades dos dois fios, formando o circuito mostrado na figura. A distância entre os fios horizontais é , entre os resistores é , e da barra ao resistor é . Um campo magnético uniforme e constante de intensidade é aplicado perpendicularmente ao circuito, para fora da página. Ao calcular o fluxo magnético através de qualquer superfície, adote o vetor normal à superfície, na mesma direção e sentido do campo magnético.
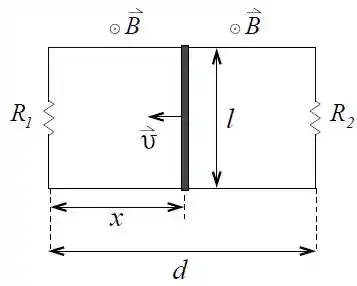
Determine o sentido (horário ou anti-horário) da corrente na porção do circuito à direita da barra justificando a sua resposta por meio da Lei de Lenz.
Calcule o fluxo magnético através da porção do circuito à direita da barra. Determine a corrente que atravessa o resistor por meio da Lei de Faraday.
Determine o sentido (horário ou anti-horário) da corrente na porção do circuito à esquerda da barra justificando a sua resposta por meio da Lei de Lenz.
Calcule o fluxo magnético através da porção do circuito à esquerda da barra. Determine a corrente que atravessa o resistor por meio da Lei de Faraday.
Calcule a intensidade e a direção da força magnética exercida sobre a barra. Essa força é de aceleração ou de frenagem?
Ver solução completaQuestão 72
4ª questão - Um campo magnético uniforme é aplicado perpendicularmente ao plano de uma bobina circular de espiras com raio de e resistência de . Se o campo magnético aumenta uniformemente de para em , qual é o módulo da induzida na bobina?
A)
B)
C)
D)
E)
Ver solução completaQuestão 73
Uma espira circular condutora de raio , contida no plano , transporta uma corrente no sentido anti-horário. Tal espira está sujeita a um campo magnético , onde é uma constante. Podemos afirmar que o módulo do fluxo magnético através da espira, , é dado por:
a)
b)
c)
d)
e)
Ver solução completaQuestão 74
. Uma espira retangular, rígida, de lados e , condutora, executa um movimento oscilatório ao longo da direção do eixo , de modo que a coordenada do seu centro é dada por:
onde é uma constante positiva e é um instante genérico. Além disso, temos um campo magnético constante de módulo que aponta para fora do plano da página, conforme mostra a figura abaixo .
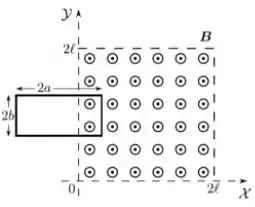
Considerando que o vetor normal ao plano da espira aponta no mesmo sentido do campo, definindo a orientação na qual a força eletromotriz induzida é positiva, em qual instante abaixo a força eletromotriz induzida na espira é máxima?
Escolha uma opção:
Ver solução completaQuestão 75
Uma barra de comprimento e resistência move-se com velocidade ao longo de trilhos horizontais condutores ideais (sem resistência) e sem atrito, conforme figura abaixo.
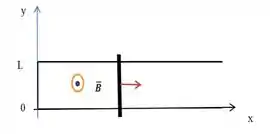
Supondo que , com , calcule a corrente induzida no circuito e a sua direção se e em temos .
Existe algum instante de tempo em que a corrente induzida seja zero? Se sim, qual? (justifique as suas afirmações).
Supondo que , calcule a corrente induzida no circuito indicando seu sentido em cada quadrante de , isto é, em se a posição da barra é dada por .
Ver solução completaQuestão 76
Considere uma espira circular, de raio , na presença de um campo magnético constante (uniforme e estacionário) , como mostra a figura. O vetor unitário , perpendicular ao plano da espira, forma um ângulo com o vetor unitário . Através da espira, circula uma corrente estacionária de intensidade , no sentido anti-horário. Determine o fluxo do campo magnético através da espira, o módulo da força magnética e o módulo do torque resultantes sobre ela.
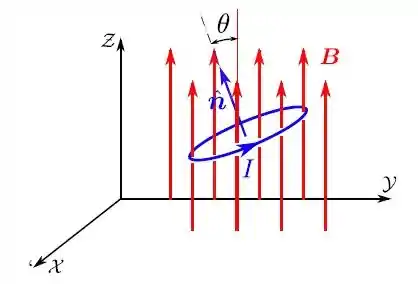
- , ,
- , ,
- , ,
- , ,
- , ,
- , ,
Questão 77
Um fio de massa , comprimento e resistência pode deslizar sem atrito, apoiado em dois trilhos horizontais, condutores e de resistência desprezível. Eles são ligados na extremidade esquerda por uma peça condutora, de modo que o conjunto todo forme uma espira condutora retangular.
Na região dos trilhos existe um campo magnético vertical uniforme e o fio de massa é puxado para a direita por uma força de módulo constante .
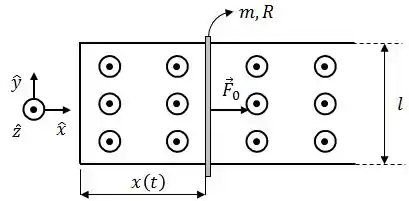
Calcule a e a corrente induzida no fio, indicando seus sentidos;
Calcule a força magnética que age sobre o fio, em função de sua velocidade;
Calcule a velocidade terminal (para ) do fio;
Quando o fio atinge essa velocidade, qual é a potência dissipada nele?
Ver solução completaQuestão 78
A figura abaixo mostra uma barra condutora de comprimento , deslizando para a direita, com velocidade constante , em contato com um fio, de modo a formar um circuito de resistência . Também está ilustrado na figura um campo magnético , constante e uniforme, saindo da página.
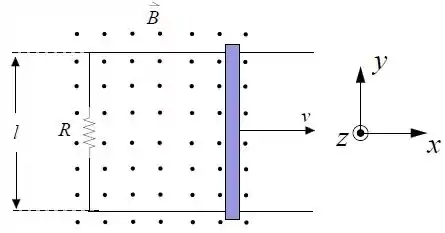
Determine o sentido da corrente induzida no circuito (horário ou anti-horário), justificando sua resposta.
Calcule a corrente induzida .
Calcule o vetor força externa que está sendo aplicada na barra de modo a manter sua velocidade constante.
Ver solução completaQuestão 80
Considere um condutor retilíneo de comprimento , movendo-se com velocidade constante igual a , dirigida perpendicularmente às linhas de um campo magnético uniforme, cuja magnitude é . O valor da força eletromotriz induzida nas extremidades do condutor é igual a:
Ver solução completaQuestão 81
Um pequeno corpo imantado está preso à extremidade de uma mola e oscila verticalmente na região central de uma espira cujos terminais A e B estão abertos, conforme indica a figura. Devido à oscilação do ímã, aparece entre os terminais A e B:
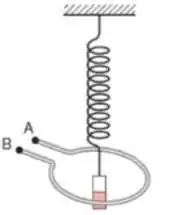
- Uma tensão e uma corrente elétrica, ambas constantes
- Uma corrente elétrica variável
- Uma tensão elétrica constante
- Uma tensão elétrica variável
- Uma corrente elétrica constante
Questão 82
Na figura abaixo, uma espira circular centrada no ponto carrega uma corrente com o sentido indicado na figura. Uma barra está em contato com um par de trilhos condutores circulares e gira ao redor do ponto com velocidade angular , como indicado na figura. Os trilhos são conectados por um resistor . Dadas as seguintes afirmações:
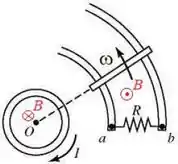
I. A corrente no resistor é nula.
II. A corrente no resistor flui de para .
III. A corrente no resistor flui de para .
IV. A direção da corrente no resistor depende do sentido de .
V. A magnitude da corrente no resistor depende da magnitude da corrente na espira circular.
Qual das alternativas abaixo lista todas as afirmações VERDADEIRAS?
(a) I.
(b) II e IV.
(c) III e V.
(d) II, IV e V.
(e) III, IV e V.
Ver solução completaQuestão 83
De acordo com a Lei de Faraday-Lenz, pode-se afirmar que:
- Existirá uma corrente elétrica induzida em uma espira circular quando houver variação no fluxo magnético que atravessa a espira;
- Se o fluxo magnético através da espira não variar com o passar do tempo, então, não haverá corrente induzida na espira;
- A corrente elétrica induzida em uma espira circular terá o mesmo sentido da variação do fluxo do campo magnético.
A única alternativa correta é?
- i e ii estão erradas e iii está correta
- i, ii e iii estão corretas
- i e iii estão corretas e ii está errada
- somente o item iii está correto
- i e ii estão corretas e iii está errada
Questão 84
Uma espira condutora quadrada de lado e resistência elétrica encontra-se sobre o plano de um sistema de coordenadas, com dois de seus vértices sobre os pontos e deste plano. Ela está imersa em uma região de campo magnético não-uniforme e não-estacionário dado por , onde é uma constante positiva.
(a) Determine a intensidade do fluxo de campo magnético através da área definida pela espira em um instante .
(b) Determine a intensidade e o sentido da corrente induzida no mesmo instante.
Ver solução completaQuestão 85
3ª questão - Enquanto um ímã é movido em direção à extremidade de um solenóide (como mostrado na Figura abaixo), uma diferença de potencial é induzida entre as duas extremidades do fio do solenóide. A diferença de potencial será maior se:
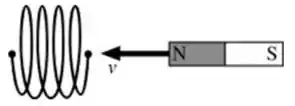
A) a velocidade do ímã for aumentada.
B) o solenóide contiver mais voltas (embora tivesse o mesmo comprimento).
C) o momento de dipolo magnético do ímã for mais forte.
D) Todas as afirmações acima são verdadeiras.
E) Nenhuma das afirmações acima são verdadeiras.
Ver solução completaQuestão 86
Uma espira circular está imersa em um campo magnético. O gráfico representa o fluxo magnético através da espira em função do tempo. O intervalo de tempo que aparece na espira uma corrente elétrica induzida é de:

(a) a , somente.
(b) a , somente.
(c) a .
(d) a , somente.
(e) a , somente.
Ver solução completaQuestão 87
Considere uma superfície fechada S, com vetor unitário normal apontando para fora. Sabendo que o fluxo de campo elétrico através de S é positivo, considere as afirmativas abaixo:
- Não pode haver partículas de carga negativa no interior de S.
- O campo elétrico deve necessariamente apontar para fora de S em todos os pontos dessa superfície.
- Não pode haver partículas de carga negativa no exterior de S.
São VERDADEIRAS as afirmativas:
- Nenhuma delas.
- I
- II
- III
- I e II
- I e III
- II e III
- I, II e III
Questão 88
Uma espira quadrada de lado igual a é colocada no interior de um solenoide que tem um comprimento de e espiras, conduzindo uma corrente de . Se a corrente no solenoide for reduzida a zero em , qual será aproximadamente a média induzida na espira quadrada?
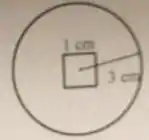
a) .
b) .
c) .
d) .
e) .
Ver solução completaQuestão 89
Uma espira quadrada se move com uma velocidade constante de uma região livre de campo para uma região de campo uniforme, como mostrado. Qual dos cinco gráficos mostra corretamente a corrente induzida no circuito em função do tempo ?
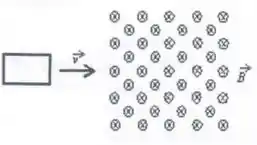
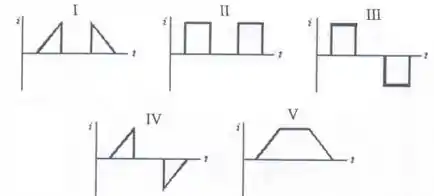
(a) I.
(b) II.
(c) III.
(d) IV.
(e) V.
Ver solução completaQuestão 90
Uma pequena espira com de área é colocada no interior de um solenoide longo com , percorrido por uma corrente senoidal com de amplitude e uma frequência angular de . Os eixos centrais da espira e do solenoide coincidem. Qual é, aproximadamente, a amplitude da força eletromotriz induzida na espira?
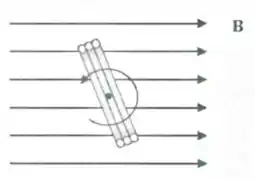
Ver solução completaQuestão 91
Uma bobina condutora consistindo de voltas de fio gira em torno de um eixo, paralelo ao plano da bobina e passando por seu centro, como mostra a figura. A bobina tem área e gira com uma velocidade angular constante em uma região onde há campo magnético uniforme e constante, que induz uma (variável no tempo) na bobina. Qual é a magnitude desta com função do tempo?
Questão 92
Em uma certa localidade o campo magnético da Terra tem modulo e uma inclinação pra baixo de em relação a horizontal. Uma bobina plana horizontal tem de raio, espiras e uma resistência total de e está ligada em série com um medidor com de resistência. A bobina descreve meia revolução em torno do diâmetro. Qual a carga que atravessa o medidor durante o movimento?
Ver solução completaQuestão 93
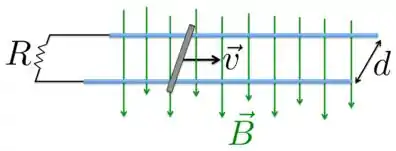
Trilhos paralelos condutores estão dispostos horizontalmente, distando um do outro, e são unidos por um resistor . Este aparato está em uma região onde há um campo magnético constante e uniforme, vertical e orientado para baixo. Uma barra condutora é puxada para a direita, sobre os trilhos sem atrito, com velocidade constante . A intensidade da corrente induzida é dada por
Questão 94
Considere as seguintes afirmativas:
Quanto maior é o fluxo de campo magnético através da superfície delimitada por uma espira, maior será a induzida nesta espira;
A induzida numa espira depende se esta é feita de um material condutor ou dielétrico;
A existência de induzida indica que forças magnéticas, desde que dependam do tempo, são capazes de realizar trabalho.
Nenhuma afirmativa está correta.
Apenas a afirmativa I está correta.
Apenas a afirmativa II está correta.
Apenas a afirmativa III está correta.
As afirmativas I e II estão corretas.
As afirmativas I e III estão corretas.
As afirmativas II e III estão corretas.
Todas as afirmativas estão corretas.
Ver solução completaQuestão 96
A resistência elétrica em uma espira circular influenciará: i) o valor da força eletromotriz induzida, já que a resistência elétrica é diretamente proporcional a corrente elétrica; ii) o valor da força eletromotriz induzida, já que a resistência elétrica é inversamente proporcional a corrente elétrica; iii) somente no valor da corrente elétrica induzida, já que a força eletromotriz induzida não depende do valor da resistência elétrica da espira.
Ver solução completaQuestão 97
Um pequeno corpo imantado está preso à extremidade de uma mola e oscila verticalmente na região central de uma bobina cujos terminais e estão abertos, conforme indica a figura. Devido à oscilação do imã, aparece entre os terminais e da bobina:
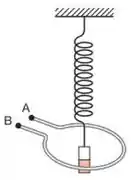
(a) uma corrente elétrica constante.
(b) uma corrente elétrica variável.
(c) uma tensão elétrica constante.
(d) uma tensão elétrica variável.
(e) uma tensão e uma corrente elétrica, ambas variáveis.
Ver solução completaQuestão 98
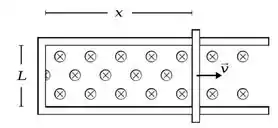
. Uma barra condutora fina se move com velocidade constante sobre um par de trilhos condutores finos, como mostrado na figura abaixo. O trecho em que os trilhos estão angulados tem um comprimento horizontal e a separação entre os trilhos no trecho em que eles são paralelos vale . No instante , a barra se encontra no ponto onde os trilhos se encontram. O atrito entre os trilhos e a barra é desprezível e todo o sistema está imerso em uma região de campo magnético constante .
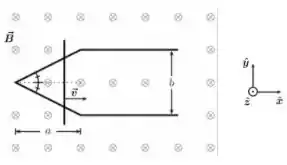
Determine o módulo do fluxo de campo magnético através da área definida pelos trilhos e a barra como função do tempo , considerando os intervalos e . Sugestão: Para o intervalo , utilize uma semelhança de triângulos para obter uma relação entre a porção de comprimento da barra dentro do circuito e o seu deslocamento horizontal.
Determine o módulo e o sentido da força eletromotriz induzida no sistema como função do tempo , considerando os mesmos intervalos.
(c) Esboce os gráficos dos módulos do fluxo e da força eletromotriz induzida como função de , destacando os valores relevantes.
Ver solução completaQuestão 99
12 - Uma haste com resistência repousa sobre trilhos condutores sem atrito em um campo magnético uniforme constante , como mostrado. Suponha que os trilhos tenham resistência desprezível. A magnitude da força que deve ser aplicada por uma pessoa para puxar a haste para a direita a velocidade constante é:
Questão 100
Um fio fino, retilíneo e infinito transporta uma corrente estacionária de intensidade , no sentido indicado na figura abaixo. Três espiras quadradas, , e , posicionadas no mesmo do plano do fio e com dois de seus lados paralelos a ele, se movem com velocidade constante nos sentidos indicados. As espiras e são condutoras, enquanto a espira é perfeitamente isolante. Em quais dessas espiras há uma força eletromotriz induzida?
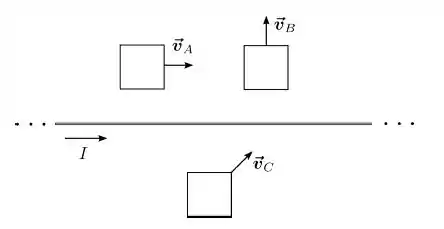
- Apenas B e C
- Apenas A
- Apenas B
- Apenas C
- Apenas A e B
- Apenas A e C
- A, B e C
- Nenhuma delas
Questão 101
Uma barra condutora se move com velocidade constante e atrito desprezível sobre um par de trilhos condutores com a forma mostrada na figura abaixo. O sistema está imerso em um campo magnético constante que aponta para dentro do plano do papel. Sabendo que no instante a barra se encontra no ponto de cruzamento dos trilhos, quais dos gráficos abaixo melhor representam o comportamento dos módulos do fluxo de campo magnético e da força eletromotriz induzida no circuito como função do tempo , respectivamente?
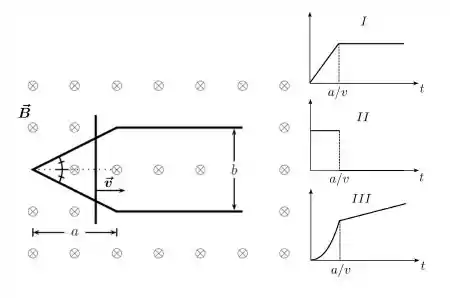
- III e I
- I e II
- II e I
- I e III
- II e III
- III e II
Questão 102
A barra condutora de comprimento e massa cai no campo gravitacional escorregando sem atrito sobre um fio condutor na forma de um ligado a um resistor de resistência , conforme a figura. O conjunto forma um circuito na vertical que se encontra na presença de um campo magnético uniforme na direção perpendicular ao plano do circuito.
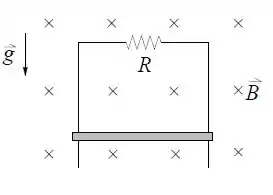
- Qual é o sentido da corrente induzida no circuito? Justifique.
- Calcule a f.e.m. induzida no circuito em termos do módulo da velocidade instantânea da barra na direção vertical.
- Determine a velocidade terminal da barra e a corrente que passa no circuito quando ela se encontra neste velocidade.
- Calcule a potência dissipada pelo sistema na situa do item (c) e mostre que ela é igual à potência fornecida ao sistema pelo campo gravitacional.
Questão 103
Considere uma espira retangular de lado maior e de lado menor , situada no plano xy (veja figura abaixo). Aplica-se um campo magnético externo que varia no tempo de acordo com a expressão , onde é uma constante dada em e é o tempo em .
(a) Calcule a magnitude do fluxo magnético, através da espira.
(b) (1,0 ponto) Qual é o sentido da corrente induzida na espira (horário ou anti-horário)? Justifique sua resposta!
(c) (0,5 ponto) Supondo que a espira tenha resistência , calcule a magnitude da corrente induzida, , em um instante qualquer.
Questão 104
Um campo eletrostático é definido por:
Onde , e são constantes positivas. Considere abaixo:
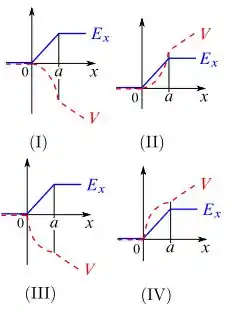
Supondo que o potencial se anula na origem, qual deles melhor representa ?
- O gráfico (I)
- O gráfico (II)
- O gráfico (III)
- O gráfico (IV)
- Nenhum deles
Questão 105
Considere duas situações: na primeira, uma espira circular de área é atravessada perpendicularmente por um campo magnético uniforme que oscila periodicamente no tempo de acordo com a curva na figura abaixo (curva cheia), e na segunda situação, a mesma espira é atravessada perpendicularmente por um campo magnético uniforme oscilante descrito pela curva (pontilhada). Podemos afirmar que a maior amplitude do fluxo de campo magnético e a maior amplitude da fem induzida ocorrem, respectivamente, nas situações
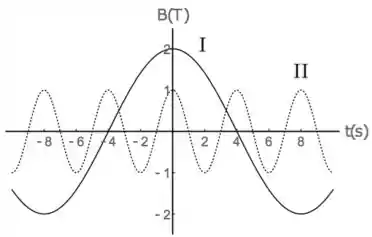
- Não é possível determinar sem conhecer a resistência elétrica da espira.
Questão 106
Considere uma espira condutora imersa em um campo magnético permanente, gerado pelos pólos de um ímã.
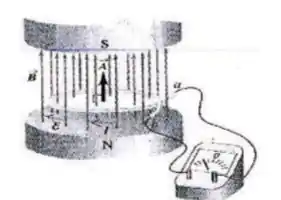
O módulo do campo magnético aumenta a uma taxa de . A área desta espira é igual a e ela está ligada a um galvanômetro, sendo que a resistência total deste circuito é de . A corrente que indicará no galvanômetro será de:
Ver solução completaQuestão 107
Um campo magnético uniforme faz um ângulo de com o eixo de uma espira circular de 300 voltas e um raio de . O campo varia a uma taxa de . Determine o módulo da fem induzida na espira
Ver solução completaQuestão 108
Uma barra metálica neutra está se movendo com velocidade constante para a direita, em uma região onde há um campo magnético constante apontando perpendicularmente para fora da página. Qual dos seguintes diagramas descreve melhor a distribuição de cargas na superfície da barra metálica?
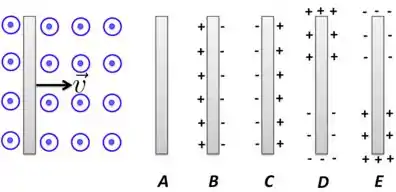
- A;
- B;
- C;
- D;
- E.
Questão 109
O anel de resistência elétrica , contido no plano , é constituído por um condutor elástico, o que possibilita variações de seu raio .
Durante o intervalo de tempo o raio do anel diminui segundo a equação , onde é constante. O campo magnético presente na região é uniforme e ortogonal ao plano .
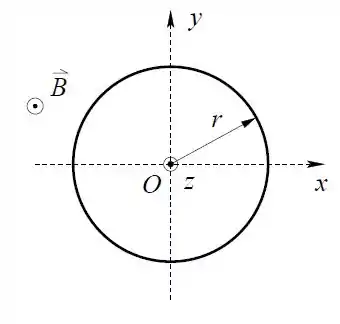
Nas perguntas abaixo considere o tempo apenas no intervalo .
Determine a força eletromotriz induzida no anel em função de .
Calcule a corrente induzida no anel e determine o seu sentido (horário ou anti-horário).
Calcule o campo magnético produzido pela corrente induzida no centro do anel. Se você não resolveu o item deixe sua resposta em função da corrente induzida .
Ver solução completaQuestão 110
A barra de comprimento e resistência está apoiada sobre o trilho fixo, indeformável e de resistência desprezível, conforme mostra a Figura. Os lados e são muito longos. O fio muito longo e retilíneo alinhado com o eixo conduz a corrente constante . Um agente externo exerce uma força de módulo sobre a barra, que a afasta do fio com velocidade constante no sentido positivo do eixo , de modo que .
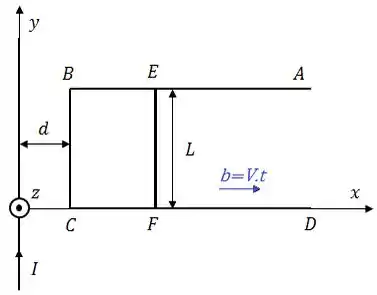
Determine o vetor campo magnético gerado pelo fio muito longo em um ponto arbitrário do semipleno .
Calcule o fluxo magnético através da espira em função dos dados fornecidos.
Calcule a corrente induzida na espira em função dos dados fornecidos e, justificando, indique seu sentido (horário ou anti-horário).
Ver solução completa