Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Oscilador Linear Massa-Mola

Ver Todos os Exercícios

Teoria

Fala aí! Seja bem vindo ao Responde Aí! Bora aprender tudo sobre Sistema Massa-Mola?

Oscilador Linear Massa-Mola

O sistema massa mola pode ser representado pelo oscilador linear que podemos observar na figura abaixo:

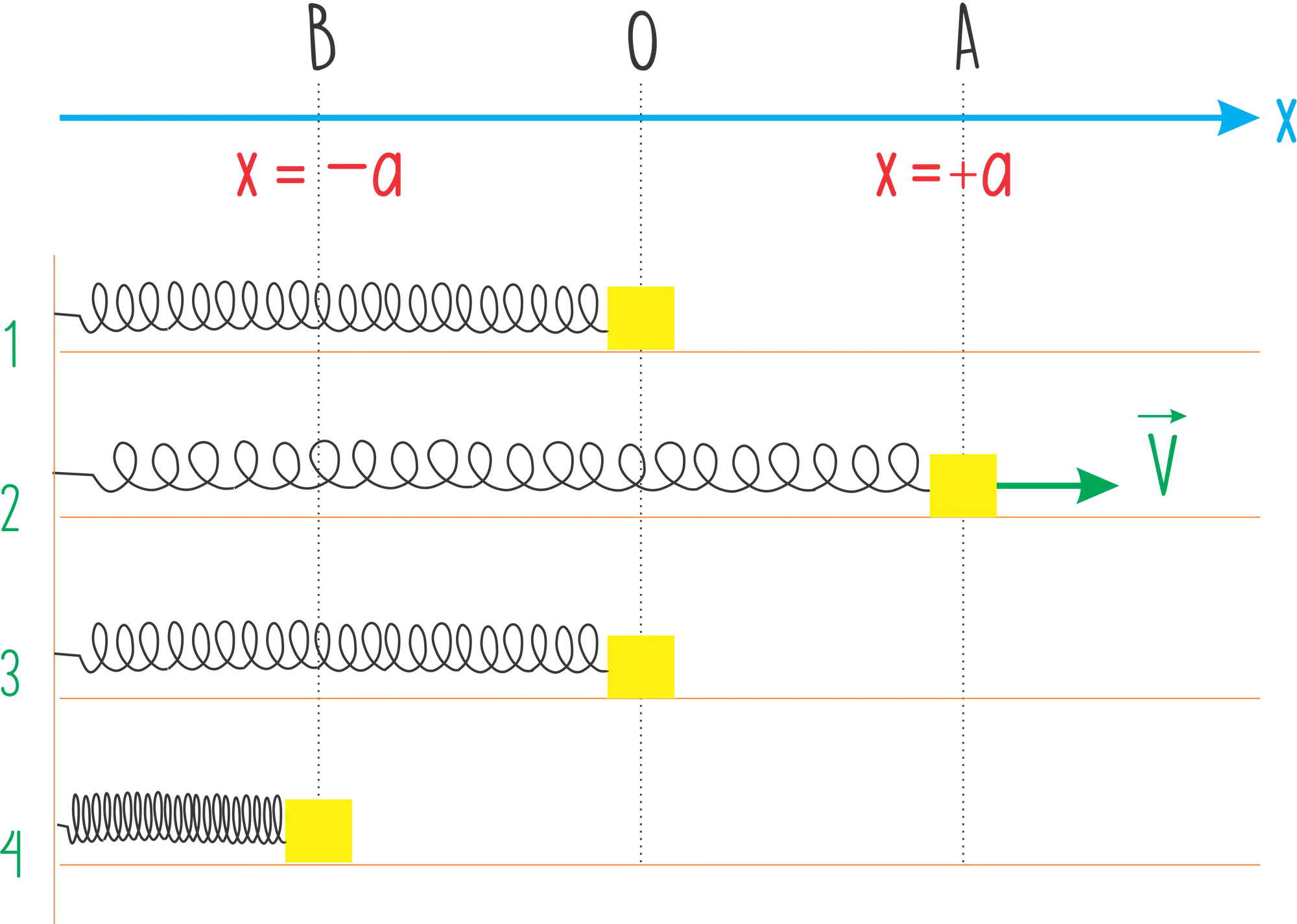
Oscilador linear massa-mola
Oscilador linear massa-mola

A gente pode observar um bloquinho de massa preso a uma mola com constante elástica . Em um primeiro momento o nosso bloquinho esta em equilíbrio, na posição . Quando damos uma puxadinha no bloco a mola se deforma e quando soltamos ela rapidamente se comprime.

Podemos dizer que esse sistema realiza um movimento harmônico simples (MHS), de amplitude , com extremos e . Logo, vale a seguinte equação pra descrever seu movimento:

Onde:

  • é a amplitude do movimento;
  • é a frequência angular;
  • é a fase do movimento;

-Hãam?! 😖

Calma, a gente vai explicar tudo tim tim por tim tim! E pra começar com o pé direito a gente preparou esse vídeo super completo sobre Sistema massa-mola. Dá só uma conferida!

Oscilador Massa-Mola: Fórmulas

Existem algumas equações muito importantes que vamos usar bastante no sistema massa-mola! Bora conhecer elas?

Força Elástica

A força elástica é dada por:

á

Onde é a constante da mola e é o deslocamento. Esse sinal de menos na fórmula é uma correção, afinal a força elástica sempre vai ser contrária a elongação. Por exemplo: se você tiver puxando a mola pra direita, surgirá uma força elástica apontando pra esquerda.!

EDO do MHS

Para descrever o movimento harmônico simples do sistema massa mola, também podemos usar a seguinte EDO:

Aqui o é a derivada segunda da posição, que representa a aceleração instantânea do bloco.

Exemplo: Calcule a constante da mola, considerando um sistema massa-mola com um bloco de 20 kg em um movimento que se repete a cada 2 segundos

Se o movimento se repete a cada dois segundos, então esse é seu período . Podemos então usar a seguinte fórmula:

Isolando o :

Substituindo nossos dados:

Prontinho! Agora vamos praticar com exercícios?

Oscilador Massa-Mola: Fórmulas

Exemplo: Calcule a constante da mola, considerando um sistema massa-mola com um bloco de 20 kg em um movimento que se repete a cada 2 segundos

Exercícios Resolvidos

Exercício Resolvido #1

Um sistema massa-mola consiste em um bloco de massa 5 00   g preso a uma dada mola. Sabe-se que o sistema oscila com amplitude de 20 , 0   c m e que ele repete seu movimento a cada 0 , 5   s . Suponha que a posição seja dada por x t = A . cos ⁡ ( ω . t + ϕ ) . Se a posição do bloco em t = 0,120   s é a maior possível, determine:

a ) O período T e a frequência angular do movimento;

b ) A constante da mola;

c ) A velocidade máxima;

d ) A constante de fase ϕ ;

Passo 1

a )

O período é o tempo necessário para que um ciclo se complete, pelo enunciado, temos que:

T = 0 , 5   s

Agora que sabemos o período, fica molezinha determinar a frequência angular:

ω = 2 . π T

ω = 2 . π 0 , 5 = 4 . π ≈ 12,57   r a d / s

Passo 2

b )

Agora que já calculamos a frequência angular, vamos determinar a constante elástica da mola...basta lembrar que:

ω = k m

Substituindo, temos

k = m . ω 2

k = 0 , 5 . 12,57 2

k ≈ 79,00   N / m

Passo 3

c )

Para determinar a velocidade máxima do oscilador, precisamos lembrar como funciona esse negócio! O sistema, quando em posição de mínimo ou máximo, tem que sua energia mecânica é puramente elástica:

E m e c = E e l = k . x 2 2

E valerá:

E m e c = E e l = k . A 2 2 = 79 . 0 , 2 2 2

E m e c = 1 , 58   J

Quando o oscilador estive passando por x = 0 , temos que a energia mecânica será puramente energia cinética, e valerá:

K = m . v 2 2 = E m e c

Substituindo, temos:

0 , 5 . v 2 2 = 1 , 58

v = 2 , 51   m / s

Passo 4

d )

Para determinar a constante de fase, vamos olhar pra cara da função x ( t ) . Das informações que já temos, fica:

x t = A . cos ⁡ ω . t + ϕ

x t = 0 , 2 . cos ⁡ 4 π . t + ϕ

O enunciado nos diz que para t = 0,120   s , x é máximo, ou seja:

x t = 0,12 = 0 , 2

x t = 0,12 = 0 , 2 . cos ⁡ 4 π . 0,12 + ϕ = 0 , 2

cos ⁡ 0,48 π + ϕ = 1 → 0,48 π + ϕ = 0

ϕ = - 0,48 π

Resposta

a )   T = 0 , 5   s ;     ω = 4 π ≈ 1 2 , 57   r a d / s

b )   k = 79   N / m

c )   v = 2 , 51   m / s

d )   ϕ = - 0,48 π

Exercício Resolvido #2

Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 105-7

Um oscilador é formado por um bloco com uma massa de   0,500   k g ligado a uma mola. Quando é posto em oscilação com uma amplitude de 35,0   c m o oscilador repete o movimento a cada 0,500   s . Determine:

(a) o período

(b) a frequência

(c) a frequência angular

(d) a constante elástica

(e) a velocidade máxima

(f) o módulo da força máxima que a mola exerce sobre o bloco.

Passo 1

a)

Se o movimento se repete a cada 0,5   s , esse é o período:

T = 0,5 s

Passo 2

b)

A frequência será o inverso do período:

f = 1 T = 1 0,5 = 2   H z

Passo 3

c)

Com o valor do período, basta fazer:

ω = 2 π T = 2 π 0,5 = 4 π   r a d / s

Passo 4

d)

A constante elástica será dada por:

ω = k m → k = ω 2 m = 4 π 2 0,5 = 78,9   N / m

Passo 5

e)

A velocidade máxima é dada por:

v m á x = ω A = 4 π . 35.10 - 2 = 4,39   m / s

Passo 6

f)

Pra achar a força máxima, precisamos achar a aceleração máxima:

a m á x = ω 2 A = 4 π 2 35.10 - 2 = 55,26   m / s 2

Isso vezes a massa nos dá a força máxima:

F m á x = m a = 0,5.55,26 = 27,63   N

Obs.: Reparem que poderíamos ter calculado a força máxima exercida pela mola pela definição de força de uma mola elástica para a sua deformação máxima, que no caso é o valor da amplitude. Dessa forma, teríamos F m á x = k   .   A = 78,9   .   0,35 = 27,63   N .

Resposta

  1. 0,5 s
  2. 2   H z
  3. 4 π   r a d / s
  4. 78,9   N / m
  5. 4,39   m / s
  6. 27,63   N

Exercício Resolvido #3

Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 106-7

Uma pedra de 50,0   g   está oscilando na extremidade inferior de uma mola vertical. Se a maior velocidade da pedra é 15,0 cm/s e o período é de 0,500 s , determine:

(a) a constante elástica da mola

(b) a amplitude do movimento

(c) a frequência da oscilação.

Passo 1

a)

Usando o período, podemos descobrir a frequência angular:

ω = 2 π T = 2 π 0,5 = 4 π

Assim, usando a relação:

ω 2 = k m → k = m ω 2 = 50.10 - 3 . 4 π 2 = 7,89   N / m

Passo 2

b)

Se a velocidade máxima da pedra é dada por:

v m á s x = ω A

Como já sabemos ω :

A = v m á x ω = 15.10 - 2 4 π = 1,19.10 - 2 m = 1,19 c m

Passo 3

c)

A frequência linear será dada por:

f = 1 T = 1 0,5 = 2 H z

Resposta

a)

7,89   N / m

b)

1,19 c m

c)

f = 2 H z

Exercício Resolvido #4

USP-P1-2014-Q3

As missões Apollo 15, 16 e 17 levaram um jipe para a superfície lunar. Esse jipe quando totalmente carregado possui uma massa M , a mola da suspensão possui uma frequência natural de oscilação de 1   H z medidos na superfície terrestre. Sabendo que a aceleração da gravidade na superfície lunar equivale a 1 / 6 ao da aceleração na superfície terrestre, pode-se afirmar que a frequência natural de oscilação da suspensão do jipe na superfície lunar é

  1. f 0 = 6   H z
  2. f 0 = 1 / 6   H z
  3. f 0 = 6   H z
  4. Depende da massa do jipe, M
  5. f 0 =   1 / 6   H z

Passo 1

Antes de fazermos a questão, preste atenção nisso:

f 0 : Frequência natural de oscilação.

ω 0 : Frequência angular natural de oscilação.

Existem outros nomes pra essas frequências, é claro, mas essas são as mais usadas.

A frequência natural que o enunciado faz referência é o f 0 .

A gente sabe que ω 0 pode ser calculado por:

ω 0 = k M

Assim:

ω 0 = 2 π f 0 → f 0 = ω 0 2 π = 1 2 π k M

Logo, a frequência apenas depende da constante da mola e da massa do sistema.

E o que isso quer dizer, meu amigo? Que a frequência de oscilação lá na lua vai ser igual a daqui da Terra.

Então:

f 0 = 1 2 π k M

A frequência só depende da massa do jipe e da constante de mola. =)

Resposta

d)

Exercício Resolvido #5

Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 107-14

Um oscilador é formado por um bloco preso a uma mola ( k = 400   N / m ). Em um certo instante t a posição (medida a partir da posição de equilíbrio do sistema), e a aceleração do bloco são x = 0,100   m , e a = - 123   m / s 2 . Calcule

(a) a frequência de oscilação,

(b) a massa do bloco

Passo 1

a)

Como a função posição é dada por:

x t = A c o s ω t + φ

E a aceleração é dada por:

a t = - ω 2 A cos ⁡ ω t + φ

Podemos dizer que:

a t = - ω 2 x t

Sacou? Só jogamos x t ali pra baixo, na equação de a t .

Passo 2

Então, vamos usar o valor de x = 0,100 m e o valor da aceleração nesse ponto pra descobrir a frequência angular:

- 123 = - ω 2 . 0.100 → ω 2 = 1230 → ω = 35,07   r a d / s

Essa é a frequência angular. A frequência linear será:

ω = 2 π f → f = ω 2 π = 35,07 2 π = 5,58   H z

Passo 3

b)

A massa do bloco pode ser determinada se a gente usar a relação:

ω = k m → m = k ω 2 = 400 35,07 2 = 0,325   k g

Resposta

a)

ω = 35,07   r a d / s → f = 5,58   H z

b)

0,325   k g

Exercícios de Livros Relacionados

Na figura, um bloco pesando 14,0N , que pode deslizar sem atrito em um plano inclinado de ângulo θ = 40,0 ° , está ligado ao alto do plano inclinado por uma mola de massa desprezível de 0,450m de comp
Um oscilador é formado por um bloco preso a uma mola ( k = 400N / m ). Em um certo instante t , a posição (medida a partir da posição de equilíbrio do sistema), a velocidade e a aceleração do bloco sã
Um bloco de 1,2k g deslizando em uma superfície horizontal sem atrito está preso a uma mola horizontal com k = 480N / m . Seja x o deslocamento do bloco a partir da posição na qual a mola se encontra
A figura mostra uma massa de 1,0k g colocada sobre uma massa de 5,0k g que oscila sobre uma superfície sem atrito. A constante elástica é de 50N / m , e o coeficiente de atrito estático entre os dois
A figura mostra um bastão homogêneo de 200g com um orifício em uma das extremidades. A outra extremidade é presa a uma mola horizontal. Quando o bastão está suspenso exatamente na vertical, a mola não