Associação de Molas
Produzido por Leonardo de BemTeoria
Fala aí! Hoje vamos aprender sobre associação de molas e como adaptar a lei de Hooke para molas em série ou em paralelo. A ideia é você sair daqui sabendo resolver um problemão desse tipo aqui:

Tá preparado? Então vem comigo!
Ah, vou deixar aqui embaixo alguns links de conteúdos prévios a esse aqui que são importantes pra você chegar arrasando. O primeiro trata da força elástica e da lei de Hooke com um pouco mais de detalhes do que vou abordar aqui!
⭐ Veja também ⭐
Lei de Hooke
A lei de Hooke estabelece uma proporção entre a força elástica (
Aquele k que aparece ali é a constante elástica. Esse cara vai ser o personagem principal aqui quando começarmos a tratar de associações.
Associação de Molas em Paralelo
Quando posicionamos molas lado a lado conectadas ao mesmo objeto, dizemos que elas estão associadas em paralelo.

Nessa imagem eu coloquei só duas molas, mas poderíamos associar muito mais, beleza?
O que eu quero que você repare é como ambas as molas sofrerão a mesma deformação quando uma força for aplicada ali naquela caixa.
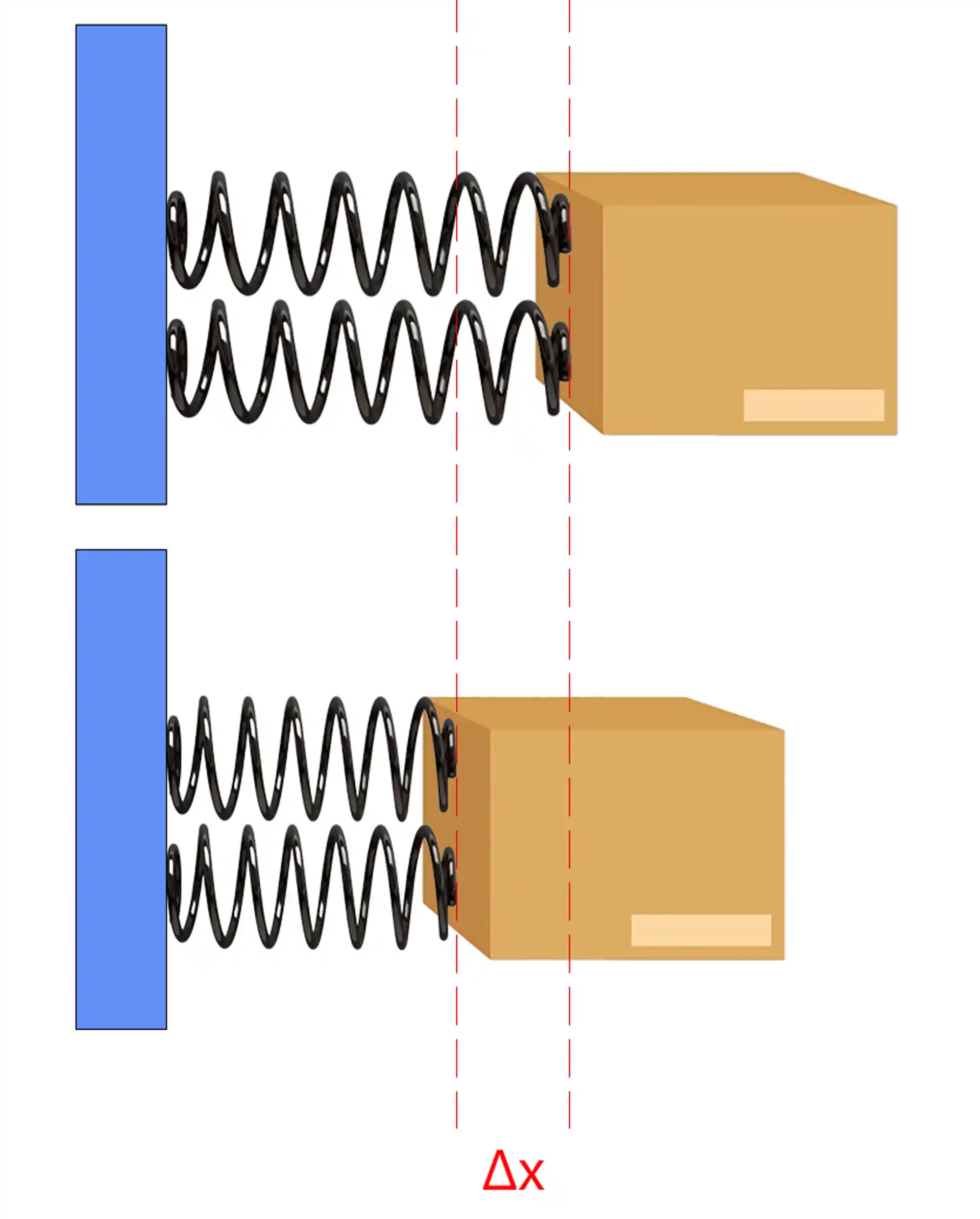
Importante: embora pareça intuitivo, a força elástica de cada mola não é a mesma. Pois, se elas tiverem constantes elásticas diferentes, exercerão resistências à deformação também diferentes!
Vamos chamar a mola de cima de mola 1 e a de baixo de mola 2. Com isso, podemos equacionar a lei de Hooke para cada uma:
Se somarmos as duas equações, podemos encontrar a força elástica total:
Só que, ali na imagem anterior, a gente percebeu que a deformação
E a força total também pode ser dada pelo produto de constante elástica equivalente e da deformação total:
Então:
Agora a gente pode cortar aquele
E assim a gente conclui que, para molas associadas em paralelo, a constante elástica equivalente é a soma das constantes individuais de cada mola.
E novamente, isso vale para qualquer número de molas!
Molas Associadas em Série
Agora, para associarmos molas em série, devemos posicioná-las em sequência, como nesse exemplo aqui:
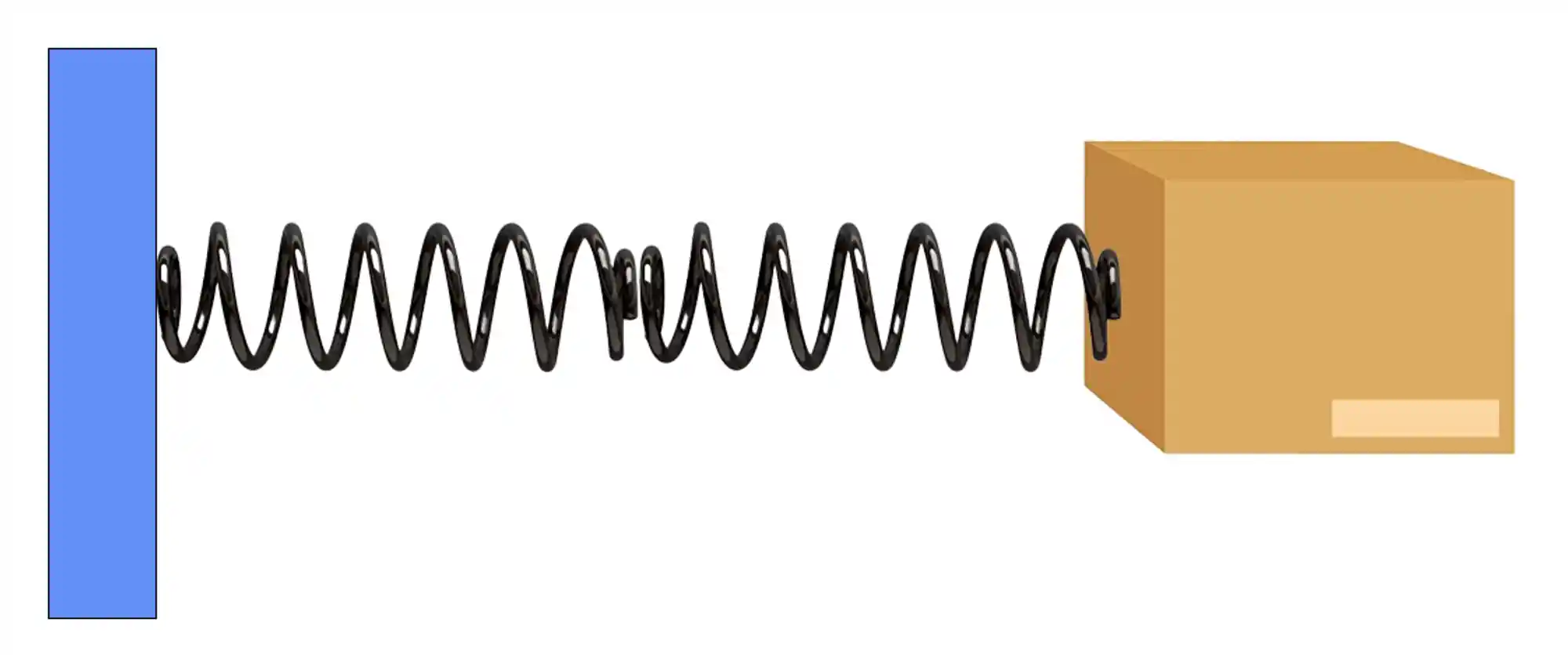
A sacada aqui é outra: a deformação sofrida por cada mola não é a mesma, mas a força aplicada sobre elas, é!
Ao aplicar uma força, seja puxando ou empurrando a caixa, a primeira mola (conectada à caixa) começa a deformar e exerce uma força elástica puxando ou pressionando a segunda mola. E assim por diante, para quantas molas estiverem associadas!
A gente ainda pode chamar a soma das deformações de uma deformação total
E a força exercida sobre cada mola é a mesma, como descobrimos ali pela análise da figura. Então, a gente pode fazer assim:
Aí a gente pode escrever aquela relação anterior (das somas das deformações) em termos da força e da constante:
Como as forças são todas iguais e comuns para todas as parcelas, podemos cortá-la.
E assim a gente consegue encontrar a constante equivalente para molas associadas em série!
Novamente, vale lembrar que isso vale para qualquer número de molas.
Associação de Molas em Série e em Paralelo
Se tivermos uma situação com um conjunto de molas associadas tanto em série quanto em paralelo, devemos fazer uma análise mais cuidadosa. O segredo é começar sempre pelo menor número de associações.
Por exemplo, se tivermos uma situação como aquela que te mostrei lá no início da página, começamos a análise pelas molas associadas em paralelo para obter as resultantes. Depois disso, fazemos a análise das molas associadas em série com essas resultantes!
Belezinha? Agora é a hora de praticar com alguns dos nossos exercícios resolvidos passo a passo!
Molas Associadas em Série
Associação de Molas em Série e em Paralelo
Exercícios Resolvidos
Exercício Resolvido #1
UERJ- Lista para P1- Lista de Oscilações- 9
Na figura, duas molas são ligadas e conectadas a um bloco de massa que é posto em oscilação sobre um piso sem atrito. Cada uma das molas possui constante elástica . Qual é a frequência das oscilações?
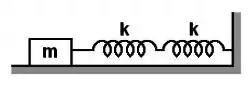
Passo 1
Primeiramente, vamos descobrir a constante da mola resultante da associação em série das molas da figura. Como elas estão em série, usaremos:
Com
Passo 2
Agora a gente precisa encontrar a frequência de oscilação! Bom, você lembra qual equação relaciona a constante da mola à velocidade angular? Esta aqui:
E a frequência angular pode ser escrita como:
Onde é a frequência de oscilação! Unindo as duas equações:
Substituindo , e calculando, obtemos:
Tranquilo, não é verdade? (:
Resposta
Exercício Resolvido #2
UNICAMP-Questão 1 - P2.2010 Noturno
Um bloco de massa , em repouso numa mesa horizontal sem atrito, é ligado a um suporte rígido por duas molas de constante elástica e . Uma bala de massa e velocidade atinge o bloco como mostrado na figura abaixo.
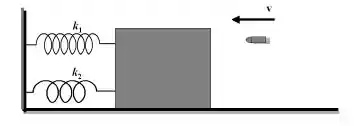
Este sistema de duas molas da figura acima é equivalente a um sistema composto por apenas uma mola cuja constante elástica vale:
- Deduza a expressão .
- A velocidade do bloco imediatamente após a colisão.
Agora, considere e determine em função de , , :
Passo 1
a)
Vamos deduzir partindo da força resultante que as duas molas fazem sobre o bloco:
Sendo:
Logo:
Beleza! Mas será que existe uma relação entre os s?
Bom, como o bloco não tomba nem vai se deslocar torto, o deslocamento de cada mola deve ser igual, lembra? Vamos dar uma olhada na figura:
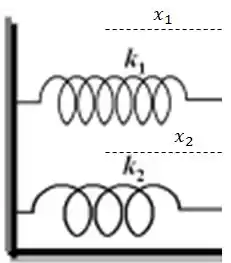
Caso a caixa tombaria pra frente, por exemplo. Logo:
O deslocamento da força resultante também deve ser igual. Isso acontece por que o significado da associação de molas nos diz que as duas molas poderiam ser substituídas por uma única mola cuja constante é a constante resultante.
E qual seria o deslocamento dessa mola? Fica claro que deveria ser o mesmo que o das duas molas, não é?
Logo:
Passo 2
b)
Vamos resolver essa parte usando a conservação de momento do sistema. O momento se conserva já que se trata de uma colisão.(:
Antes da colisão, a bala tinha velocidade e o bloco tinha velocidade nula, logo, o momento inicial é:
Após a colisão, tanto o bloco quanto a bala se deslocam com a mesma velocidade
Como :
E essa é a velocidade do bloco logo após a colisão!
Resposta
a)
Demonstração.
b)
Exercício Resolvido #3
Uma cadeia linear de blocos de massa , ligadas com molas de constante elástica e massa desprezível, precisa de quantas condições iniciais para a completa descrição do sistema?
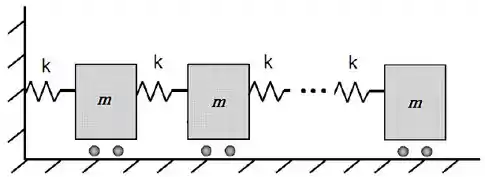
Considere apenas deslocamentos longitudinais.
Passo 1
Bom galera, pra resolver a equação de um MHS do tipo:
Nós precisamos geralmente de duas condições:
Uma velocidade inicial e um espaço inicial, certo?
Assim a gente consegue descrever completamente o sistema.
Agora, um sistema composto por molas, é um sistema complexo formado por MHS, ou seja, quantas condições vamos precisar ter pra descrever todo o sistema?
A resposta é . Duas condições para cada MHS.
Resposta
e)
Exercício Resolvido #4
Considere dois sistemas massa-mola conforme a figura abaixo. A razão entre a frequência natural do sistema 1 e a frequência natural do sistema 2 é:
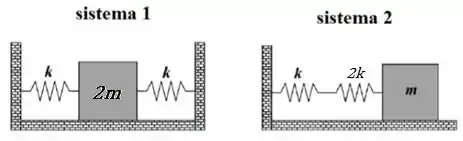
Passo 1
Vamos olhar primeiro o sistema .
Se deslocarmos o bloco para direita, por exemplo, a mola da direita irá empurrar o bloco com uma força e o bloco da esquerda irá puxar o bloco com uma força também (ambas as forças serão negativas porque estarão no sentido contrário a esse movimento ![]() ). Assim a força total será
). Assim a força total será
Que funciona como um sistema massa mola com uma constante de mola . Como a frequência é dada por
Passo 2
Agora vamos olhar para o sistema .
Pra esse sistema, nós temos uma associação bonitinha de molas em série tal como vimos na nossa teoria.
Aí ficou fácil! Sabemos que para molas associadas em série:
Assim,
De forma que a frequência nessa situação será dada por
Passo 3
Assim a razão fica
Resposta
Letra (D)
Exercício Resolvido #5
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 111-86-Modificado.
Uma mola uniforme com é cortada em dois pedaços, 1 e 2, cujos comprimentos no estado relaxado são e . Qual é o valor:
(a) de ?
(b) de ?
Um bloco preso na mola original oscila com uma frequência de . Qual é a frequência de oscilação se o bloco for preso:
(c) no pedaço 1?
(d) no pedaço 2?
Passo 1
Bom, como vimos na teoria, a constante vai ser inversamente proporcional ao comprimento da mola: a mais rígida será a mais curta, a menos rígida será a mais longa.
Passo 2
Assim:
a)
Observe que usamos , ou seja, o comprimento total da mola é a soma das duas partes cortadas.
Sacou? (:
Passo 3
b)
Vamos seguir o mesmo raciocínio:
Show?
Passo 4
c)
Beleza, aqui o enunciado te deu duas informações: a frequência de oscilação e a constante da mola original. Com isso, podemos determinar a massa do bloco e depois aplicar a equação pro pedaço de mola que o item (c) menciona.
A frequência da mola original vale:
Assim, usando a relação:
Achamos a massa!!!
Agora vamos imaginar que esse bloco, com essa massa, esteja oscilando com a mola de comprimento Só a gente reaplicar a equação:
A frequência de oscilação é dada por:
Passo 5
d)
Bom, agora é só fazer a mesma coisa com o pedaço 2:
A frequência de oscilação é dada por:
Resposta
a)
b)
c)
d)