Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Vetor de Poynting e Intensidade

Ver Todos os Exercícios

Teoria

Seja bem vindo ao RespondeAí! Você veio ao lugar certo pra aprender sobre o Vetor de Poynting!

O vetor de Poynting,  , serve para representar a densidade direcional do fluxo de energia eletromagnética no espaço.

Mas lendo assim isso não parece significar muita coisa né? Calma! Segura na minha mão que o RespondeAí! vai te ajudar nessa saga!

Vamos começar imaginando uma onda eletromagnética percorrendo o espaço!

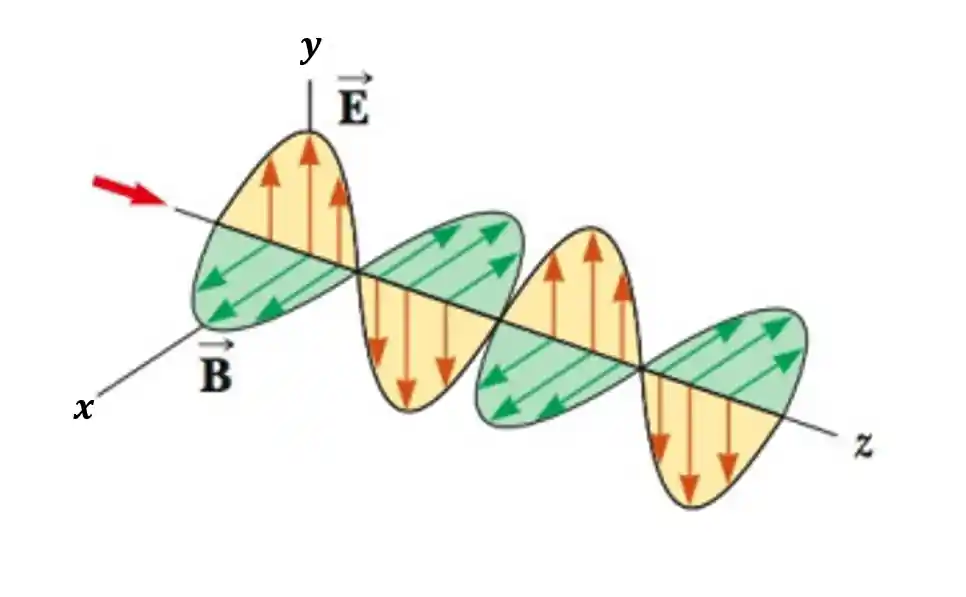
Representação de uma onda eletromagnética.
Representação de uma onda eletromagnética.

A onda eletromagnética transporta uma quantidade de energia e quantidade de energia transportada por área é o fluxo de energia, inclusive sua unidade é .

Então a gente precisa olhar pra a área onde essa onda eletromagnética passa.

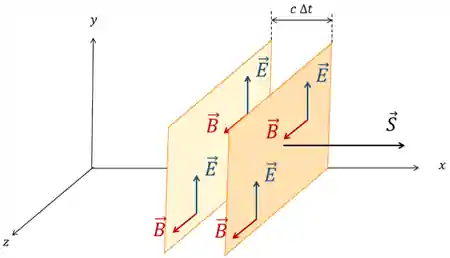
Onda eletromagnética percorrendo uma área.
Onda eletromagnética percorrendo uma área.

Na figura acima temos uma onda eletromagnética percorrendo uma área . Após um tempo ela percorre uma distância, que é dada pelo produto da velocidade da luz com o tempo .

Usando a densidade de energia transportada por uma onda eletromagnética, podemos dizer que a energia em uma região com volume  é:

Quando a onda eletromagnética atravessa uma área , ela transfere uma energia (variação da energia). Podemos dizer que isso é igual a variação de volume que a luz atravessa vezes a densidade de energia:

Esse é o fluxo de energia médio. Fazendo o tempo tender a zero, o fluxo de energia é:

Assim, chegamos a magnitude do vetor de Poynting ! Que é a energia, por unidade de tempo, por unidade de área. Ou potência por unidade de área para ficar mais agradável!

Podemos utilizar as relações que falamos anteriormente para acharmos outras formas de escrevermos Poynting, como:

Mas afinal, ainda não temos um vetor!

Como a onda se propaga no sentido de , o vetor de Poynting vai ter esse sentido, beleza?

 e  são perpendiculares, , Então esse produto vetorial tem exatamente o módulo que queremos, logo podemos escrever Vetor de Poynting   como:

Esse vetor é muito importante porque ele tem dentro dele a direção, o sentido e a magnitude do fluxo de energia transportada!

Intensidade de radiação

Como os campos elétrico  e magnético variam com o tempo em qualquer posição, o vetor de Poynting  também varia da mesma forma. E como essas frequências geralmente são muito altas, é mais simples trabalharmos com o valor médio do vetor de Poynting no tempo.

E é justamente esse valor médio do vetor de Poynting que chamamos de intensidade de radiação eletromagnética, ou intensidade da onda, dado por:

éáá

O fator  vem do fato de que o é  é a média temporal do vetor de Poynting e na conta aparece uma média temporal de  que dá .

Podemos utilizar o fato de que  para encontrar outras formas de escrever a equação.

áá

Podemos escrever em função de , é só lembrar que:

Aí as expressões ficam:

áá

Potência da Luz

Para sabermos a potência da luz em uma dada área, nós vemos quanta energia atravessou perpendicular à superfície.

Lembrando que, o fluxo é a potência (energia por tempo) da luz por unidade de área! E o fluxo de energia transportado pela luz é dado pelo vetor de Poynting..

A potência  que atravessa a superfície é o fluxo perpendicular ( ) multiplicado pela área.

Isso é o produto escalar entre o fluxo e o “vetor Área” (vetor normal à superfície e cujo módulo é a área). Mas e no caso da nossa esfera?

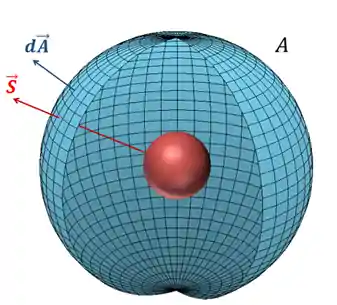
Esfera com área A.
Esfera com área A.

A gente divide ela em pequenas áreas.

E integramos todas:

CURIOSIDADE! Os painéis de energia solar são inclinados de forma a ficarem perpendiculares ao vetor de Poynting justamente para maximizar a potência que vem da energia solar. O  faz com que em outros ângulos a potência seja sempre menor!

A Intensidade da radiação varia com a área

Em exercícios e provas, em geral o vetor de Poynting vai ser sempre paralelo ao “vetor área”. Isso faz com que não precisemos nos preocupar com o ângulo  entre eles.

Se considerarmos, além disso, o fluxo médio na nossa integral, temos:

éé

Onde  é a área total da superfície e  é a potência da luz. Pela definição, é  é a intensidade! A intensidade ao longo da nossa área é:

No caso de uma superfície esférica, nós recaímos na nossa lâmpada de LED! 💡

Com  sendo a distância que a luz percorreu.

Em exercícios e provas, essa fórmula final é a mais importante!

Ficou com alguma dúvida?! Clica abaixo para ver nosso conteúdo em vídeo também!

Agora, vamos pros exercícios fixar as ideias!

Intensidade de radiação

Potência da Luz

A Intensidade da radiação varia com a área

Exercícios Resolvidos

Exercício Resolvido #1

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 29-10

Em uma onda de rádio plana o valor máximo do campo elétrico é 5,00   V / m .

Calcule:

  1. O valor máximo do campo magnético.
  2. A intensidade da onda.

Passo 1

Letra a)

O valor máximo do campo magnético é a sua amplitude.

Com a amplitude do campo elétrico, podemos encontrar a de B → a partir da equação:

E = c B

Temos pelo enunciado que E = 5,00   V / m e sabemos que a velocidade da luz é de c ≅ 3 ∙ 10 8   m / s .

B m á x = E m á x c = 5 3 ∙ 10 8 ≅ 1,67 ∙ 10 - 8 T

Passo 2

Letra b)

Sabemos que a intensidade da onda é o fluxo médio. Assim:

I = S m é d = E m 2 2 μ 0 c = 5 2 2 ∙ 4 π ∙ 10 - 7 ∙ ( 3 ∙ 10 8 ) ≅ 3,31 ∙ 10 - 2 W / m 2

Resposta

Letra a)

B m á x ≅ 1,67 ∙ 10 - 8 T

Letra b)

I ≅ 3,31 ∙ 10 - 2 W / m 2

Exercício Resolvido #2

UFRJ, Física 4, Prova 1, 2011.2

Uma onda eletromagnética plana tem o vetor campo magnético dado por

B → = 4 π cos ⁡ π 2 z - 1,5 π × 10 8 t x ^ - 4 π sen ⁡ π 2 z - 1,5 π × 10 8 t y ^   T ;

  1. Determine: a direção e sentido de propagação da onda.
  2. Determine o vetor campo elétrico associado a esta onda.
  3. Calcule o vetor de Poynting.
  4. Calcule a intensidade da onda.

Passo 1

Letra a)

O problema nos pede para descobrir a direção e sentido de propagação da onda.

Esta questão é diferente das outras pelo fato do campo magnético B → ter componentes em duas direções.

Mas fica tranquilo, não é um bicho de 7 cabeças! Vamos seguir o mesmo raciocínio de antes.

Vamos analisar o argumento das funções senoidais

π 2 z - ω t

Para que o argumento permaneça constante, conforme o tempo t aumenta, é necessário que o valor de z também aumente.

Logo, a onda se propaga no sentido do vetor + z ^ .

Passo 2

Letra b)

O problema nos pede para calcular o vetor de campo elétrico E → .

Sabemos que E → é perpendicular a B →

O vetor possui B → possui duas componentes, nos sentidos x ^ e ( - y ^ ) .

Então vamos fazer o seguinte, vamos dividir esse problema em duas partes, trabalhando como cada componente separadamente, ok?

B x → = 4 π cos ⁡ π 2 z - 1,5 π × 10 8 t x ^ T ; ( i )

B y → = - 4 π sen ⁡ π 2 z - 1,5 π × 10 8 t y ^   T ; ( i i )

Passo 3

( i )

B x → = 4 π cos ⁡ π 2 z - 1,5 π × 10 8 t x ^ T ;

Sabemos que a onda se propaga no sentido + z ^ , então temos que encontrar o componente E 1 → tal que o produto vetorial E → 1 × B → x tenha o resultado no sentido + z ^ .

Sabemos também que E → 1 é perpendicular a B → x e a z ^ . Assim, E → 1 só pode estar no eixo y .

Usando a regra da mão direita descobrimos que E → 1 tem o sentido do vetor - y ^ .

- y ^ × x ^ = z ^

Para determinar o módulo de E → 1 , basta usar a relação:

E 1 = c B x

Onde c = 3,0 × 10 8   m / s . Logo:

E 1 = 3,0 × 10 8 × 4 π cos ⁡ π 2 z - 1,5 π × 10 8 t

E 1 = 12 π × 10 8 cos ⁡ π 2 z - 1,5 π × 10 8 t

Por fim:

E → 1 = - 12 π × 10 8 cos ⁡ π 2 z - 1,5 π × 10 8 t y ^

Passo 4

i i B y → = - 4 π sen ⁡ π 2 z - 1,5 π × 10 8 t y ^   T

O raciocínio é o mesmo do caso anterior.

Agora, E → 2 é perpendicular a B → y e a z ^ . Portanto, E → 2 só pode estar no eixo x .

Usando a regra da mão direita descobrimos que E → 2 tem o sentido do vetor - x ^ .

- x ^ × - y ^ = z ^

Para determinar o módulo de E → 2 , basta usar a relação:

E 2 = c B y

Onde c = 3,0 × 10 8   m / s . Logo:

E 2 = 3,0 × 10 8 × 4 π sen ⁡ π 2 z - 1,5 π × 10 8 t

E 2 = 12 π × 10 8 sen ⁡ π 2 z - 1,5 π × 10 8 t

Por fim:

E → 2 = 12 π × 10 8 sen ⁡ π 2 z - 1,5 π × 10 8 t x ^

Logo:

E → = E → 1 + E → 2

E → = - 12 π × 10 8 sen ⁡ π 2 z - 1,5 π × 10 8 t x ^ - 12 π × 10 8 cos ⁡ π 2 z - 1,5 π × 10 8 t y ^

Passo 5

Letra c)

O problema nos pede para calcular o vetro de Poynting S → .

O vetor de Poynting S → é dado por

S → = E → × B → μ 0

Onde:

E → = - 12 π × 10 8 sen ⁡ π 2 z - 1,5 π × 10 8 t x ^ - 12 π × 10 8 cos ⁡ π 2 z - 1,5 π × 10 8 t y ^ V m ;

B → = 4 π cos ⁡ π 2 z - 1,5 π × 10 8 t x ^ - 4 π sen ⁡ π 2 z - 1,5 π × 10 8 t y ^   T ;

μ 0 = 4 π × 10 - 7 N / A 2 ;

E → × B → = 48 π 2 × 10 8 sen 2 ⁡ π 2 z - 1,5 π × 10 8 t + 48 π 2 × 10 8 cos 2 ⁡ π 2 z - 1,5 π × 10 8 t z ^ ;

E → × B → = 48 π 2 × 10 8 z ^ ;

Logo:

S → = 48 π 2 × 10 8 4 π × 10 - 7   z ^

S → = 1,2   π × 10 16   z ^         W / m 2

Passo 6

Letra d)

O problema nos pede para descobrir a intensidade I da onda.

Quando estudamos o vetor de Poynting, vimos que

I = S médio

Mas como o módulo do vetor de Poynting, neste caso, não varia com o tempo, podemos dizer que

I = S = 1,2   π × 10 16       W / m 2

Resposta

Letra a)

A onda se propaga no sentido do vetor + z ^ .

Letra b)

E → = - 12 π × 10 8 sen ⁡ π 2 z - 1,5 π × 10 8 t x ^ - 12 π × 10 8 cos ⁡ π 2 z - 1,5 π × 10 8 t y ^

Letra c)

S → = 1,2   π × 10 16   z ^         W / m 2

Letra d)

I = 1,2   π × 10 16       W / m 2

Exercício Resolvido #3

UFRJ, Física 4, Prova 1, 2008.2

Uma onda eletromagnética monocromática plana possui um campo magnético dado por

B → x , t = B 0 y j ^ sen ⁡ ( ω t + k x ) + B 0 z k ^ sen ⁡ ( ω t + k x )

  1. Escreva as equações vetoriais para E → e S → .
  2. Calcule a intensidade da onda no ponto P = 1,2 , 0 .

Passo 1

Letra (a): Escreva as equações vetoriais para E → e S → .

Para começar, temos que descobrir o sentido em que a onda está se deslocando e, para isso, analisaremos o argumento da função senoidal

ω t + k x

Para que o argumento permaneça constante, conforme o valor do tempo t aumenta, é necessário que o valor de x diminua. Assim, a onda eletromagnética se propaga no sentido do vetor - i ^ .

Passo 2

Sabendo que a onda se propaga no sentido do vetor - i ^ e que E → e B → são perpendiculares, temos que:

B → = 1 c ( - i ^ × E → )

B 0 y j ^ + B 0 z k ^ = 1 c i ^ j ^ k ^ - 1 0 0 0 E 0 y E 0 z = E 0 z c j ^ - E 0 y c k ^

E 0 y = - c B 0 z

E 0 z = c B 0 y

Logo:

E → x , t = - c B 0 z j ^ sen ⁡ ω t + k x + c B 0 y k ^ sen ⁡ ( ω t + k x )

Passo 3

S → x , t = E → × B → μ 0

S → x , t = 1 μ 0 i ^ j ^ k ^ 0 - c B 0 z c B 0 y 0 B 0 y B 0 z sen 2 ⁡ ( ω t + k x )

S → x , t = - B 0 z 2 + B 0 y 2 c μ 0 i ^ sen 2 ⁡ ( ω t + k x )

S → x , t = - B 0 2 c μ 0 i ^ sen 2 ⁡ ( ω t + k x )

Passo 4

Letra (b): Calcule a intensidade da onda no ponto P = 1,2 , 0 .

A intensidade é igual ao valor médio do vetor de Poynting, logo:

I = S - = B 0 2 c 2 μ 0

Logo, a intensidade independe da posição.

Resposta

Letra (a):

E → x , t = - c B 0 z j ^ sen ⁡ ω t + k x + c B 0 y k ^ sen ⁡ ( ω t + k x )

S → x , t = - B 0 2 c μ 0 i ^ sen 2 ⁡ ( ω t + k x )

Letra (b):

I = B 0 2 c 2 μ 0

Exercício Resolvido #4

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 30-30

A intensidade I da luz emitida por uma fonte pontual e isotrópica é medida em função da distância r da fonte. A Fig. 33-40 mostra a intensidade I em função do inverso do quadrado da distância, r - 2 .

A escala do eixo vertical é definida por I s = 200   W / m 2 , e a escala do eixo horizontal é definida por r s - 2 = 8,0   m - 2 .

Qual é a potência da fonte?

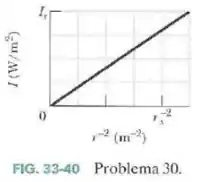
Passo 1

Primeiramente, precisamos compreender o que significa esse gráfico.

Vamos começar pela relação que sabemos ter a intensidade e a potência. Dessa vez, vamos começar já considerando todas as aproximações necessárias que nos dá:

I = P A

Como a fonte é pontual e isotrópica, podemos dizer que a luz se espalha em superfícies esféricas ao redor dela. Podemos então substituir a área da esfera:

I = P 4 π r 2 = P 4 π   r - 2

Eu reescrevi a fórmula de forma a facilitar um insight. Se considerarmos que a intensidade varia linearmente com r - 2 , então o gráfico é dado por:

I = α r - 2

Comparando essa equação com a de cima, temos:

α = P 4 π

Ou seja, a potência dividida por 4 π é o coeficiente angular da reta apresentada no gráfico.

Passo 2

Agora, para achar a potência, nós calculamos o coeficiente angular da reta e multiplicamos por 4 π .

P = 4 π α

Pela escala do enunciado, r s - 2 = 8,0   m - 2 corresponde a 4 unidades do eixo horizontal (4 quadradinhos). Logo, cada unidade é dada por u = 2,0   m - 2 .

Com isso, o último ponto apresentado no gráfico corresponde a r - 2 = 10,0   m - 2 , que corresponde à intensidade I = I s = 200   W / m 2 .

Usando esse ponto, o coeficiente angular vai ser:

α = 200 - 0 10 - 0 = 200 10 = 20   W

Assim, a potência será de

P = 4 π ∙ 20 ≅ 251,33   W

Resposta

A potência da fonte é de P ≅ 251,33   W .

Exercício Resolvido #5

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 29-17

Um avião que se encontra a uma distância de 10   k m de um transmissor de rádio recebe um sinal com uma intensidade de 10   μ W / m 2 .

Determine a amplitude:

  1. Do campo elétrico associado ao sinal na posição do avião.
  2. Do campo magnético associado ao sinal na posição do avião.
  3. Se o transmissor irradia uniformemente ao longo de um hemisfério, qual é a potência da transmissão?

Passo 1

Letra a)

Para calcular o campo elétrico associado ao sinal, podemos usar a Intensidade do mesmo. A intensidade é dada por:

I = 1 2 E m á x B m á x μ 0

Mas como E = c B , podemos reescrever:

I = 1 2 E m á x 2 μ 0 c

E m á x = 2 I ∙ μ 0 ∙ c

μ 0 é a permeabilidade magnética no vácuo, e vale 4 π ∙ 10 - 7 N / A 2 , c é a velocidade da luz 3 ∙ 10 8   m / s e I é a intensidade dada no enunciado 10   μ W / m 2 = 10 ∙ 10 - 6 W / m 2 .

E m á x = 2 ∙ ( 10 ∙ 10 - 6 ) ∙ 4 π ∙ 10 - 7 ∙ 3 ∙ 10 8 ≅ 86,83 ∙ 10 - 3 V / m = 8,683 ∙ 10 - 2 V / m  

Passo 2

Letra b)

Tem duas formas de calcular o campo magnético. Uma é aproveitando a nossa resposta da letra (a), e usando a relação E = c B . A outra, é fazendo exatamente o que fizemos antes, mas escrevendo a intensidade como função do campo magnético.

Vamos seguir a segunda forma.

Já sabemos a fórmula da intensidade (tem na letra anterior), e agora usando a nossa relação mágica E = c B , teremos:

I = 1 2 c B m á x 2 μ 0

B m á x = 2 I ∙ μ 0 c

Novamente, μ 0 é a permeabilidade magnética no vácuo, e vale 4 π ∙ 10 - 7 N / A 2 , c é a velocidade da luz 3 ∙ 10 8   m / s e I é a intensidade dada no enunciado 10   μ W / m 2 = 10 ∙ 10 - 6 W / m 2 .

B m á x = 2 ∙ ( 10 ∙ 10 - 6 ) ∙ 4 π ∙ 10 - 7 3 ∙ 10 8 ≅ 28,94 ∙ 10 - 11 T = 2,894 ∙ 10 - 10 T

Passo 3

Letra c)

Sabemos que a intensidade da luz varia com a área na qual a luz se espalha. Assim, indo do início, a potência é:

P = ∮ S → ∙ d A →

Considerando o fluxo sempre paralelo ao vetor normal da área, e usando o fluxo médio (intensidade):

P = S m é d ∮ d A = I ∙ ∮ d A

P = I ∙ A

O enunciado nos diz que o sinal é irradiado ao longo de um hemisfério, ou seja, metade de uma esfera. A área da esfera é:

A e s f = 4 π r 2

Logo, a do hemisfério será metade disso:

A h e m i s f = 2 π r 2

A potência será

P = I ∙ 2 π r 2

A distância da fonte ao nosso avião é de 10   k m , o que nos diz que estamos considerando que a luz se espalhou por um hemisfério com um raio de 10   k m = 10 ∙ 10 3 m .

A intensidade também é dita no enunciado, I = 10   μ W / m 2 = 10 ∙ 10 - 6   W / m 2

P = 10 ∙ 10 - 6 ∙ ( 2 π ∙ 10 ∙ 10 3 2 )

P = 10 - 5 ∙ 2 π ∙ 10 8

P ≅ 6 , 28 ∙ 10 3   W

Resposta

Letra a)

E m á x ≅ 8,683 ∙ 10 - 2 V / m

Letra b)

B m á x ≅ 2,894 ∙ 10 - 10 T

Letra c)

P ≅ 6,28 ∙ 10 3   W

Exercício Resolvido #6

Young e Freedman, Física III Eletromagnetismo, 12ª ed, São Paulo: Addison Wesley, 2009, pp 400-32.15

Podemos modelar de forma razoável uma lâmpada incandescente de 75   W como uma esfera de 6,0   cm de diâmetro.

Tipicamente, somente cerca de 5% da energia vai para a luz visível; o restante vai, em grande parte, para a radiação infravermelha não visível.

  1. Qual é a intensidade da luz visível (em W / m 2 ) na superfície da lâmpada?
  2. Quais são as amplitudes dos campos elétrico e magnético nessa superfície, para uma onda senoidal com essa intensidade?

Passo 1

Letra a)

O problema nos dá a potência da lâmpada P , o diâmetro da esfera d e nos pede para calcular a intensidade da luz visível na superfície da lâmpada.

Sabemos que a intensidade I luz pode ser calculada a partir das seguintes equações:

I = S médio = E máx B máx 2 μ 0

Assim, se descobrirmos o módulo do vetor de Poynting podemos encontrar a intensidade.

Passo 2

Encontrando o valor de S médio .

Com os dados que o problema nos dá ( P e d ), podemos encontrar o valor de S médio a partir da seguinte equação

P = ∮ S → ∙ d A →

Onde P é a potência e d A → é o elemento de área.

Como S →   e   d A → são paralelos em qualquer ponto da esfera.

P = S médio ∙ ∮ d A = S médio ∙ A

S médio = P A

Onde:

d = 6   cm = 0,06   m ;

A = 4 π r 2 = 4 π d 2 4 = π d 2 = 0,0113   m 2 ;

P = 75   W ;

Logo:

I = S médio = 75 0,0113 = 6.631,45   W / m 2

Passo 3

No entanto, o problema nos diz que somente cerca de 5% da energia da lâmpada vai para a luz visível. Logo:

I luz = 5 %   I ≅ 331,57   W / m 2

Passo 4

Letra b)

Podemos relacionar a intensidade I luz o módulo do vetor de Poynting S com as amplitudes dos campos elétrico e magnético através da seguinte equação:

I luz = S = E máx B máx 2 μ 0

E a partir da relação E = c B , nós podemos encontrar outras relações, como:

I luz = E máx 2 2 μ 0 c = c B máx 2 2 μ 0

Agora ficou tranquilo. Vamos começar pelo campo elétrico:

E máx = 2 I luz ∙ μ 0 ∙ c

Onde:

I luz = 331,57   W / m 2 ;

μ 0 = 4 π × 10 - 7   N / A 2 ;

c = 3 × 10 8   m / s ;

Logo:

E máx = 2 × 331,57 × 4 π × 10 - 7 × 3 × 10 8

E máx = 500   V / m

Como já sabemos, E = c B , logo:

B máx = E máx c ≅ 1,7 × 10 - 6   T

B máx ≅ 1,7   μT

Resposta

Letra a)

I luz ≅ 331,57   W / m 2

Letra b)

E máx = 500   V / m

B máx ≅ 1,7   μT

Exercício Resolvido #7

UFRJ, Física 4, Prova 1, 2009.1, modificado

O vetor de Poynting associado com uma onda eletromagnética harmônica que se propaga no vácuo é dado por:

S → z , t = 100 4 π cos 2 ⁡ 10 z - 3 × 10 9   t   z ^

E é medido em W / m 2 .

  1. Qual a direção e o sentido de propagação da onda? Justifique a sua resposta.
  2. Suponha que em t = 0 e no plano z = 0 o campo elétrico aponte no sentido do eixo O x . Determine a expressão vetorial do campo elétrico associado a este vetor de Poynting.
  3. Determine o vetor campo magnético associado com este vetor de Poynting.
  4. Calcule o comprimento de onda e a frequência desta onda harmônica.

Passo 1

Letra (a)

Beleza!

Temos duas formas de mostrar a direção e sentido de propagação e justificar, vou te falar em ordem de preferência.

1º modo: Analisando o vetor

O vetor de Poynting sempre tem a direção e sentido de propagação da onda! Isso ocorre para qualquer valor de z ou de t .

Vamos dar uma olhada na equação:

S → z , t = 100 4 π cos 2 ⁡ 10 z - 3 × 10 9   t   z ^

Assim, a onda se propaga no sentido + z ^ .

Passo 2

2º modo: Analisando o argumento dentro da função senoidal

A análise que eu vou te mostrar agora te ajuda tanto quando o problema te dá o vetor de Poynting, quanto quando ele te dá o campo magnético ou o vetor de campo elétrico.

Vamos dar uma olhada na equação que o problema nos dá:

S → z , t = 100 4 π cos 2 ⁡ 10 z - 3 × 10 9   t   z ^

Agora, o que vamos analisar é o argumento que está dentro da função senoidal, nesse caso será

cos 2 ⁡ 10 z - 3 × 10 9   t

O que você precisa ter em mente pra descobrir a direção e o sentido de propagação da onda é que, para o argumento

10 z - 3 × 10 9   t

ser constante, é necessário que, conforme o tempo aumente, o valor de z também aumente.

Assim, a onda se propaga no sentido + z ^ .

A lógica é a mesma para qualquer outra variável, você só deve repetir o pensamento, por exemplo, se o argumento fosse

10 z + 3 × 10 9   t

Para que ele permanecesse constante, conforme o tempo aumentasse, o valor de z deveria diminuir. Logo, a onda se propagaria no sentido - z ^ .

Entendeu?

Passo 3

Letra (b)

Podemos associar o módulo do vetor de Poynting S com o módulo do campo elétrico E por:

S = ϵ 0 c E 2 → E = S ϵ 0 c

Onde:

S → z , t = ( 100 / 4 π ) cos 2 ⁡ 10 z - 3 × 10 9   t   z ^ ;

c = 3 × 10 8   m/s ;

ϵ 0 = 8,85 × 10 - 12   F/m ;

Logo:

E = ( 100 / 4 π ) cos 2 ⁡ 10 z - 3 × 10 9   t 8,85 × 10 - 12 × 3 × 10 8

E z , t = 54,75   cos ⁡ ( 10 z - 3 × 10 9 t )       V/m

Passo 4

O problema nos diz que quando t = 0 e z = 0 , o campo elétrico aponta no sentido + x ^ .

E 0,0 = 54,75     V/m

Logo:

E → z , t = 54,75 cos ⁡ ( 10 z - 3 × 10 9 t ) x ^       V/m

Passo 5

Letra (c)

Sabemos que o campo elétrico E e o campo magnético B estão relacionados por:

E = c B → B = E c

Onde:

E z , t = 54,75 cos ⁡ ( 10 z - 3 × 10 9 t ) V/m ;

c = 3 × 10 8   m/s ;

Logo:

B = 54,75 3 × 10 8 cos ⁡ ( 10 z - 3 × 10 9 t )

B = 18,25 × 10 - 8 cos ⁡ 10 z - 3 × 10 9 t   T

Passo 6

Agora precisamos descobrir a direção e sentido do campo magnético.

O produto vetorial E → × B → nos dá a direção e o sentido de propagação da onda.

Sabemos que a onda se propaga no sentido do vetor + z ^ e que o campo elétrico se propaga no sentido do vetor + x ^ .

Assim, usando a regra da mão direita, com o dedo indicador representando o campo elétrico e o polegar representando o sentido de propagação da onda, o dedo médio vai te dar a direção e sentido do campo magnético.

Então, de acordo com a regra da mão direita, o campo magnético tem o sentido do vetor + y ^ .

B → z , t = 18,25 × 10 - 8 cos ⁡ 10 z - 3 × 10 9 t y ^       T

Passo 7

Letra (d)

Analisando a equação do campo elétrico:

E → z , t = 54,75 cos ⁡ ( 10 z - 3 × 10 9 t ) x ^       V/m

Temos que:

ω = 3 × 10 9   rad/s ;

k = 10   rad/m ;

Encontrando a frequência:

ω = 2 π f → f = ω 2 π

f = 3 × 10 9 2 π = 4,77 × 10 8   Hz

Encontrando o comprimento de onda:

k = 2 π λ → λ = 2 π k

λ = 2 π 10 = 0,63   m

Resposta

Letra (a):

A onda se propaga no sentido + z ^ .

Letra (b):

E → z , t = 54,75 cos ⁡ ( 10 z - 3 × 10 9 t ) x ^         V/m

Letra (c):

B → z , t = 18,25 × 10 - 8 cos ⁡ 10 z - 3 × 10 9 t y ^         T

Letra (d):

f = 4,77 × 10 8   Hz

λ = 0,63   m

Exercício Resolvido #8

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 29-14

Frank D. Drake, um investigador do programa SETI (Search for Extra-Terrestrial Intelligence, ou seja, Busca de Inteligência Extraterrestre), disse uma vez que o grande radiotelescópio de Arecibo, em Porto Rico (Fig. 33-38), “é capaz de detectar um sinal que deposite em toda a superfície da Terra uma potência de apenas um picowatt”.

  1. Qual é a potência que a antena do radiotelescópio de Arecibo receberia de um sinal como esse? O diâmetro da antena é 300   m .
  2. Qual teria que ser a potência de uma fonte isotrópica situada no centro de nossa galáxia para que um sinal com essa potência chegasse à Terra?

O centro da galáxia fica a 2,2 × 10 4   anos-luz de distância. Um ano-luz é a distância que a luz percorre em um ano.

O raio médio da Terra é de 6,37 × 10 6   m .

Passo 1

Letra a)

Na fala do Frank D. Drake, ele menciona a potência do sinal espalhado ao redor da terra que poderia ser recebido.

Assim, a intensidade em cada ponto da Terra seria:

I = P A = P 4 π R 2

Onde R = 6,37 × 10 6   m é o raio da Terra e P = 1   p W = 10 - 12   W é a potência do sinal.

I r e c = 10 - 12 4 π ∙ 6,37 ∙ 10 6 2

Passo 2

Com o passo anterior, encontramos a intensidade que a antena de Arecibo recebe. Porém, o que queremos é a potência recebida.

I r e c = P r e c A a n t e n a

P r e c = I r e c ∙ A a n t e n a

Agora, tem algo importante a comentarmos:

Essa imagem é uma foto da antena de Arecibo. Se você olhar bem, ela tem um formato circular, parecendo uma panqueca gigante. Isso significa que a sua área vai ser a área de um círculo.

A c i r c u l o = π r 2 = π d 2 4

Onde d = 2 r é o diâmetro da antena que pelo enunciado tem um tamanho de 300   m . Isso nos dá:

A c i r c u l o = π ∙ 300 2 4

Substituindo a intensidade recebida que vimos no passo anterior, e a área do círculo:

P r e c = 10 - 12 4 π ∙ 6,37 ∙ 10 6 2 ∙ π ∙ 300 2 4

P r e c ≅ 138,63 ∙ 10 - 24   W = 1,3863 ∙ 10 - 10   p W

Passo 3

Letra b)

Sabemos a intensidade recebida em cada ponto da Terra pela letra (a).

Queremos então saber qual potência seria necessária no centro da galáxia para que de fato o sinal eletromagnético chegasse aqui com essa intensidade. Usando nossa fórmula:

I r e c = P c e n t r o A

P c e n t r o = I r e c ∙ A

Onde I r e c é aquele calculado no passo 1.

Considerando a fonte pontual isotrópica no centro da galáxia, ela emite luz em formato de superfícies esféricas. Assim, a área que a luz se espalha é:

A = 4 π D 2

Onde D = 2,2 × 10 4 anos-luz é a distância do centro da galáxia até a terra. Contudo, queremos converter essa unidade para algo melhor de calcular, de preferência “metros”.

A luz viaja a uma velocidade de 3 ∙ 10 8   m / s . Agora, precisamos saber quantos segundos tem em um ano. Um ano tem 365   d i a s , um dia tem 24   h o r a s , uma hora tem 60   m i n u t o s e um minuto tem 60   s e g u n d o s . Assim:

1   A n o = 365 ∙ 24 ∙ 60 ∙ 60 = 31   536   000   s e g u n d o s

Logo, em um ano, a luz percorre uma distância de

1   A n o - L u z =   3 ∙ 10 8 ∙ 31   536   000 = 9 , 4608 ∙ 10 15   m

Com isso, a distância do centro da galáxia até aqui fica

D = 2,2 ∙ 10 4 ∙ ( 9,4608 ∙ 10 15 )

A área então que a luz se espalha ao vir do centro da galáxia até a Terra é de

A = 4 π ∙ 9,4608 ∙ 10 15 ∙ 2,2 ∙ 10 4 2

Passo 4

A potência necessária no centro da galáxia é:

P c e n t r o = I r e c ∙ A

Vimos que:

A = 4 π ∙ 9,4608 ∙ 10 15 ∙ 2,2 ∙ 10 4 2

I r e c = 10 - 12 4 π ∙ 6,37 ∙ 10 6 2

Substituindo na nossa equação:

P c e n t r o = 10 - 12 4 π ∙ 6,37 ∙ 10 6 2 ∙ 4 π ∙ 9,4608 ∙ 10 15 ∙ 2,2 ∙ 10 4 2 ≅ 10,676 ∙ 10 14   W

Resposta

Letra a)

A potência que a antena receberia de um sinal como esse é de P r e c ≅ 1 , 3863 ∙ 10 - 2 2   W

Letra b)

A potência necessária no centro da galáxia seria de P c e n t r o ≅ 1 , 0676 ∙ 10 1 5   W

Exercícios de Livros Relacionados

Demonstre, a partir das eqs. de Maxwell incluindo uma corrente j → , a expressão do balanço de energia médio para um campo monocromático, - div ⁡ S → + = 1 2 j → * ∙ E → + 2 i ω U E - U M Onde S → + é
Alguns escritores de ficção - cientifica têm descrito que velas solares poderiam propulsionar naves interestelares. Imagine uma vela gigante em uma nave espacial sujeita à pressão de radiação de nosso
Uma onda eletromagnetica tem frequencia de 100 MHz e esta viajando no vacuo.O campo magnetico edado por B(2,t)=（1,00x10-*T)cos(k-wf)i.(a)Determine o comprimento de onda e a direcao de propagacao desta
Os campos eletricos de duas ondas harmonicas eletromagneticas de frequencias angulares a e w,sao dados por E;=E:o cos(k,x-of)j e por E:=Ea cos(k,x-wt+8)j.Para a resultante destas duas ondas,determine(
Um longo solenoide com n voltas por unidade de comprimento conduz uma corrente que aumenta linearmente com o tempo. O solenoide tem raio R , comprimento L e a corrente I nas voltas é dada por I = a t