Interferência em Filmes Finos
Produzido por Bruno SoaresTeoria
Filmes Finos
Agora sim, depois de por uma árdua jornada passar, pronto para entender um caso específico você está: a bolha de sabão!!!

A bolha de sabão é um exemplo do que chamamos de filmes finos.
Interferência na bolha de sabão
Vamos avaliar o porquê de vermos uma figura de interferência na bolha.
A bolha é um filme bem fininho de sabão com ar de ambos os lados. Quando um raio de luz entra perpendicular na bolha de sabão, parte dele reflete na bolha, e parte refrata, se propagando através dela.
A parte refratada também reflete! Só que dessa vez, do outro lado do filme. E como o filme é fino, os dois raios conseguem se manter coerentes. A imagem abaixo está com uma ligeira inclinação no raio incidente, só pra ficar mais fácil de ver.
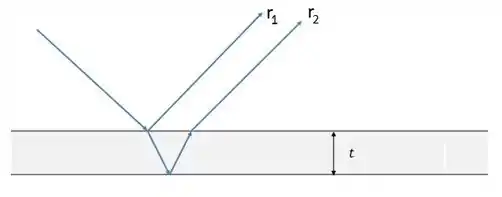
E é aí que a mágica acontece! O raio de luz sofreu uma mudança de fase em relação ao raio . Então, quando ele volta, os dois raios sofrem uma interferência que depende dessa mudança!
Vamos ver quais as mudanças de fase acontecem:
Diferença de caminho ótico
O raio acaba percorrendo um caminho maior que porque ele percorre duas vezes a espessura do filme (na ida e na volta). Como a espessura é a diferença é então . Assim, temos:
Lembrando que o comprimento de onda dentro do filme é .
Obs: Se o raio não entrar perpendicularmente, temos que corrigir a diferença de caminho ótico adicionando um cosseno do ângulo entre o raio de luz e a normal do filme, fazendo
Mudança de fase por reflexão
Quando a luz reflete de um meio com índice de refração menor em um meio com índice de refração maior, ela sofre uma mudança de fase! Essa mudança faz a onda ficar com a fase oposta, ou seja, é uma diferença de .
Se a luz reflete de um meio com índice de refração maior em um meio com índice de refração menor então ela não sofre nada
Fica mais fácil vendo esse esqueminha
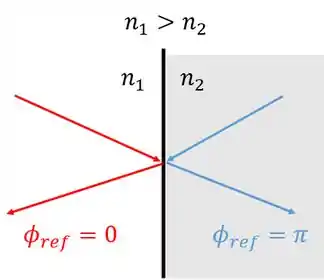
Uma analogia legal para lembrar-se disso é a de duas cordas presas uma na outra.
Quando a gente balança uma corda mais fina, no momento que o pulso passa para a corda mais grossa, parte é refletida com fase contrária.
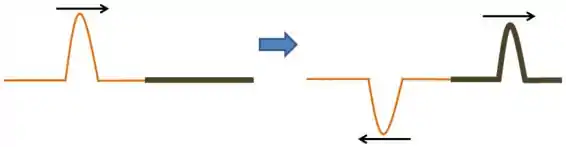
Quando a gente balança uma corda mais grossa, no momento que o pulso passa para a corda mais fina, parte é refletida com a mesma fase.

Interferência total
No final a nossa diferença de fase total vai ser a soma dessas duas:
Aí, quando você tiver calculado basta ver se a interferência vai ser construtiva ou destrutiva como antes ;)
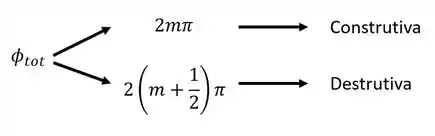
Dessa vez, valores negativos de não valem! A espessura e o índice de refração são positivos, então ser negativo não faria o menor sentido!!!
Filme fino cercado por dois meios diferentes
Quando colocamos película de Insufilm no carro, nós temos uma situação parecida com a da bolha de sabão: a luz passa por um filme fino. Porém, dessa vez, o filme não está entre duas camadas de ar, e sim entre ar e o vidro!

A situação vai ser essa aqui ó
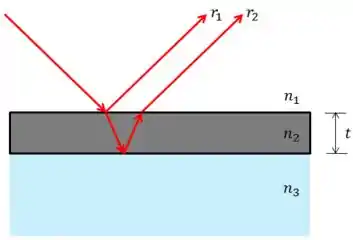
Agora, na hora de ver a diferença de fase no filme fino, temos que tomar muito cuidado se a reflexão do raio causa mudança de fase.
Porém, não é só isso! E se, na verdade, a luz tivesse vindo de um cristal, ao invés do ar? A reflexão de não teria mudança de fase!
Então agora, temos que nos preocupar com as duas reflexões! As regras são as seguintes:
- Se nenhum raio sofre mudança de fase de reflexão a mudança de fase entre eles é nula.
- Se somente um raio (não importa qual) sofre mudança de fase de reflexão a mudança de fase entre eles é .
- Se os dois raios sofrem mudança de fase de reflexão a mudança de fase entre eles é . .
Interferência na Transmissão em Filmes Finos
Quando você coloca insulfilme no carro, isso dificulta que pessoas de fora do carro enxerguem o que está acontecendo dentro do carro. Porém, a pessoa dentro do carro continua conseguindo enxergar o que acontece do lado de fora. Como explicar isso?
Uma película fina não apenas reflete a luz, mas ela também deixa passar luz.
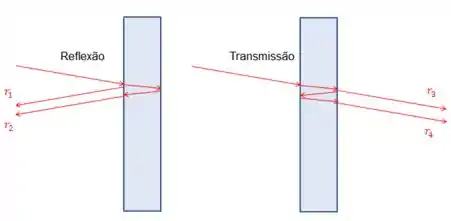
Muitos exercícios podem pedir não só quando que teremos uma interferência construtiva na reflexão, mas também quando teremos uma na transmissão da luz.
O conceito continua o mesmo: ver a diferença de fase pelas reflexões e pela diferença de caminho. Porém, com a transmissão, duas reflexões acontecem dentro do filme. O lance aqui então é prestar atenção em quais dessas reflexões internas vai ter mudança de fase.
A diferença de percurso entre e é a mesma que entre e . Já a diferença de fase por reflexão é diferente.
A primeira reflexão de é exatamente igual a reflexão de .
A segunda reflexão de é o exato oposto da reflexão de .
Intensidade resultante de filmes finos
Bem, sabemos que, caso não estejamos na Matrix, o mundo não é binário. Às vezes, podemos ver meio mal e porcamente o que acontece atrás do insulfilm do carro.
Nestes casos, a interferência não é nem totalmente construtiva nem totalmente destrutiva.
Mas, como saber o quão bem vamos enxergar através do filme? Calculando a sua intensidade!
Vamos ver novamente a imagem da interferência em filmes finos.
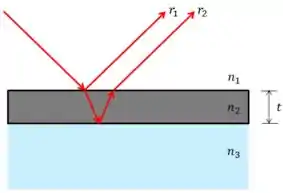
Neste caso, temos interferência entre dois raios luminosos, o raio e o raio . Show, porque tem uma fórmula que nos dá exatamente a intensidade resultante da interferência de dois raios!
Onde é a intensidade resultante, é a intensidade máxima que pode resultar ( que é quatro vezes a intensidade da luz incidente, ) e é a diferença de fase entre os dois raios.
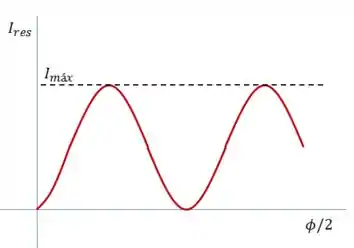
Agora, a diferença de fase vai depender dos meios que tem em torno do nosso filme fino.
E isso é tudo, amigos! Agora entre nas catacumbas dos exercícios, para pegar o tesouro sagrado: a nota 10.
Diferença de caminho ótico
Mudança de fase por reflexão
Interferência total
Filme fino cercado por dois meios diferentes
Interferência na Transmissão em Filmes Finos
Intensidade resultante de filmes finos
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 103-37.
Uma onda luminosa de comprimento de onda incide perpendicularmente em uma película de sabão (com ) suspensa no ar.
Quais são as duas menores espessuras do filme para as quais as ondas refletidas pelo filme sofrem interferência construtiva?
Passo 1
Vamos começar com a boa e velha condição para que haja interferência construtiva em um filme fino.
Onde é a espessura do filme.
Note que:
- Nós temos o valor de e o valor de , dados pelo enunciado.
- Quanto maior o valor de , maior o valor de . Logo, queremos os dois menores valores de :0 e 1.
Passo 2
Pelo enunciado, e . Além disso, como vimos antes, queremos e .
Substituindo:
Resposta
As duas menores espessuras do filme para ter interferência construtiva são aproximadamente e .
Exercício Resolvido #2
Física – Halliday – Volume 4 – Capítulo 35 – Seção 7 – Exercício 36
Uma película de sabão ) com de espessura é iluminada perpendicularmente com luz branca. Para quantos comprimentos de onda diferentes na faixa de a a luz refletida apresenta (a) interferência construtiva total e (b) interferência destrutiva total?
Passo 1
A questão trata sobre interferência em filmes finos. A figura ilustra a situação com um filme fino de sabão cuja espessura é entre duas camadas de ar.
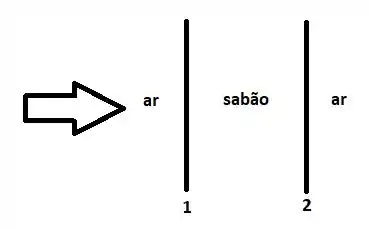
No caso temos que . Assim, na reflexão que ocorre na interface 1 há mudança de fase enquanto que na interface 2 não há. Assim, além da diferença de caminho, devemos somar na defasagem entre as ondas:
A diferença de caminho é (dobro da espessura da camada de sabão) e o fator que foi somada é devido ao fato de em uma das reflexões a fase ter invertido enquanto na outra não! É importante lembrar que:
Passo 2
No item (a) queremos que a interferência seja construtiva, de modo que a fase deve ser múltipla inteira de :
Portanto,
Como queremos saber quantos comprimentos de onda estarão na faixa entre e , tomando :
Para :
Assim, os valores possíveis de para que o comprimento de onda esteja na faixa visível são
Portanto, para quatro comprimentos de onda a interferência será construtiva!
Passo 3
Já para interferência destrutiva, devemos ter
Assim,
Para :
Já para :
Assím, nessa faixa, os valores de para que a interferência seja destrutiva são
Portanto, são três comprimentos de onda!
Resposta
Construtiva: 4
Destrutiva: 3
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 104-55.
A reflexão de um feixe de luz branca que incide perpendicularmente em uma película uniforme de sabão suspensa no ar apresenta um máximo de interferência em , e o mínimo mais próximo está em .
Se o índice de refração da película é , qual é a sua espessura?
Passo 1
O problema nos dá informações para usarmos tanto as condições de interferência construtiva quanto de interferência destrutiva.
Interferência Construtiva
Interferência Destrutiva
Porém não temos a ordem do máximo e do mínimo para podermos usar qualquer uma das duas separadas.
Temos 2 formas de fazer esse problema.
A primeira é a seguinte: manipulando as expressões acima, podemos encontrar a espessura do filme para diferentes ordens (valores de ) com nossos dois comprimentos de onda.
Então, nós listamos esses valores da espessura e vemos qual se repete nas nossas duas listas.
Passo 2
Para o segundo método, temos que perceber o seguinte:
O primeiro mínimo ocorre pra uma situação onde a espessura da película é quase zero (consideramos ). Assim, o primeiro máximo fica logo antes do segundo mínimo.
Mas por que esse comentário?
Porque o mínimo mais próximo do máximo de ordem corresponde ao mínimo de ordem .
Passo 3
Vamos considerar que . Então, manipulando as equações:
Substituindo em :
E com isso, temos uma expressão pra espessura .
Passo 4
O comprimento de onda que causa um máximo de interferência é . O comprimento de onda que causa um mínimo é .
O índice de refração da bolha de sabão é de .
Substituindo tudo isso na equação anterior:
Resposta
A espessura do filme é de aproximadamente .
Exercício Resolvido #4
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 100-pergunta 11.
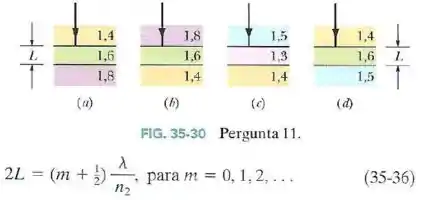
A Fig.35-30 mostra quatro situações nas quais a luz incide perpendicularmente em um filme fino de largura situado entre placas muito mais espessas feitas de materiais diferentes. Os índices de refração são dados.
Em que situações a Eq.35-36 corresponde à condição para que a intensidade da onda refletida seja máxima (ou seja, para que o filme pareça claro)?
Passo 1
Quando a luz reflete de um meio com menor índice de refração em um meio com maior índice de refração, ela sofre uma mudança de fase de meio comprimento de onda.
Para a reflexão em filmes finos, temos um raio que atravessa o filme, refletindo no fundo dele, e outro que reflete no topo.
A equação dada representa a condição de interferência construtiva no caso em que apenas um desses dois raios sofra mudança de fase por reflexão.
Passo 2
Outra forma de ver essa discussão é lembrar dos casos possíveis.
Os únicos dois casos onde essa equação não representa a condição de intensidade máxima é no caso em que e , ou seja, nenhuma mudança de fase ou duas mudanças de fase.
Esses dois são os casos das alternativas (a) e (b) apenas.
Com isso, vemos que os casos onde a equação dada é a condição de interferência construtiva são as alternativas (c) e (d).
Resposta
As alternativas (c) e (d) seguem a condição apresentada para máximo de intensidade.
Exercício Resolvido #5
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 103-35.
Os diamantes de imitação usados em bijuteria são feitos de vidro com índice de refração . Para que reflitam melhor a luz, costuma-se revesti-los com uma camada de monóxido de silício de índice de refração .
Determine a menor espessura da camada de monóxido de silício para que uma onda de comprimento de onda e incidência perpendicular sofra interferência construtiva ao ser refletida pelas duas superfícies da camada.
Passo 1
Neste problema, temos o nosso filme fino (camada de monóxido de silício com ) com ar de um lado () e vidro de outro ().
Com isso, a luz que vem do ar e reflete no topo do filme vai sofrer uma mudança de fase de meio comprimento de onda (), mas a luz que reflete no fundo do filme (na interface do monóxido de silício com o vidro) não vai ().
A condição de interferência construtiva se torna:
Onde é a espessura do filme.
Passo 2
Queremos a menor espessura para a qual a interferência vai ser construtiva. Logo, pegamos . Substituindo:
O enunciado nos diz que e que . Nossa espessura será:
Resposta
A menor espessura para que uma onda com sofra interferência construtiva ao refletir no filme é .
Exercício Resolvido #6
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 108-98.
A lente de uma câmara, com índice de refração maior que , é revestida com um filme fino transparente com um índice de refração de para eliminar por interferência a reflexão de luz com comprimento de onda que incide perpendicularmente na lente.
Que múltiplo de corresponde à espessura mínima de um filme que atende a essas especificações?
Passo 1
O filme na lente da câmara () está entre uma camada de ar () externa e o vidro da lente (). Podemos ver que para esses índices de refração temos:
Indicando que tanto a luz que é refletida no topo do filme quanto a refletida no fundo do filme sofrem uma mudança de fase de meio comprimento de onda, o que faz com que tenhamos uma situação semelhante a de não ter havido nenhuma mudança de fase.
As condições de interferência destrutiva (que elimina a reflexão) vão ser:
Como buscamos a espessura mínima possível usamos .
Passo 2
Assim, a espessura que procuramos, em múltiplos do comprimento de onda é:
Lembrando que
Resposta
A espessura mínima do filme que atende essas especificações é de comprimentos de onda.
Exercício Resolvido #7
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 100-10.
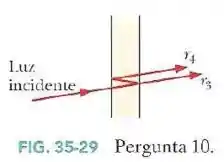
A Fig.35-29 mostra a passagem de um raio de luz perpendicular (mostrado com uma pequena inclinação para tornar a figura mais clara) por um filme fino suspenso no ar.
- O raio sofre uma mudança de fase por reflexão?
- Qual é a mudança de fase por reflexão fo raio , em comprimentos de onda?
- Se a espessura do filme é , qual é a diferença de percurso entre os raios e ?
Passo 1
a)
O raio é o que é refratado duas vezes (entrando e saindo do filme fino) e por isso ele não sofre nenhuma mudança de fase por reflexão.
Passo 2
b)
O raio é refletido duas vezes dentro do filme fino e depois é transmitido para o outro lado. Como ele reflete na interface filme/ar por dentro do filme, que tem um índice de refração maior que o ar, ele não sofre mudança de fase nessas reflexões.
Logo, a mudança de fase por reflexão do raio é de zero comprimentos de onda.
Passo 3
c)
O raio atravessa uma vez a espessura do filme. Logo:
Já o raio atravessa três vezes a espessura do filme (primeiro ele atravessa, é refletido, atravessa mais uma vez, é refletido novamente e atravessa uma terceira vez).
A diferença de percurso entre os dois raios será:
Resposta
a)
O raio não sofre mudança de fase por reflexão.
b)
O raio não sofre mudança de fase por reflexão.
c)
Exercício Resolvido #8
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 109-114
Um filme fino () é depositado em uma placa de vidro () e iluminado com uma luz cujo comprimento de onda no ar é . A luz incide perpendicularmente na placa.
Qual é a espessura mínima (diferente de zero) para que o filme:
- Transmita o máximo de luz.
- Reflita o máximo de luz.
Passo 1
Primeiro, temos que tomar cuidado para não cair em armadilhas do enunciado. O enunciado diz que o filme fino é depositado em uma placa de vidro. Isso significa que de um dos lados do filme teremos a placa de vidro.
Contudo, do outro lado nós teremos o mesmo que antes: ar.
Passo 2
a)
Dos raios de luz transmitidos, um não sofre nenhuma reflexão, e o outro sofre duas reflexões: uma na interface filme/vidro e uma na interface filme/ar, ambas por dentro do filme fino.
Como o índice de refração do filme é menor que o do vidro, na primeira reflexão o raio sofre mudança de fase de meio comprimento de onda. Na segunda reflexão, pelo índice de refração do filme ser maior que o do ar, o raio não sofre nada.
Além da diferença de percurso, teremos então mais meio comprimento de onda de diferença de fase.
A diferença de percurso é de , onde é a espessura do filme. As condições para transmitir o máximo de luz são:
Como queremos a espessura mínima, usamos o menor valor .
O comprimento de onda da luz é e o índice de refração do filme é .
Passo 3
b)
Para a reflexão da luz, teremos dois raios sofrendo uma reflexão cada. Um sofre uma reflexão no topo do filme fino e, como ele está se propagando de um meio com menor índice de refração para um meio com maior, ele sofre mudança de fase.
O outro reflete no fundo do filme fino, e sofre mudança de fase, pois ele se propaga no filme com .
A condição para refletir o máximo de luz vai ser:
Para a menor espessura, usamos o menor valor depois do zero, , e temos:
Resposta
a)
b)
Exercício Resolvido #9
––Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 103-36.
Um feixe de luz branca incide perpendicularmente, de cima para baixo, em um filme fino horizontal colocado entre placas espessas de dois materiais. Os índices de refração são para o material de cima, para o filme fino e para o material de baixo.
A espessura do filme é . Dos comprimentos de onda da luz visível ( a ) que resultam em interferência construtiva total para um observador situado acima do filme, qual é:
- O maior comprimento de onda?
- O menor comprimento de onda?
- Os materiais e o filme são aquecidos, o que faz a espessura do filme aumentar. A interferência construtiva total passa a ocorrer para um comprimento de onda maior ou menor?
Passo 1
A questão trata sobre interferência em filmes finos. A figura ilustra a situação com um filme fino com espessura colocado entre dois meios:
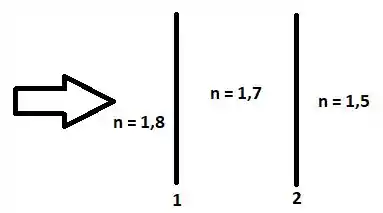
Nas reflexões nas duas interfaces não há mudança de fase, de modo que só devemos considerar a diferença de caminho:
Como
Passo 2
Queremos que a interferência seja construtiva:
Assim,
Para :
Já para :
Assim, os possíveis valores de na faixa considerada são
Passo 3
Isolando , temos que
O maior comprimento de onda com interferência construtiva ocorre para :
Já o menor ocorre para :
Se aquecermos o filme, ele aumenta de tamanho. Assim, como é proporcional a , o comprimento de onda vai aumentar!
Resposta
Maior
Exercício Resolvido #10
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 106-78.
Um filme fino de um certo líquido é mantido em um disco horizontal, com ar dos dois lados do filme. Um feixe de luz com um comprimento de onda de incide perpendicularmente ao filme, e a intensidade da reflexão é medida.
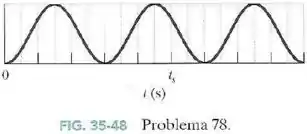
A Fig.35-48 mostra a intensidade em função do tempo ; a escala do eixo horizontal é definida por . A intensidade muda por causa da evaporação nas duas superfícies do filme.
Suponha que o filme é plano, que as duas superfícies do filme são paralelas e que o filme tem um raio de e um índice de refração de . Suponha também que o volume do filme diminui a uma taxa constante.
Determine essa taxa.
Passo 1
Primeiramente, vamos colocar a taxa da variação do volume em termos que saibamos calcular.
Como o volume é igual a área da base multiplicado pela altura, temos:
Onde a altura do filme é na verdade a espessura do mesmo. Como a taxa de variação do volume é constante, podemos substituir nossas derivadas:
Passo 2
Agora precisamos de uma variação de espessura cujo tempo de variação nós saibamos.
De fato, tem uma variação que sabemos calcular: a variação de espessura entre um mínimo de intensidade e outro, correspondendo a interferência destrutiva.
A condição de interferência destrutiva é dada por:
A altura é dada por:
Como o líquido está evaporando, a altura está diminuindo. Isso significa que estamos indo de um mínimo de ordem para um de ordem . A nova altura será:
Passo 3
Ok, temos a variação de espessura entre dois mínimos, mas quanto tempo leva essa variação?
O gráfico tem uma escala de pra cada unidade do eixo do tempo. Assim, o tempo entre dois mínimos é de .
Passo 4
A taxa de variação da altura vai ser:
Passo 5
Pra chegarmos na variação do volume, ainda precisamos da área do disco.
A área da base do disco é dada por , sendo que .
O nosso disco tem então uma área de
Passo 6
Agora sim, podemos encontrar a taxa de variação do volume. Juntando os dois cálculos anteriores:
Resposta
A taxa de variação do volume é de .
Exercício Resolvido #11
UFRJ, Física 4, Prova 1, 2011.2, Questão M5.
Um raio de luz monocromática incide perpendicularmente em um filme fino de água de espessura , sobre um bloco de vidro de espessura como mostrado na figura abaixo.
Dois observadores, e , determinam o critério para que a diferença de fase total dos raios emergentes leve a uma interferência destrutiva.
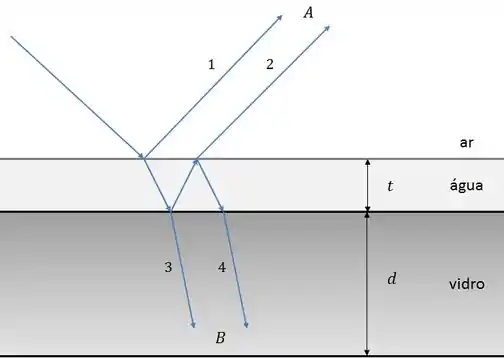
De acordo com os observadores e, respectivamente, a interferência será destrutiva quando:
- ;
- ;
- ;
- ;
- ;
- Nenhuma das anteriores
Passo 1
Vamos analisar o problema de dois pontos de vista diferentes, ok?
Observador :
Para o raio chegar ao observador ele é apenas refletido na superfície da água.
Já para o raio chegar ao observador , inicialmente ele é refratado quando passa pela superfície da água e refletido quando incide sobre a superfície do vidro, passando para o ar novamente ao incidir sobre a superfície da água.
Assim, a diferença de caminho é dada por:
E como essa diferença de caminho se refere quando o raio está na água:
Como os dois raios sofrem uma reflexão, cada, ambos estão em fase.
Do ponto de vista do observador , para que os dois raios sofram interferência destrutiva, é necessário que a diferença de caminhos entre eles seja dada por:
Logo:
Passo 2
Observador :
O raio não sofre nenhuma reflexão para chegar ao observador .
Para o raio chegar ao observador , é necessário que ele sofra duas reflexões, a primeira sobre a superfície do vidro e a segunda sobre a superfície da água.
Logo, os raios e estão fora de fase, de forma que, para que haja interferência destrutiva, a diferença de caminhos dos dois é dada por:
Assim, a diferença de caminho é dada por:
E como essa diferença de caminho se refere quando o raio está na água:
Logo:
Resposta
Letra (c):
Exercício Resolvido #12
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 108-104.
Uma placa de vidro com um índice de refração de deve ser revestida com um filme fino de um material com um índice de refração de para que uma luz verde com um comprimento de onda no ar de seja transmitida preferencialmente através de uma interferência construtiva.
- Qual é a espessura mínima do filme para que esse objetivo seja conseguido?
- Por que outras partes do espectro visível também não são transmitidas preferencialmente?
- A transmissão de alguma(s) cor(es) é reduzida significativamente? Qual ou quais?
Passo 1
a)
Temos de um lado do filme de índice de refração uma placa de vidro com e do outro lado o ar ().
Nesse caso, para a transmissão, temos um raio que não sofre nenhuma reflexão e um que sofrerá duas, ambas sem mudança de fase (pois é o maior dentre os três índices).
O máximo de transmissão será:
Sendo o comprimento de onda e a espessura a menor possível (por isso ):
Passo 2
b)
Com a espessura fixa, os comprimentos de onda que serão transmitidos preferencialmente são dados pelas ordens de máximo de transmissão, com
O que faz com que apenas comprimentos de onda específicos sejam transmitidos preferencialmente.
Quanto maio o , menor o comprimento de onda. O segundo a ter um máximo de transmissão () é:
Que já está fora do espectro visível. Os próximos serão ainda menores que o comprimento de onda do espectro visível.
Passo 3
c)
Para uma cor ser significativamente reduzida, ela precisa ter um mínimo de transmissão.
O comprimento de onda diminui com a ordem do mínimo, e o de primeira ordem então será o único a se encontrar no espectro visível.
Resposta
a)
b)
Porque elas não seguem as condições de máximo de transmissão.
c)
Sim, a da cor com comprimento de onda (azul-violeta).