Espectro Atômico
Teoria
Fala aí, seja muito bem vindo ao Responde Aí! Bora aprender sobre Espectros Atômicos?!
O que é um Espectro Atômico
Os átomos absorvem e emitem luz de vários comprimentos de onda. Porém, uma coisa que nunca havia sido bem compreendida era que essas emissões e absorções eram discretas. O que isso quer dizer?
Quer dizer que apenas valores bem específicos de comprimentos de onda eram emitidos e absorvidos. O conjunto de comprimentos de onda emitidos ou absorvidos por um átomo é chamado espectro atômico.
📢 Clique para ver mais:
Espectro Atômico do Hidrogênio
O átomo mais simples possível é o hidrogênio, o espectro de absorção do hidrogênio tem essa carinha aqui:
As linhas do espectro de hidrogênio não consistem apenas do espectro visível como a nossa imagem do ferro: ele tem linhas na região do infravermelho e linhas na região do ultravioleta. Na verdade, o hidrogênio só emite e absorve quatro comprimentos de onda na faixa da luz visível.
Após vários experimentos encontrou-se uma expressão geral para todas as linhas do espectro do hidrogênio, tanto as da luz visível quanto outras.
Onde $n_{baixo}
Onde:
A constante
Cada nível de energia corresponde a um valor de
O hidrogênio tem apenas um elétron, que pode estar em diversos níveis eletrônicos (camadas) que dão diferentes energias para o átomo.
Você também pode conferir esse conteúdo em vídeo:
Variação de Energia
Quando um átomo de hidrogênio emite ou absorve luz, sua energia varia, e como sabemos da quantização da energia, podemos dizer que, em uma transição, temos:
Onde
Onde
Séries de hidrogênio
Todo o espectro atômico do hidrogênio é deduzido pela fórmula que vimos acima. Contudo, ao longo da história, essa fórmula foi encontrada experimentalmente para diferentes faixas de comprimento de onda, e só depois de muito tempo que todas foram unificadas na fórmula dada acima e, depois de unificadas, explicadas por Bohr. Por isso o espectro de hidrogênio é dividido em diferentes classificações chamadas Séries do Hidrogênio. Cada uma dessas classificações corresponde a um valor de
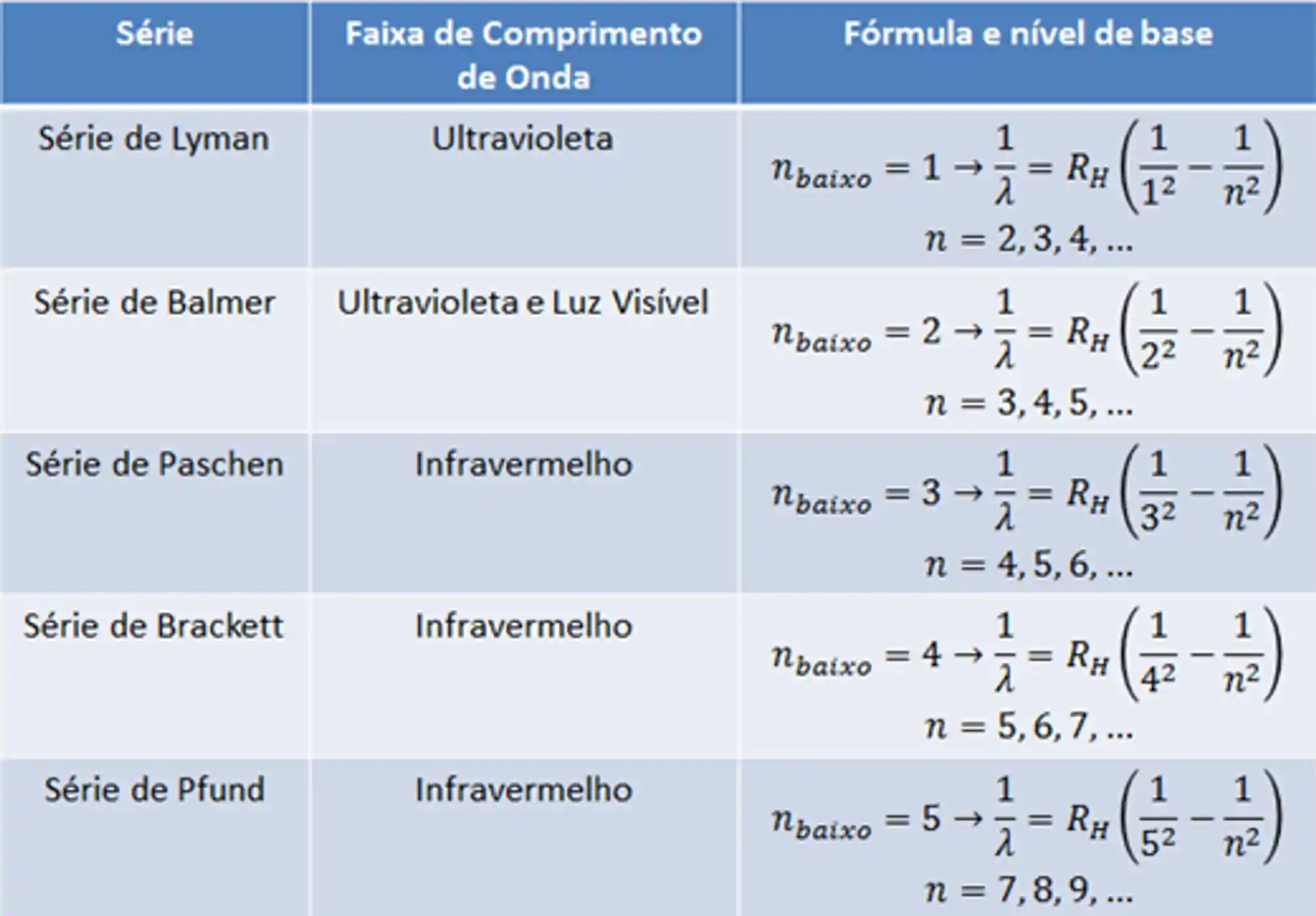
Na tabela acima podemos conferir as séries de Lyman, Balmer, entre outros.
Agora vamos praticar com exercícios?
Variação de Energia
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria.
Sabendo que a série de Lyman corresponde a transições por emissão que terminam em . Determine o comprimento de onda do fóton de maior comprimento de onda emitido e diga se ele está na faixa do visível.
Passo 1
Para determinar esse comprimento de onda máximo, precisamos lembrar da fórmula:
Fique tranquilo, essa fórmula deve estar na capa de sua prova!
Passo 2
Para a transição que estamos considerando, temos os seguintes dados:
Isso porque a série de Lyman tem como nível de base e a transição deve provir do nível logo acima para que o comprimento de onda seja o maior possível.
Agora é só substituir na fórmula, se liga no próximo passo!
Passo 3
Agora invertendo
Preste atenção nas unidades! Como a constante é dada em , teremos:
Passando para a medida usual, em , temos:
Sabendo que a faixa do visível está entre e , podemos perceber que o comprimento de onda emitido não está na faixa do visível.
Resposta
Não está na faixa do visível.
Exercício Resolvido #2
PUC-RIO, Física 4, Prova 3, 2012.2.
A série de Balmer para o Hidrogênio corresponde a transições eletrônicas que terminam no estado número quântico .
Determine o comprimento de onda do fóton de maior comprimento de onda emitido.
Obtenha a energia desse fóton.
Passo 1
Para determinar o comprimento de onda, devemos lembrar da relação para as transições do Hidrogênio:
Substituindo os valores dados e o valor da constante de Rydberg :
Passo 2
Para determinar a energia do fóton, precisamos lembrar da equação para a energia do fóton:
Lembrando que a constante , a energia, fica:
Resposta
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 242-37.
Qual é a razão entre o menor comprimento de onda da série de Balmer e o menor comprimento de onda da série de Lyman?
Passo 1
O comprimento de onda de qualquer série espectroscópica do hidrogênio é dado por:
Onde é a constante de Rydberg.
Para uma dada série é constante e temos que diminui com o aumento de , pois:
- Quando aumenta, aumenta.
- Quando aumenta, aumenta.
- Quando aumenta, diminui.
Passo 2
O menor comprimento de onda vai ser dado no limite em que .
Para a série de Balmer:
Passo 3
Para a série de Lyman:
E teremos então:
Resposta
Exercício Resolvido #4
PUC-RIO, Física 4, Prova 3, 2013.1
A série de Paschen para o Hidrogênio corresponde a transições eletrônicas que terminam no estado de número quântico .
Determine o comprimento de onda do fóton de maior comprimento de onda emitido.
Obtenha a energia desse estado inicial .
Passo 1
Para determinar o comprimento de onda, devemos lembrar da relação para as transições do Hidrogênio:
Substituindo os valores dados e o valor da constante de Rydberg :
Passo 2
Para as energias dos estados, temos:
Para o estado inicial , temos:
Resposta
Exercício Resolvido #5
PUC-RIO, Física 4, Prova 3, 2013.2.
A série de Brackett para o Hidrogênio corresponde a transições eletrônicas que terminam no estado de número quântico .
Determine o comprimento de onda do fóton de maior comprimento de onda emitido e diga se está na faixa do visível.
Obtenha a energia desse estado inicial em .
Passo 1
Sabemos que as transições de energia do hidrogênio podem ser relacionadas ao comprimento de onda pela seguinte fórmula:
Onde indica o estado incicial e final. E é a chamada constante de Rydberg.
Para os parâmetros que temos, a fórmula fica:
Substituindo o valor da constante, temos:
Não está na faixa do visível, pois .
Passo 2
Para determinar a energia do estado inicial devemos utilizar a seguinte fórmula para os estados:
Resposta
; Não está na faixa do visível pois .