Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

O Fóton

Ver Todos os Exercícios

Teoria

Fala aí, seja bem vindo ao Responde Aí! Bora bater um papo sobre a Energia de um fóton?!

O que é um Fóton?

Um fóton, também chamado de fotão, são minúsculos pacotes de energia que compõe a luz e são responsáveis por transportar a energia das radiações eletromagnéticas.

-Hãam? 😖

Pra ficar mais claro, eu vou te contar uma historinha e você vai entender qual é a do fóton!

Lá pra meados de 1900, a física começou a apresentar milhares de problemas. Uma série de fenômenos contrariavam completamente resultados da física clássica, e não adiantava dizer que os pontos experimentais do gráfico estavam errados porque não estavam!

Fótons
Fótons

Para resolver um desses pepinos, um físico chamado Max Planck fez uma hipótese que dizia que a luz não era bem uma onda que levava energia continuamente pra onde ela iluminava, na verdade ela cedia energia em pacotinhos, ou seja, era quantizada.

📢 Clique para ver mais:

Fórmula da Energia de um Fóton

Pra a gente calcular a energia de um fóton a gente usa a seguinte fórmula:

ó

Onde é a energia do fóton, é a frequência da luz e é a constante de Planck, igual a . A energia também pode ser descrita em função do comprimento de onda da luz usando a velocidade da luz. Dessa forma ficamos com:

ó

Onde é a velocidade da luz no vácuo, igual a .

Você também pode conferir esse conteúdo no vídeo abaixo! 👇

Propriedades Luminosas e Fóton

A gente pode relacionar algumas propriedades da luz com a ideia de energia quantizada.
Uma delas é a potência luminosa (P). A potência da luz é a energia que ela transfere para algum lugar em um dado tempo.

A potência luminosa se relaciona com a taxa de fótons emitidos pela fonte luminosa, que significa o número de fótons emitidos por unidade de tempo.

Sendo a potência e energia total da luz emitida em um dado tempo, se dividirmos essa energia pela energia de 1 fóton, podemos encontrar o número de fótons emitidos.

ó

A taxa de fótons emitidos será a potência luminosa dividida pela energia de um fóton. Quando a luz se propaga, toda a potência da fonte vai se espalhando na área que a luz se propaga. A intensidade é então essa potência dividida pela área que a luz se espalhou.

Dividindo a intensidade pela energia de 1 fóton, temos o fluxo de fótons:

óó

Onde N é a quantidade de fótons emitidos por unidade de tempo, A a área e o fluxo de fótons.

Momento Linear de um Fóton

As ondas eletromagnéticas possuem um momento linear que as permite empurrar objetos como satélites e caudas de cometa. Neste caso, os fótons também terão associados a si um momento linear e também poderão empurrar os outros. A magnitude do momento linear do fóton é dada por:

Porém, como tínhamos visto para os fótons:


Logo temos:


A direção e o sentido do momento linear do fóton são a direção e sentido de propagação da luz. Seja o vetor de propagação:

ó

Agora vamos praticar com exercícios?!

Fórmula da Energia de um Fóton

Propriedades Luminosas e Fóton

Momento Linear de um Fóton

Exercícios Resolvidos

Exercício Resolvido #1

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 208-4

A luz amarela de uma lâmpada de vapor de sódio usada em iluminação pública é mais intensa em um comprimento de onda de 589   n m .

Qual é a energia dos fótons com esse comprimento de onda?

Passo 1

A energia de um fóton é dada por:

E = h f

Porém podemos relacionar a frequência e o comprimento de onda da luz:

f λ = c

f = c λ

E assim:

E = h c λ

Sabemos que:

  • h ≅ 6,626 ∙ 10 - 34   J ∙ s
  • c ≅ 2,998 ∙ 10 8   m / s
  • λ = 589   n m = 589 ∙ 10 - 9   m (pelo enunciado)

E = 6,626 ∙ 10 - 34 ∙ 2,998 ∙ 10 8 589 ∙ 10 - 9 ≅ 3,3726   ∙ 10 - 19   J

Ou, em e V :

1   e V ≅ 1,602 ∙ 10 - 19 J  

E = 3,37 26   ∙ 10 - 19 1,602 ∙ 10 - 19 ≅ 2,11   e V

Resposta

E ≅ 3,3726   ∙ 10 - 19   J ≅ 2,11   e V

Exercício Resolvido #2

UFRJ, Física 4, Prova 2, 2011.2

Para quebrar a ligação química nas moléculas da pele humana e causar queimaduras solares, é necessário um fóton com energia de cerca de 3,50   e V .

O comprimento de onda da radiação que provoca queimaduras na pele é de cerca de:

  1. 724   n m
  2. 524   n m
  3. 244   n m
  4. 354   n m
  5. Nenhuma das anteriores.

Passo 1

Podemos associar a energia do fóton com o seu comprimento de onda a partir da equação:

E = h c λ

λ = h c E

Onde:

h = 4,136 × 10 - 15   e V   s ;

E = 3,50   e V ;

c = 3 × 10 8   m / s ;

Logo:

λ = 4,136 × 10 - 15 × 3 × 10 8 3,5

λ = 3,54 × 10 - 7   m = 354   n m

Resposta

Letra (d): 354   n m

Exercício Resolvido #3

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 209-27.

Um feixe de raios X tem um comprimento de onda de 35,0   p m .

  1. Qual é a frequência correspondente?

    2. Determine:

  2. A energia dos fótons do feixe.
  3. O momento dos fótons do feixe, em k e V / c .

Passo 1

Letra a)

A frequência e o comprimento de onda se relacionam por:

λ f = c

f = c λ

Onde:

  • c = 2,998 ∙ 10 8   m / s
  • λ = 35,0   p m = 35,0 ∙ 10 - 12   m

f = 2,998 ∙ 10 8 35 ∙ 10 - 12 ≅ 8,566 ∙ 10 18   H z

Passo 2

Letra b)

A energia dos fótons é dada por:

E = h f

Onde h = 6,626 ∙ 10 - 34   J ∙ s é a constante de Planck. Usando o resultado do item anterior:

E ≅ 6,626 ∙ 10 - 34 ∙ 8,566 ∙ 10 18 ≅ 56,758 ∙ 10 - 16   J = 5,6758 ∙ 10 - 15   J

Vamos ver quanto fica em e V . Temos que:

1   e V ≅ 1,602 ∙ 10 - 19 J

E ≅ 5,6758 ∙ 10 - 15   J ≅ 35   429,46   e V

Passo 3

Letra c)

O momento linear do fóton é dado por:

p l i n = E c

Encontramos no item anterior que E ≅ 35   429,46   e V ≅ 35,429   k e V .

p l i n = 35,429   k e V / c

Resposta

Letra a)

f ≅ 8,566 ∙ 10 18   H z

Letra b)

E ≅ 5,6758 ∙ 10 - 15   J ≅ 35   429,46   e V

Letra c)

p l i n = 35,429   k e V / c

Exercício Resolvido #4

Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 211-38.9

Uma fonte de luz de 75   W consome 75   W de potência elétrica.

Suponha que toda essa energia se transfira para a luz emitida com comprimento de onda 600   n m .

  1. Calcule a frequência da luz emitida.
  2. Quantos fótons por segundo a fonte emite?
  3. As respostas às partes (a) e (b) são iguais? A frequência da luz é a mesma que o número de fótons emitidos por segundo? Explique.

Passo 1

a) Calcule a frequência da luz emitida.

Podemos associar a frequência f e o comprimento de onda λ através da seguinte relação:

c = λ f → λ = c f

Onde:

c = 3 × 10 8   m / s ;

λ = 600   n m = 6 × 10 - 7 m ;

Logo:

f = 3 × 10 8 6 × 10 - 7 = 5,0 × 10 14   H z

Passo 2

b) Quantos fótons por segundo a fonte emite?

O problema nos dá a potência P que, por definição, é a taxa de variação da energia E por unidade de tempo.

Assim, 75   W = 75   J / s . Ou seja, a cada segundo são produzidos 75   J de energia.

Para descobrirmos quantos fótons a fonte emite por segundo, vamos calcular a energia de cada fóton e ver a quantidade correspondente a 75   J .

Passo 3

A energia do fóton é dada por:

E f ó t o n = h f

Onde:

h = 6,626 × 10 - 34   J   s ;

f = 5,0 × 10 14   H z ;

Logo:

E f ó t o n = 6,626 × 10 - 34 × 5,0 × 10 14

E f ó t o n = 3,313 × 10 - 19   J

Passo 4

O número de fótons emitidos por segundo é dado por:

n = E E f ó t o n = 75 3,313 × 10 - 19

n = 2,3 × 10 20   f ó t o n s

Passo 5

c) As respostas às partes (a) e (b) são iguais? A frequência da luz é a mesma que o número de fótons emitidos por segundo? Explique.

Não, ambos possuem significados físicos diferentes. A frequência está diretamente associada à energia do fóton e independe da potência da fonte.

Porém, o número de fótons emitidos por segundo depende da potência da fonte.

Resposta

a)

5,0 × 10 14   H z

b)

2,3 × 10 20 f ó t o n s / s

c)

Não.

Exercício Resolvido #5

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 208-7

Uma lâmpada ultravioleta emite luz com um comprimento de onda de 400   n m , com uma potência de 400   W .

Uma lâmpada infravermelha emite luz com um comprimento de onda de 700   n m , também com uma potência de 400   W .

  1. Qual das duas lâmpadas emite mais fótons por segundo?
  2. Quantos fótons por segundo essa lâmpada emite?

Passo 1

Letra a)

Vamos ver como calcular quantos fótons por segundo cada lâmpada emitiria.

Primeiro, vemos a energia de cada fóton:

E = h f = h c λ

Ou seja, quanto maior o comprimento de onda, menor a energia dos fótons.

Depois, vemos a energia que cada lâmpada emite por segundo. Uma potência de 1   W corresponde a 1   J / s , que é energia por segundo.

Assim, seja P a potência da lâmpada em Watts e E a energia dos fótons em Joules. O número de fótons por segundo será:

N = P E

Quanto menor a energia, maior o número de fótons emitidos.

Juntando as duas considerações, temos que quanto maior o comprimento de onda da luz, maior a quantidade de fótons emitidos.

A fonte com maior comprimento de onda é a lâmpada infravermelha, que emitirá mais fótons por segundo.

Passo 2

Letra b)

Como discutimos no item anterior, o número de fótons emitidos será dado por:

N = P E

Mas também vimos que:

E = h c λ

Logo:

N = P ∙ λ h c

Onde todos os termos devem estar com unidades do SI.

  • P = 400   W
  • λ = 700   n m = 700 ∙ 10 - 9   m
  • h ≅ 6,626 ∙ 10 - 34   J ∙ s
  • c ≅ 2,998 ∙ 10 8   m / s

Substituindo:

N = 400 ∙ 700 ∙ 10 - 9 6,626 ∙ 10 - 34 ∙ 2,998 ∙ 10 8 ≅ 14   095 ,   32 ∙ 10 17   f ó t o n s ≅ 1,41 ∙ 10 21   f ó t o n s

Resposta

Letra a)

A lâmpada infravermelha emite mais fótons por segundo.

Letra b)

N ≅ 1,41 ∙ 10 21   f ó t o n s

Exercício Resolvido #6

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 207-5.

O fóton A tem uma energia duas vezes maior que o fóton B .

  1. O momento do fóton A é menor, igual ou maior que o momento do fóton B ?
  2. O comprimento de onda do fóton A é maior, menor ou igual ao comprimento de onda do fóton B?

Passo 1

Letra a)

O momento linear de um fóton é dado por:

p l i n = E c

Onde E é a energia do fóton e c é a velocidade da luz.

Isso nos mostra que quanto maior a energia do fóton, maior seu momento linear.

Como a energia do fóton A é maior que a do fóton B , o momento do fóton A é maior que o do fóton B .

Passo 2

Letra b)

A energia de um fóton é dada por:

E = h f = h c λ

Rearrumando:

λ = h c E

Quanto maior a energia do fóton, menor seu comprimento de onda.

Como a energia de A é maior que a de B , o comprimento de onda de A é menor que o de B .

Resposta

Letra a)

O momento do fóton A é maior que o do fóton B .

Letra b)

O comprimento de onda do fóton A é menor que o do fóton B .

Exercício Resolvido #7

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 208-10.

Em condições ideais, o sistema de visão humano é capaz de perceber uma luz com um comprimento de onda de 550   n m se os fótons dessa luz forem absorvidos pela retina à razão de pelo menos 100 fótons por segundo.

Qual é a potência luminosa absorvida pela retina nessas condições?

Passo 1

Digamos que a potência luminosa absorvida pela retina é de P   W a t t s . Como 1   W = 1   J / s , isso significa que a retina absorve uma energia de P   J o u l e s a cada segundo.

Se cada fóton tiver uma energia de E   J o u l e s , então o número de fótons absorvidos em um segundo vai ser:

N = P E → P = N ∙ E

Pelo enunciado, sabemos que N = 100   f ó t o n s , o que nos dá:

P = 100 ∙ E

Passo 2

Agora, precisamos encontrar a energia de cada fóton.

A energia de 1 fóton vai ser:

E = h f = h c λ

O valor do comprimento de onda é dado pelo enunciado, e h e c são constantes:

  • h ≅ 6,626 ∙ 10 - 34   J ∙ s
  • c ≅ 2,998 ∙ 10 8   m / s
  • λ = 550   n m = 550 ∙ 10 - 9   m

Onde passamos todos os valores para Joules, metros e segundos.

E = h c λ ≅ 6,626 ∙ 10 - 34 ∙ 2,998 ∙ 10 8 550 ∙ 10 - 9 ≅ 3,61177 ∙ 10 - 19   J

P = 100 ∙ E ≅ 3,6 ∙ 10 - 17   W

Resposta

P ≅ 3,6 ∙ 10 - 17   W

Exercício Resolvido #8

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 208-11

Uma lâmpada de sódio de 100   W ( λ = 589   n m ) irradia energia uniformemente em todas as direções.

  1. Quantos fótons por segundo são emitidos pela lâmpada?
  2. A que distância da lâmpada uma tela totalmente absorvente absorve fótons à taxa de 1,00   f ó t o n / c m 2 ∙ s ?
  3. Qual é o fluxo de fótons (fótons por unidade de área e por unidade de tempo) em uma pequena tela situada a 2,00   m da lâmpada?

Passo 1

Letra a)

A potência da lâmpada é de P = 100   W .

A energia individual de cada fóton é:

E = h c λ

Onde:

  • h = 6,626 ∙ 10 - 34   J ∙ s
  • c = 2,998 ∙ 10 8   m / s
  • λ = 589   n m = 589 ∙ 10 - 9   m

E = 6,626 ∙ 10 - 34 ∙ 2,998 ∙ 10 8 589 ∙ 10 - 9 ≅ 3,3726 ∙ 10 - 19   J

A taxa de emissão de fótons vai ser:

N = P E ≅ 100 3,3726 ∙ 10 - 19 ≅ 2,965 ∙ 10 20   f ó t o n s / s e g u n d o

Passo 2

Letra b)

Como a lâmpada irradia luz uniformemente em todas as direções, isso significa que a luz se espalha numa esfera com centro na fonte de luz.

A superfície de uma esfera é dada por:

A = 4 π r 2

Assim, o número de fótons emitidos por unidade de tempo por unidade de área vai ser:

N - = N A = N 4 π r 2

Passo 3

Nós queremos achar a distância r correspondente a um fluxo de fótons de N - = 1,00   f ó t o n / c m 2 ∙ s .

Rearranjando a fórmula e substituindo os valores:

r 2 = N 4 π N - → r = N 4 π N -

r ≅ 2,965 ∙ 10 20 4 π ∙ 1,00 ≅ 0,4857 ∙ 10 10   c m = 4,857 ∙ 10 7 m

Passo 4

Letra c)

Para uma distância de r = 2,0   m da fonte luminosa, o fluxo de elétrons vai ser:

N - = N 4 π r 2 ≅ 2,965 ∙ 10 20 4 π ∙ 2 2 ≅ 5,899 ∙ 10 18   f ó t o n s / m 2 ∙ s

Resposta

Letra a)

N ≅ 2,965 ∙ 10 20   f ó t o n s / s e g u n d o

Letra b)

r ≅ 4,857 ∙ 10 7 m

Letra c)

N - ≅ 5,899 ∙ 10 18   f ó t o n s / m 2 ∙ s

Exercício Resolvido #9

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 209-12

Um detector de luz possui uma área útil de 2,00 × 10 - 6   m 2 e absorve 50 % da luz incidente, cujo comprimento de onda é 600   n m . O detector é colocado diante de uma fonte luminosa isotrópica, a 12,0   m da fonte.

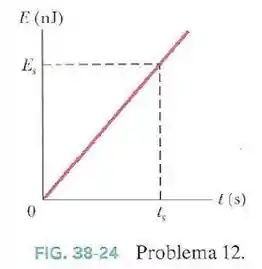
A Fig.38-24 mostra a energia E emitida pela fonte em função do tempo t . A escala do eixo vertical é definida por E s = 7,2   n J e a escala do eixo horizontal é definida por t s = 2,0   s .

Quantos fótons por segundo são absorvidos pelo detector?

Passo 1

Vamos fazer um passo a passo partindo da fonte luminosa até chegar ao olho.

A potência da fonte é a energia que ela emite por unidade de tempo, ou seja:

P l u z = E t

Pela escala do gráfico, E s = 7,2   n J = 7,2 ∙ 10 - 9   J corresponde a t s = 2,0   s .

P l u z = 7,2 ∙ 10 - 9 2 = 3,6 ∙ 10 - 9   W

Passo 2

Como a fonte é uma fonte isotrópica, a luz se espalha uniformemente em todas as direções, descrevendo uma esfera com centro na fonte.

Assim, a potência luminosa se espalha ao longo de uma esfera, e a intensidade será:

I = P l u z A l u z = P l u z 4 π r 2

Onde r = 12,0   m é a distância que a luz percorre.

I = 3,6 ∙ 10 - 9   4 π ∙ 12 2 ≅ 1,989 ∙ 10 - 12   J / m 2 ∙ s

Passo 3

A mesma intensidade atinge o detector.

I = P d A d → P d = I ∙ A d

A área do detector é A d = 2,00 ∙ 10 - 6   m 2 .

P d ≅ 1,989 ∙ 10 - 12 ∙ 2 ∙ 10 - 6 ≅ 3,979 ∙ 10 - 18   W

Porém, de toda essa potência que atinge o detector, apenas 50 % é absorvida. A potência P absorvida é:

P = 0,5 ∙ P d ≅ 1,989 ∙ 10 - 18   W

Passo 4

A taxa de fótons absorvidas vai ser a taxa de energia absorvida (a potência) dividida pela energia individual dos fótons.

A energia de cada fóton é:

E = h c λ

Onde:

  • h = 6,626 ∙ 10 - 34   J ∙ s
  • c = 2,998 ∙ 10 8   m / s
  • λ = 600   n m = 600 ∙ 10 - 9   m = 6 ∙ 10 - 7   m

E = 6,626 ∙ 10 - 34 ∙ 2,998 ∙ 10 8 6 ∙ 10 - 7 ≅ 3,3108 ∙ 10 - 19   J

Taxa de Fótons:

N = P E ≅ 1,989 ∙ 10 - 18   3,3108 ∙ 10 - 19 ≅ 6,008   f ó t o n s / s e g u n d o

Resposta

N ≅ 6,008   f ó t o n s / s e g u n d o

Exercícios de Livros Relacionados

Em 1987, um laser no Laboratório Nacional de Los Alamos produziu um flash que durou 1 × 10–12 se uma potência de 5 × 1015 W. Estime o número de fótons emitidos, assumindo que todos eles tenham comprim
Uma fonte de 100 W irradia luz de comprimento de onda 600 nm uniformemente em todas as direções. Um olho que foi adaptado ao escuro tem uma pupila de 7 mm de diâmetro e pode detectar a luz se pelo men
Um laser de safira de titânio e bloqueado por modo tem um comprimento de onda de 850 nm e produz 100 milhões de pulsos de luz por segundo. Cada pulso tem uma duração de 125 femtossegundos (1 fs = 10–1
O comprimento de onda da luz vermelha emitida por um laser de hélio-neon de 3,00 mW é de 633 nm. Se o diâmetro do raio laser é de 1,00 mm, qual é a densidade dos fótons no raio? Suponha que a intensid
Os lasers usados em uma rede de telecomunicações normalmente produzem luz com comprimento de onda próximo a 1,55 μm. Quantos fótons por segundo estão sendo transmitidos se esse laser possui uma potênc