Velocidade e Momento Linear do Centro de Massa
Teoria
Velocidade do Centro de Massa
Imagine o sistema de partículas desenhado na figura abaixo, considere que , e tem o mesmo valor . Podemos representar todas as partículas do sistema pelo centro de massa:
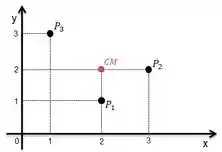
Digamos que as partículas e tenham as respectivas velocidades: , e , todas na direção como calcular a velocidade do centro de massa?
Que tal usar uma média ponderada das velocidades dos objetos do sistema, onde o peso da média é a massa de cada objeto.
E através da direção e do sentido da Velocidade do Centro de Massa podemos descrever o movimento do Centro de Massa.
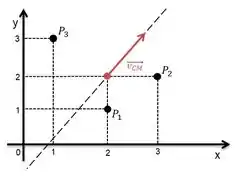
Onde representa a Velocidade do Centro de Massa de cada objeto do sistema. Assim as partículas mais pesadas tem maior possibilidade de alterar a direção e o sentido do movimento do Centro de Massa. No nosso exemplo todas as partículas tem massa , então:
E substituindo temos:
Imaginemos agora o mesmo problema porém a velocidade da partícula aponta para a direção , como resolver essa parada?
Nesse caso temos que separar as componentes dos vetores nos eixos x, y, e z. Generalizando poderíamos escrever:
E pro nosso exercício vai ficar:
E a gente faz o cálculo:
Como temos
E para temos apenas a velocidade da primeira partícula atuando já que as outras são zero.
Daí:
Mas sabemos que o momento linear de uma partícula vale:
E de um sistema de partículas:
Podemos então reescrever a equação da velocidade do centro de massa da seguinte forma
Momento Linear do Centro de Massa
Podemos brincar com a última fórmula e reescrevê-la isolando o Momento Linear, dessa forma podemos calcular o Momento Linear a partir do valor das massas das partículas e da Velocidade do Centro de Masssa do objeto:
Em um colisão em que existir a Conservação do Momento Linear, podemos afirmar que a velocidade do centro de massa do sistema irá se manter a mesma:
Bora fazer um exemplo disso aqui pra entender legal, imagina o seguinte sistema:
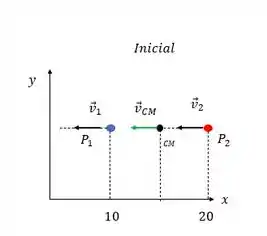
As partículas possuem a mesma massa e a azul tem velocidade enquanto que a outra partícula tem velocidade de , se após a colisão a velocidade da partícula azul passou a ser mostre que a velocidade inicial e final do centro de massa é a mesma.
Bom vamos usar primeiro a conservação de momento linear pra encontrar a velocidade final da partícula e por esse motivo aqui poderemos dizer que a velocidade final do centro de massa tabém será a mesma.
Como ambas possuem a mesma massa o problema fica dependendo das velocidades:
Substituindo os valores:
A velocidade do centro de massa inicialmente era:
E substituindo os valores:
E a velocidade final do centro de massa é:
E substituindo os valores:
E após as partículas colidirem as velocidades finais e a do centro de massa tem o mesmo sentido da figura e o centro de massa mantém a mesma posição entre as partículas.
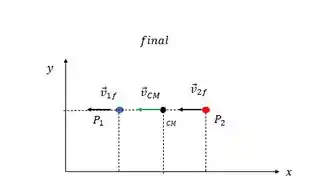
Show, vamos dar uma olhadas em uns exercícios!
Momento Linear do Centro de Massa
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ – 2ª Prova – 2013.1
Duas partículas e de massas e movem-se em movimento retilíneo uniforme com velocidades e respectivamente. Num dado instante ocorre uma colisão entre elas totalmente inelástica, pode-se afirmar, sobre a velocidade do centro de massa das partículas que:
Depois da colisão ;
Antes da colisão ;
Depois da colisão ;
Antes da colisão e depois da colisão ;
Depois da colisão ;
Passo 1
Vimos que a velocidade do centro de massa pode ser escrita como
Desta forma como ocorre uma colisão temos que há conservação de momento linear
Assim temos que em uma colisão a velocidade do centro de massa irá se conservar e por isso
Sabendo disso já elimiamos a alternativa
Passo 2
Agora basta calcula a velocidade do centro de massa inicial para acharmos a resposta.
As velocidades estão na forma vetorial, então vamos usar a fórmula da velocidade do centro de massa na forma vetorial.
Então
Como a velocidade não muda temos que
Resposta
Letra
Exercício Resolvido #2
PUC-RIO – 2ª Prova – 2013.2
A figura mostra dois veículos que colidem de modo totalmente inelástico num cruzamento . A velocidade dos escombros conjuntos tem valor imediatamente após a colisão e direção que faz com o eixo . O veículo , que vinha no eixo da figura, tem massa , e o veículo tem massa . Considere o sistema isolado durante a colisão.
Forneça o vetor momento linear do centro de massa do sistema imediatamente depois da colisão, , e imediatamente antes da colisão, . Justifique.
Qual a velocidade escalar de cada veículo antes da colisão?
Forneça o vetor força que atuou sobre o veículo , , sabendo que a colisão teve duraçãoo de .
Passo 1
Quando estamos lidando com uma colisão totalmente inelástica, devemos lembrar que nesse tipo de colisão, os objetos envolvidos tem a mesma velocidade final, ou seja, eles saem juntos.
Para calcular o vetor momento dos corpos depois da colisão, devemos primeiro lembrar da sua definição:
Depois da colisão, pelo fato de os carros terem a mesma velocidade, temos:
Para determinar o vetor momento em relação aos eixos, vamos decompor ele em suas componentes e .
Em , temos:
Substituindo os valores, temos:
Em , temos:
Substituindo os valores, temos:
Portanto, o vetor momento depois da colisão é:
Por se tratar de um sistema isolado, onde forças externas não estão atuando, podemos aplicar a conservação do momento linear, desse modo o vetor momento do sistema antes da colisão será igual ao vetor momento linear depois da colisão:
Passo 2
Pelo fato de os carros estarem posicionados conforme mostra a figura, percebemos, que antes da colisão, a componente do vetor momento linear é devida exclusivamente ao veículo , que vinha no eixo .
Analogamente a componente do vetor momento linear é devida exclusivamente ao veículo , que vinha no eixo . Com isso em mente, temos:
Para o veículo :
Substituindo os valores, temos:
Para o veículo :
Substituindo os valores, temos:
Passo 3
Para determinar a força que atuou sobre o veículo , precisamos lembrar do teorema Força-Impulso, ele nos diz:
Como temos a velocidade do veículo antes e depois da colisão , podemos achar a força
Substituindo os valores, temos:
Veja que estamos decompondo a velocidade final, pois queremos descobrir o vetor força, e a melhor maneira é determinar as componentes em separado.
Resposta
;
Exercício Resolvido #3
PUC-RIO – 2ª Prova – 2008.2
Um disco de borracha de se movimenta inicialmente com vetor velocidade sobre uma superfície horizontal sem atrito e sofre uma colisão com um disco de borracha de movendo-se inicialmente com vetor velocidade . Considere as seguintes situações:
Se o vetor velocidade e o vetor velocidade do centro de massa , calcule o vetor velocidade .
Passo 1
O problema envolve um colisão e nos dá a velocidade inicial de uma partícula e a velocidade do centro de massa, isso nos faz pensar em relacionar a velocidade do centro de massa com o momento linear do sistema.
Seria tão bom se tivéssemos uma fórmula para isso. OPA! Nós temos hahaha
Show, vamos continuar! :D
Passo 2
Vamos abrir o momento
sendo e a massa dos discos de borracha, um de e outro de .
E como , vamos ter
Passo 3
Passando isso pra frações que é melhor, dá:
Passo 4
Separando da forma , isso dá:
Passo 5
E pelo enunciado,
Ou seja:
Portanto, vamos ter
A primeira equação fica:
E pela segunda equação:
Portanto,
Resposta
Exercício Resolvido #4
UFRJ – 2ª Prova – 2012.2
Um bloco deslocando-se com momento linear , colide com um bloco de momento linear , onde é constante. Suponha que não há força externa. Após a colisão o centro de massa do sistema segue, de acordo com o sistema de coordenadas ortogonais e os respectivos vetories unitários , e :
na direção e sentido negativo;
na direção e sentido negativo;
na direção e sentido positivo;
na direção e sentido positivo;
em uma direção formando um ângulo com os eixos e .
Passo 1
Como não temos forças externas o momento linear irá se conservar durante a colisão. Assim pela equação da velocidade do centro de massa
Vemos que a velocidade do centro de massa não se altera e assim o centro de massa mantem seu movimento, como vimos na teoria. Então basta encontrarmos a velocidade para saber como ele está se movendo.
Passo 2
Já vimos que a velocidade do centro de massa pode ser calculado vetorialmente com
Sabemos que o momento linear de cada partícula é
Então o momento linear do sistema é
Passo 3
Substituindo na fórmula da velocidade do centro de massa
Repara que a velocidade do centro de massa só vai ter componente , que é componente horizontal. Então ele segue na direção no sentido positivo
Resposta
Letra
Exercício Resolvido #5
PUC-RIO – 2ª Prova – 2013.1
Um disco de massa , inicialmente em repouso sobre uma superfície horizontal sem atrito, sofre uma colisão não-frontal com um segundo disco de massa , movendo-se inicialmente ao longo do eixo com velocidade escalar constante . Após a colisão, o segundo disco passa a ter velocidade escalar e sai a um ângulo em relação ao eixo positivo, veja a figura. Use o sistema de coordenadas fornecido.
Ache o vetor velocidade do centro de massa dos discos antes da colisão.
Em termos dos vetores unitários e , determine o vetor velocidade do disco 1 após a colisão. Calcule o ângulo com que ele emerge.
Determine o vetor velocidade do centro de massa do sistema após a colisão, explicitamente usando seu resultado da letra . Compare com o resultado da letra e discuta.
Passo 1
Basta utilizar a fórmula para encontrar a velocidade do centro de massa:
Passo 2
Como o sistema é isolado (não há forças externas atuando e as forças internas são produzidas em par ação-reação, se anulando), a resultante das forças que age sobre o sistema é nulo e desta forma o momento linear total do sistema é conservado.
Para encontrar a direção, basta imaginar um triângulo em que o eixo é o cateto oposto e o eixo é o cateto adjacente. Temos então um ângulo com o eixo , onde:
Logo:
Passo 3
Podemos utilizar novamente a fórmula:
Entretanto, como falamos antes, o momento linear é conservado, ou seja:
Logo, a velocidade do centro de massa é sempre a mesma. Logo o resultado é igual ao da letra .
Você pode substituir os dados na fórmula que vai encontrar a resposta também.
Resposta
(a)
(b) ; ;
(d)