Primeira Lei da Termodinâmica - Gases
Produzido por Leonardo de BemTeoria
Fala aí! Bem vindo ao RespondeAi, nessa página estaremos focados em buscar entender como a Primeira Lei da Termodinâmica influência a maneira que enxergamos os gases e como podemos estudar diferentes processos que podemos aplicar em um gás, como por exemplo aumentar sua temperatura, mudar o volume do compartimento em que ele está inserido, ou alterar a pressão sobre o gás.
A Primeira Lei da Termodinâmica trata da conservação de energia, ela diz que a energia nunca é criada nem destruída, ela sempre se transforma.
Isso permite que a gente estude transformações gasosas, muitos já estudaram isso no colégio, e chamavam de "piviti, povotó":
Mas na faculdade as mesma transformações são vistas, mas pensando na fórmula do trabalho de um gás.
O trabalho de um gás depende do seu volume inicial e final e da variação da pressão, conforme a fórmula:
Então vamos analisar os quatro processos de transformações gasosas que conhecemos analisando essa integral:
Processo Isobárico
Quando a pressão é constante temos a integral:
Logo o trabalho realizada por um gás em um processo isobárico pode ser calculado a partir da área de uma função
Processo Isovolumétrico
Quando o volume é constante,
E isso é até intuitivo, pense que para uma máquina térmica gerar trabalho, normalmente a expansão do gás movimenta um pistão que movimenta outras partes móveis, se o gás não altera seu volume, ele não se expande, e não é capaz de movimentar nada e por isso o trabalho dele é zero.
Processo Isotérmico
Quando a temperatura é constante, temos que pedir ajuda para Clapeyron, ou seja, para descrever a pressão em termos da temperatura, temos que usar a equação
Então nossa integral do trabalho ficaria:
Calculando essa integral, o trabalho em um processo isotérmico é:
Essas são as curvas isotérmicas que podem ser visas em um gráfico
Processo Adiabático
Em processos adiabáticos existem mudanças no gás mas sem que ele sofra variação de calor, ou seja, sem o gás perder o ganhar energia:
Pela Primeira Lei:
Logo:
Você pode entender como calcular a energia interna de um gás aqui: Energia Interna de Um Gás
No nosso conteúdo exclusivo para assinantes você encontra gráficos, vídeos, e muitos exercícios sobre diferentes processos termodinâmicos em gases ideais, acompanha aqui em baixo um de nossos exercícios resolvidos.
Exercício
Acompanhe a resolução de um exercício de um prova de física da UERJ:
Um gás ideal, inicialmente sob pressão
a) Qual e a pressão do gás após a expansão livre?
b) O gás, então, é lenta e adiabaticamente comprimido até seu volume original. A pressão após a compressão é de
Processo Isobárico
Processo Isovolumétrico
Processo Isotérmico
Processo Adiabático
Exercício
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 212. x-y 77
Uma amostra de gás se expande de uma pressão inicial de e um volume inicial de para um volume final de . Durante a expansão, a pressão e o volume estão relacionados pela equação , onde . Determine o trabalho realizado pelo gás durante a expansão.
Passo 1
Para calcularmos o trabalho realizado por um gás só temos uma fórmula a usar
Substituindo os valores de volume inicial e final e pela expressão que ele representa, temos
Resolvendo a integral temos
Resposta
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 241. x-y 12
No intervalo de temperatura de a , a pressão de um certo gás não ideal está relacionada ao volume e à temperatura através da equação
Qual é o trabalho realizado pelo gás se a temperatura aumenta de para enquanto a pressão permanece constante?
Passo 1
Temos que resolver a seguinte integral, certo?
Como o enunciado fala que a pressão permanece constante, então podemos colocar para fora da integral e ficamos com
Resolvendo a integral temos
Passo 2
Bom, agora precisamos descobrir quanto vale volume inicial e final, e faremos isso usando a equação que o enunciado forneceu
Para acha os valores do volume, vamos isolar o volume nessa equação
Substituindo agora o valor da temperatura inicial e final temos
Substituindo agora na fórmula de trabalho, chegamos em
Assim,
Resposta
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 241-13.
O ar inicialmente ocupa à pressão manométrica de se expande isotermicamente para uma pressão de e em seguida é resfriado a pressão constante até atingir o volume inicial. Calcule o trabalho realizado pelo ar. (Pressão manométrica é a diferença entre a pressão real e a pressão atmosférica)
Passo 1
Queremos calcular o trabalho realizado pelo ar. Para isso vamos dividir o processo em três estados.
Aqui tem uma pegadinha mega importante! A pressão que ele dá em A é a pressão manométrica! Logo pra saber a pressão exata em A temos que somar a pressão atmosférica () ao valor que ele deu! ;)
Estado – o inicio
Estado – o estado intermediário
Estado – o final
Passo 2
Agora que dividimos os estados, vamos calcular o trabalho realizado ao passar de e depois o trabalho de e soma-los
O processo realizado de é isotérmico, então temos que resolver a integral
Mas como ele é isotérmico, podemos achar uma função que descreva o comportamento da pressão, certo? Só lembrarmos da fórmula
Então
Substituindo na integral, temos
Resolvendo essa integral chegamos em
Como terminamos de ver que
Podemos substituir na equação por
Podemos usar a relação do “piviti-povoto” para um processo em que a temperatura não muda e temos que
Então
Substiuindo isso na fórmula do trabalho chegamos que
Substiuindo os dados que temos e lembrando que a pressão que foi dada é manométrica, devemos somar a pressão da atmosfera para podermos calcular, temos
Passo 3
Agora vamos calcular o trabalho no processo , como ele é um processo a pressão constante, temos que a integral é
Porém não sabemos o valor de , temos que encontra-lo antes de tudo para calcular o trabalho nesse processo
Por “piviti-povotó” já vimos que
Substituindo na equação do trabalho temos
Como
Colocando os valores agora temos
Passo 4
Agora basta somar com
Resposta
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2. Rio de Janeiro: LTC , 2008, 49
Quinhentos joules de trabalho devem ser realizados a fim de comprimir um gás à metade de seu volume inicial a temperatura constante. Quanto trabalho deverá ser realizado para comprimir o gás por um fator de , iniciando com o mesmo volume inicial?
Passo 1
Quando queremos determinar a variação do trabalho durante um processo isotérmico, devemos lembrar da seguinte relação:
Pelo enunciado do problema, temos que são necessários para que . Como é uma compressão o trabalho é negativo, ou seja, . Montando a equação, temos:
Agora que temos quanto vale , podemos determinar quanto de trabalho deve ser realizado sobre o gás para que ele seja comprimido por um fator de , se liga!
Passo 2
Voltando à equação do trabalho, temos:
Substituindo e , temos:
Resposta
Exercício Resolvido #5
UFRJ – 1ª Prova – 2012.2
Considere um gás ideal que absorve calor segundo um dos processos que seguem: a volume constante; a pressão constante e a temperatura constante. Para quais desses processos tem-se a variação da energia interna do gás igual a zero?
Apenas (i).
Apenas (ii).
Apenas (iii).
Apenas (i) e (ii).
Apenas (i) e (iii).
Apenas (ii) e (iii).
Todas elas.
Nenhuma delas.
Passo 1
Vamos ver um por um:
- A variação a volume constante, segundo a primeira lei, é dada por:
Como o volume se mantem constante, temos que:
Então:
Passo 2
- A pressão se mantendo constante, faz com que o trabalho seja dada por:
Então:
Passo 3
- Nesse caso, como a energia interna é uma função da temperatura, se a variação da temperatura é igual a zero, a variação da energia interna também é:
Resposta
Exercício Resolvido #6
UERJ – Lista para 2ª Prova
Um gás ideal, inicialmente sob pressão , sofre uma expansão livre (adiabática, sem trabalho externo) até que seu volume final seja vezes o seu volume inicial. Responda:
Qual é a pressão do gás após a expansão livre?
O gás, então, é lenta e adiabaticamente comprimido até seu volume original. A pressão após a compressão é de . Determine se o gás é monoatômico, diatômico ou poliatômico.
Passo 1
Primeiramente, vamos analisar uma expansão livre de acordo com a 1° lei da termodinâmica:
Como a expansão é livre, o gás não realizou trabalho, então:
Além disso, como a expansão ocorreu adiabaticamente, não houve troca de calor, então:
Logo:
Opa! Legal, chegamos à conclusão que a variação da energia interna é igual a . Mas isso nos ajuda em quê? Bem, a importância disso está no fato de que a energia interna é uma função da temperatura. Logo, se não houve variação da energia interna, não houve variação da temperatura! Logo:
Vamos lá então (:
Passo 2
Queremos saber a pressão após a expansão livre. Vamos usar o piviti-povotó:
Sabemos que:
Cortando na equação e substituindo :
Sendo :
Passo 3
Agora o gás é comprimido “lenta e adiabaticamente” até seu volume inicial. O que isso quer dizer? Quer dizer que podemos usar a equação:
Mas queremos descobrir que tipo de gás é esse. Mas como saberemos? Bom, o que nos dirá será o valor de :
Monoatômico:
Diatômico:
Caso o coeficiente não encaixe nesses casos, o gás será poliatômico!
Bom, sabemos que:
Aplicando na fórmula:
Simplificando:
Logo, o gás é poliatômico.
Resposta
Poliatômico
Exercício Resolvido #7
UFRJ – 1ª Prova – 2013.2
A figura abaixo mostra três possíveis expansões de um gás ideal monoatômico, que encontra-se inicialmente no estado (cujo volume é ) para os estados finais , ou , todos de volume , através de três processos reversíveis diferentes:
transformação isobárica;
transformação isotérmica
transformação adiabática
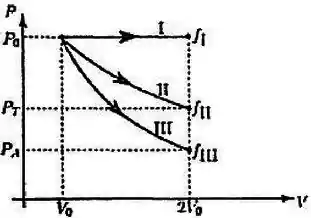
Sobre tais processos, é INCORRETO afirmar que:
A maior troca de calor se dá no processo isobárico.
O trabalho realizado pelo gás é menor no processo adiabático.
No processo isotérmico, todo o trabalho é transformado em calor.
As temperaturas finais terão a relação .
Na transformação isotérmica, não haverá calor trocado com o gás, uma vez que .
Passo 1
Vamos analisar, rapidamente, cada uma das alternativas:
Item : A maior troca de calor se dá no processo isobárico.
Olhando de cara, não dá pra saber se a maior troca de calor acontece nessa, mas, como o trabalho é área sob a curva, sabemos que:
Vamos pular esse por enquanto.
Passo 2
Item : O trabalho realizado pelo gás é menor no processo adiabático.
Essa é verdadeira, pois a curva adiabática corresponde à menor área, como acabamos de ver.
Passo 3
Item : No processo isotérmico, todo o trabalho é transformado em calor.
Essa também é verdadeira, pois, como o processo é isotérmico: .
Logo, , pois:
Então, pela Primeira Lei:
Por isso, é verdadeiro que todo o trabalho se converte em calor ou vice-versa.
Passo 4
Item : As temperaturas finais terão a relação .
Olhando de cara, também não fica tão claro. Vamos ver a próxima.
Passo 5
Item : Na transformação isotérmica, não haverá calor trocado com o gás, uma vez que .
Vimos que, na transformação isotérmica, .
Logo:
Então, a afirmativa é falsa!
Quando , e não !
Passo 6
Só para conferir, agora podemos verificar item :
Vimos que .
Além disso, .
Como a temperatura inicial é a mesma, então:
Como
Então:
Ora, se e :
Portanto, a maior troca de calor se dá no processo isobárico .
Verdadeira.
Passo 7
Conferindo item :
Podemos aplicar a equação dos gases ideais no estado final (piviti povotó).
Mas o volume é o mesmo nos três casos ().
Logo:
Então, se a temperatura aumenta, a pressão também aumenta à mesma proporção.
Como , então:
Então a afirmativa é verdadeira!
Resposta
Alternativa .
Exercício Resolvido #8
UERJ – Lista da 2ª Prova
Uma amostra de gás ideal se expande de uma pressão e volume iniciais de e para um volume final de .A temperatura inicial é . Se o gás for monoatômico e a expansão for isotérmica, quais são:
A pressão final,
A temperatura final, ?
O trabalho realizado pelo gás?
Refaça os itens anteriores para o caso em que a transformação é adiabática e o gás é monoatômico, e para o caso em que a transformação é adiabática e o gás é diatômico.
Dados:
-Constante dos Gases:
-Pressão atmosférica:
-Gás monoatômico:
Passo 1
Bom galera, nessa questão vamos usar vários conceitos de gases ideias. Essa questão é dividida em três casos:
-Caso 1: Se o gás for monoatômico e a expansão for isotérmica.
Nesse caso, as equações e constantes que vamos precisar usar são essas:
-Caso2: Se a transformação for adiabática e o gás for monoatômico:
As equações e constantes são:
-Caso3: Transformação é adiabática e o gás é diatômico.
As equações e constantes são:
Além do mais, sempre é bom lembrar da equação geral dos gases:
Bom, é isso! Mas não fique assustado, não vamos ter que refazer tudo em cada caso. Vamos fazer o primeiro caso e depois bastam algumas alterações nos outros dois (:
Passo 2
Vamos resolver os itens da questão para o caso 1 primeiro:
Temos que achar a pressão final. Lembrando que a transformação é isotérmica, ou seja, a temperatura final é igual a inicial, nossos dados são esses:
Vamos substituir esses dados na equação:
Vamos simplificar logo uma coisa: as temperaturas antes e depois são iguais, então podemos cortá-las da equação:
Queremos saber a temperatura final... Mas lembra que a transformação é isotérmica? Logo, a temperatura final é igual à inicial e vale:
Agora precisamos saber o trabalho que o gás realizou nessa transformação. A equação que usamos é a integral:
Mas como calcular isso se a pressão e o volume variam constantemente numa transformação isotérmica? Segue o gráfico dessa transformação:
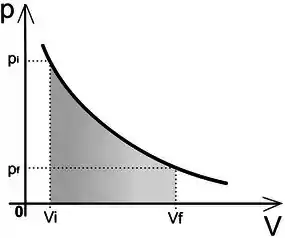
Bom, mas sabemos que a temperatura não varia! Vamos modificar essa integral para alguma que saibamos calcular. Usando a equação geral dos gases para isolar a pressão:
Substituindo na integral:
Notou o pulo do gato no final? Isso porque
Ótimo, pois temos o volume inicial e final. Substituindo na equação os valores e , , e convertendo as unidades:
Ufa! Vamos agora aos outros casos.
Passo 3
-Caso2:
Como agora estamos lidando com uma transformação adiabática, vamos usar:
Com:
Além disso, temos os mesmos valores iniciais para o estado que o passo anterior. Logo, aplicando os valores de pressão e volume que temos na equação, podemos encontrar a :
Eita, agora não podemos dizer que , pois a transformação não é isotérmica! Então a gente vai ter que apelar pro Piviti-Povóto:
Bom, precisamos calcular o trabalho realizado por um gás numa transformação adiabática! Como o gás é monoatômico, usaremos:
é fácil de ser obtido pois sabemos e :
E o pode ser obtido usando a equação geral dos gases e as condições iniciais(convertendo as unidades de pressão e volume):
Substituindo as duas quantidades na fórmula:
(:
Passo 4
-Caso3:
O caso 3 é bem similar ao caso 2. A única diferença é que o gás é diatômico. Sim, essa questão é um pouco repetitiva (u.u), mas ela nos ajuda a compreender as diferenças de cada transformação!
Vamos resolver o caso 3 mais rapidamente, lembrando-se de utilizar as mesmas condições de temperatura, volume e pressão iniciais que usamos nos outros:
Vamos usar, novamente, a equação:
Precisamos só recalcular o valor de para um gás diatômico:
Aplicando esse e os outros valores na equação:
Vamos usar de novo Piviti-Povotó pra achar a temperatura final:
Novamente, como a transformação é adiabática, podemos escrever:
Só que os gases diatômicos têm 5 graus de liberdade, como vimos na teoria, então:
O é fácil de calcular já que temos e :
E o pode ser obtido usando a equação geral dos gases e as condições iniciais (convertendo as unidades de pressão e volume):
Logo, substituindo na equação do trabalho:
Resposta
-Caso 1:
-Caso 2:
-Caso 3:
Exercício Resolvido #9
PUC-RIO – 3ª Prova – 2010.1
Um mol de gás ideal monoatômico, partindo sempre do estado inicial de volume , pressão e temperatura , dobra a temperatura por quatro processos diferentes. O processo é a volume constante, o processo é isobárico, o é linear com pressão final e é adiabático. Dê as respostas em função de , e .
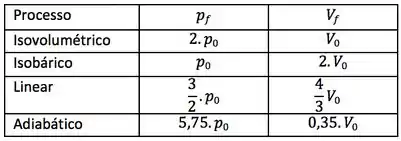
Coloque na tabela os valores da pressão e do volume no final de cada processo. Represente cada processo no diagrama .
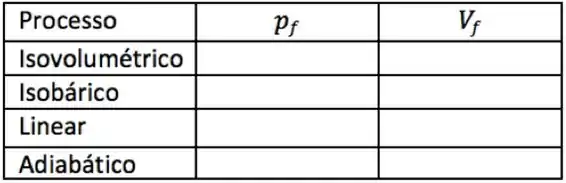
Calcule a variação da energia interna para cada um dos processos.
No processo , calcule o trabalho e o calor trocado.
Passo 1
Antes de atacar esse problema, vamos reunir as informações dadas:
Vamos primeiro analisar o processo :
Já sabemos que , vamos então descobrir , para isso, vamos usar a lei dos gases ideais, ao final do processo , temos:
Antes do processo ocorrer, temos:
dividindo a equação dado para o fim do processo pela equação antes do processo começar, temos:
Passo 2
Vamos agora para o processo , utilizaremos o mesmo processo, sabendo que a pressão permanece constante, precisamos apenas determinar o volume:
Ao fim do processo, temos:
Antes de o processo ocorrer, temos:
Dividindo as equeçoes, temos:
Passo 3
Para o processo , já sabemos o valor da pressão final, precisamos determinar o volume, vamos novamente utilizar o mesmo procedimento de antes:
Ao fim do processo, temos:
Antes de o processo ocorrer, temos:
Dividindo as equações, temos:
Passo 4
Agora vamos para o processo . Como se trata de um processo adiabático, teremos:
Para um gás ideal, temos que:
Voltando à equação para o processo, temos:
Agora só falta determinar a pressão, para isso, vamos fazer:
Agora é só montar a tabela e o diagrama:
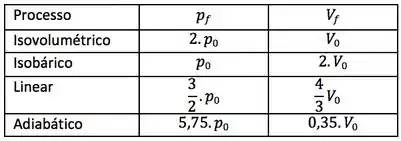
Para o diagrama, teremos:
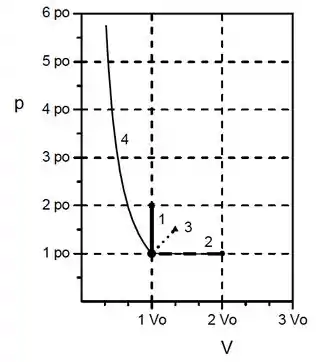
Passo 5
Para determinar a variação da energia interna, vamos relembra a sua definição para gases monoatômicos:
Como a variação de temperatura é a mesma em todos os processos, a variação da energia interna será a mesma em todos os processos:
Sabendo que:
Substituindo na equação da energia interna, temos:
Passo 6
Vamos analisar o processo . Mas primeiramente vamos reunir os dados pertinentes a esse processo:
Para determinar o trabalho, podemos calcular a área abaixo da curva do processo linear, podemos ver, pelo diagrama que se trata de um trapézio, portanto, temos:
Passo 7
Agora que temos o trabalho e a energia intera já calculados, podemos, pela primeira lei da termidinâmica calcular o calor trocado:
Resposta
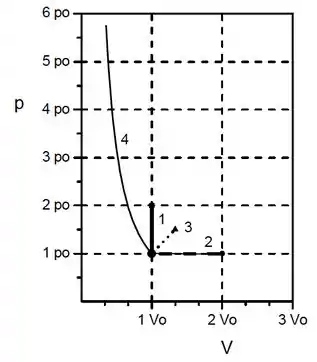
;