Primeira Lei da Termodinâmica em Ciclos
Teoria
O que são Ciclos?
Já sabemos calcular calor, trabalho e energia interna dos seguintes processos termodinâmicos: isobáricos, isométricos, isotérmicos e adiabáticos.
Beleza! Agora vamos considerar que esses processos ocorram de modo a fechar um ciclo.
Ou seja: as curvas de cada processo se encontram, delimitando uma área.
Por exemplo:
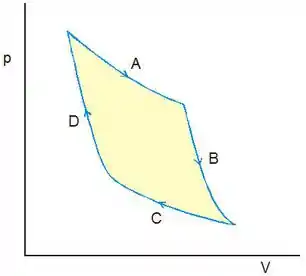
Nossa ideia é aplicar a Primeira Lei da Termodinâmica ao ciclo como um todo.
Bora fazer isso?
Primeira Lei em um ciclo
Aplicando a Primeira Lei em um ciclo fechado, temos o seguinte:
Mas sabemos que a energia interna é uma função de estado e só depende dos valores inicial e final.
Em um ciclo, esses valores são iguais!
Logo:
Esses valores são o saldo de calor e trabalho, respectivamente.
Estamos interessados no saldo de trabalho.
Podemos dizer que o saldo de calor é o que entra, ou seja o calor da fonte quente menos o que sai, calor rejeitado na fonte fria:
Substituindo:
Trabalho em um ciclo
O trabalho em um ciclo é exatamente a área do ciclo no diagrama .
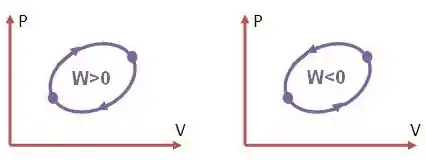
Se os processos estiverem em sentido horário:
Se os processos estiverem em sentido anti-horário:
Rendimento de um ciclo
O rendimento do ciclo vai ser o trabalho útil que ele produziu sobre o calor que ele recebeu. Ou seja:
Primeira Lei em um ciclo
Trabalho em um ciclo
Rendimento de um ciclo
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 209-46
Um sistema termodinâmico passa do estado para o estado , do estado para o estado e de volta para o estado , como mostra o diagrama da figura abaixo. A escala do eixo vertical é definida por , e a escala do eixo horizontal é definida por . Complete a tabela da figura abaixo introduzindo um sinal positivo, um sinal negativo ou um zero nas células indicadas. Qual é o trabalho líquido realizado pelo sistema em um ciclo ?
Passo 1
O problema nos pede para analisarmos os processos em separado e assim identificarmos o sinal de e
Para começar a estudar os processos, vamos primeiro descobrir a escala de cada eixo do gráfico, no eixo temos que então cada quadrado vale
E no eixo , então cada quadrado vale .
Agora vamos analisar o processo
Como é um processo em que há expansão (está aumentando), então
Pela primeira lei temos
Como
Então a soma de dois termos positivos dá necessariamente um termo positivo
Assim,
Vamos estudar agora o processo
Este processo é um processo a volume constante, então
Se trabalho é zero e o enunciado nos fornece que então pela primeira lei temos
Então
Agora, vamos estudar o processo
Como o volume diminui, temos que
Como temos um ciclo, temos que em a variação da energia interna é zero
Como a variação nos processos e são positivos, então para que a variação dê zero, então a variação de energia interna em tem que ser negativa
Agora para descobrir o sinal de , vamos analisar a primeira lei
Se e são negativas então é negativo
Então fica assim a tabela
Passo 2
O módulo do trabalho de um ciclo é a área interna do ciclo, então basta a gente calcular a área interna do triângulo.
Como sabemos o valor de cada quadrado podemos substituir:
Como terminamos de dizer:
Como o processo envolve um trabalho negativo com módulo maior que o do trabalho positivo envolvido no processo , o trabalho do ciclo deve ser negativo.
Logo:
Resposta
a, b, c, d, e, f, g)
h)
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 209. x-y 46
A figura abaixo mostra um ciclo fechado de um gás ( a figura não foi desenhada em escala). A variação da energia interna do gás ao passar de para ao longo da trajetória é Quando o gás passa de para recebe na forma de calor. Mais são recebidos quando o gás passa de para . Qual é o trabalho realizado sobre o gás quando ele passa de para ?
Passo 1
Primeiro, vamos lembrar que, pela primeira lei da termodinâmica, que nos demonstra a conservação da energia, temos:
Como em um ciclo a variação de energia interna é sempre nula, temos:
Passo 2
Beleza! Vamos, então, trabalhar com os dados do enunciado! Mas, antes disso, perceba que :
Ok! A primeira coisa que nos é dita é que e, então, com , vem:
, pois .
Passo 3
Agora, então, basta a gente trabalhar com a expressão anterior, pois o enunciado nos diz que e . Daí, temos:
e, então:
Opa, mas esse é o trabalho feito PELO gás. Como o problema quer o trabalho SOBRE o gás, só precisamos inverter esse sinal! Logo, nossa resposta será .
Resposta
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 210-49
Quando um sistema passa do estado para o ao longo da trajetória da figura abaixo, . . Ao longo da trajetória , .
Quanto vale ao longo da trajetória ?
Se na trajetória de retorno , quanto vale nessa trajetória?
Se , qual o valor de ?
Se , qual o valor de na trajetória ?
Se , qual o valor de na trajetória
Passo 1
Bom, como a variação da energia interna não depende do caminho, podemos escrever:
No percurso
Logo:
Passo 2
Novamente, a variação da energia interna não depende do caminho. No entanto, a variação da energia interna deve ser negativa em relação aos percursos que vão de pra Então:
Passo 3
A gente pode escrever:
Com:
Logo:
Passo 4
Tendo o valor da energia interna de e de , a gente pode calcular a variação da energia interna e aplicar a primeira lei entre os dois pontos. A gente sabe o trabalho realizado nesse percurso, então fica fácil calcular o calor no mesmo:
Logo:
Bom o trabalho ali é o mesmo trabalho do percurso , logo:
Passo 5
Vamos fazer a mesma coisa que antes:
Como (transformação isovolumétrica), a equação fica:
Resposta
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 211. x-y 50
Um gás em uma câmara passa pelo ciclo mostrado na figura abaixo . Determine a energia transferida pelo sistema na forma de calor durante o processo se a energia adicionada como calor durante o processo é , nenhuma energia é transferida como calor durante o processo e o trabalho líquido realizado durante o ciclo é .
Passo 1
É um exercício onde teremos que aplicar a primeira lei da temodinâmica em um ciclo para conseguirmos descobrir o que é pedido.
O problema nos fornece
Em um ciclo sabemos que
Assim
A transferência de calor no ciclo
É dada por
Como
Então
Resposta
Exercício Resolvido #5
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 213. x-y 93
Uma amostra de gás se expande de e para e seguindo a trajetória do diagrama da figura abaixo. Em seguida, o gás é comprimido de volta para , seguindo a trajetória ou a trajetória . Calcule o trabalho líquido realizado pelo gás para o ciclo completo ao longo da trajetória e da trajetória .
Passo 1
Sabemos que o trabalho de um ciclo é igual a área interna do ciclo. E se o sentido for horário é positivo se for anti-horário é negativo.
Então para calcular o trabalho do ciclo vamos fazer a área desse triângulo
Como o sentido é anti-horário o trabalho é negativo assim
Passo 2
Faremos o mesmo para o triangulo
Como o sentido é horário
Resposta
Exercício Resolvido #6
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2. Rio de Janeiro: LTC , 2008, 79
A figura representa um processo termodinâmico sofrido por de hélio.
Determine a pressão (em ), a temperatura (em ) e o volume (em ) do gás correspondentes aos pontos , e . Disponha seus resultados em uma tabela para facilitar a leitura.
Quanto trabalho é realizado sobre o gás durante cada um dos três segmentos mostrados na figura?
Quanto calor é transferido para o gás ou para fora dele durante cada um dos três segmentos?
Passo 1
Para resolver o item , vamos utilizar a famosa lei dos Gases Ideais:
Mas, precisamos primeiro determinar o número de mols envolvido!
Vamos agora reunir os dados que temos a respeito do ponto :
Portanto, precisamos determinar a temperatura , para isso, é só substituir na fórmula!
Vamos agora para o ponto ! Por se tratar de um processo isotérmico, temos que :
Agora é só substituir na fórmula para determinar a pressão , temos então:
Para o ponto , temos que ocorre um processo adiabático de para , desse modo, temos:
Isolando a pressão , que queremos determinar, temos:
Por se tratar de um gás monoatômico, temos:
Substituindo os dados, temos:
Para a temperatura , temos:
Dispondo os resultados em uma tabela, temos:
Passo 2
De para , por se tratar de um processo isotérmico, temos que a variação do trabalho é:
Substituindo os valores, temos:
De para , por se tratar de um processo isocórico, o trabalho é nulo!
De para , por se tratar de um processo adiabático, temos que a variação de trabalho é dada por:
Substituindo os valores, temos:
Passo 3
De para , por se tratar de um processo isotérmico, temos que a variação de energia interna é nula, portanto, temos:
De para , por se tratar de um processo isocórico, o trabalho é nulo, desse modo, temos:
De para , por se tratar de um processo adiabático, temos que:
Resposta
; ;
; ;