Segunda Lei da Termodinâmica e Entropia
Teoria
Fala aí, bem vindo ao RespondeAí! Nessa página vamos tratar da Segunda Lei da Termodinâmica e tentar entender as características da Entropia a partir da interpretação da segunda lei da termodinâmica.
Segunda Lei da Termodinâmica
Em Termodinâmica aprendemos sobre como mudanças de temperatura e o calor podem alterar o estado de um sistema de diversas formas diferentes, e a Segunda Lei da Termodinâmica, nos ensina que:
- Existem processos que acontecem em um único sentido e são irreversíveis, porque o calor é transferido espontaneamente do corpo com maior temperatura para o corpo de menor temperatura;
- Sempre existe perda de energia em forma de calor.
Essas são as duas principais características que definem a segunda lei da termodinâmica, e são utilizadas para derivarmos outros conceitos, como por exemplo a ideia de entropia.
Entropia
Mais importante que saber a definição de entropia, é saber do que ela se trata.
A entropia é uma variável de estado de um sistema. Essa variável tenta medir o nível de desordem do sistema, e pela tendência natural do calor de caminhar apenas em uma direção e gerar processos irreversíveis, podemos dizer que a entropia sempre aumenta com o tempo. Por isso dizemos que ela sempre é um valor que é positiva ou igual a zero.
Um bom exemplo para ter em mente é pensar em um sistema sendo aquecido, imagina que eu peguei um cubo de gelo, e aqueci ele até virar vapor, podemos dizer que houve um aumento da entropia desse sistema devido a adição de calor ao sistema.
Uma maneira de visualizar isso é pensar no modelo organizacional do sistema, conforme a figura:
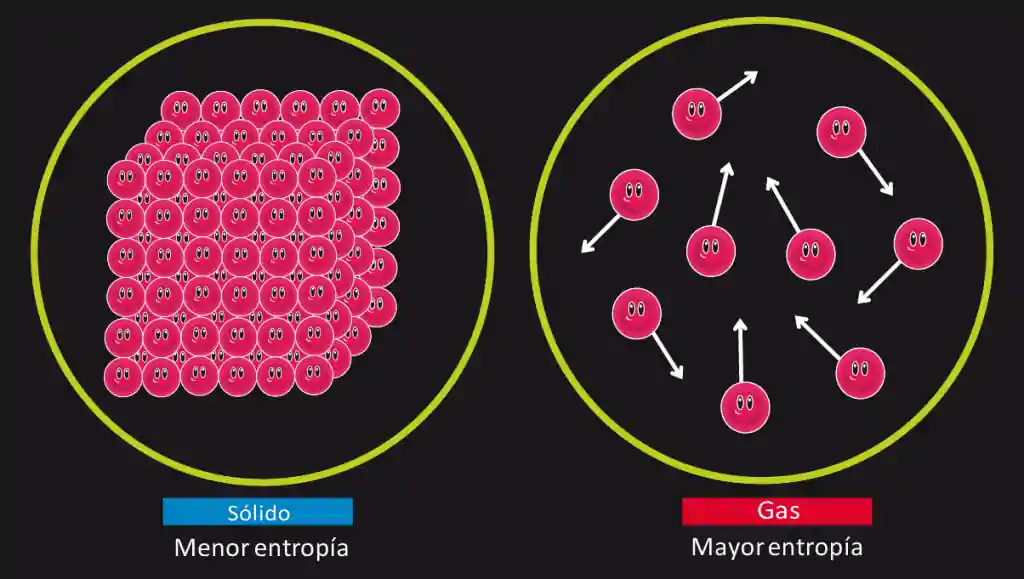
A variação de entropia do sistema, é uma função de estado e por isso não depende do caminho que o sistema tomou para chegar em certo estado, ou seja, só precisamos do valor do estado inicial e do valor do estado final do sistema para calcular a variação de entropia de um sistema.
Fórmulas
Quando falamos de Segunda Lei da Termodinâmica e de Entropia, tem algumas fómulas interessantes que devemos saber, como por exemplo, a fórmula de rendimento:
Sendo:
o rendimento o calor fornecido pela fonte de calor o calor não transformado em trabalho
Essa equação sempre vai ter como resultado um valor entre
E a fórmula de entropia:
E variação de entropia:
Exercícios
Acompanhe a resolução de um dos nossos exercícios de Segunda Lei da Termodinâmica e Entropia, feita pelos nossos Experts especialmente para você:
Em um experimento do laboratório, um cilindro de
Considere:
- Qual é a temperatura de equilíbrio?
- Quais são as variações de entropia do cilindro de alumínio, da água e do sistema alumínio-água?
Entropia
Fórmulas
Exercícios
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ – 1ª Prova – 2012.2
Um cubo de gelo de massa e calor latente de fusão funde-se à temperatura ambiente de um dia de verão no Rio de Janeiro. A temperatura do gelo é , constante durante a fusão. Qual a variação de entropia do gelo ao derreter-se? O resultado seria diferente se fosse inverno no Rio com temperatura ? O resultado seria diferente se o cubo derretesse fornecendo-lhe apenas trabalho?
. Não, pois a temperatura do gelo continua a mesma. Não, pois a entropia é uma função de estado.
. Não, pois a temperatura do gelo continua a mesma. Não, pois a entropia é uma função de estado.
. Sim, pois a temperatura externa é . Não, pois a entropia é uma função de estado.
. Não, pois a temperatura do gelo continua a mesma. Sim, pois a entropia depende da temperatura.
. Sim, pois a temperatura externa é . Sim, pois a entropia depende da temperatura.
Passo 1
Vamos primeiro calcular a variação de entropia do sistema. O gelo se funde a temperatura , e esssa que é a temperatura importante, pois o gelo é o sistema analisado, não o ambiente!.
Então:
Na fusão a temperatura é mantida constante durante todo o processo. Então podemos tirar a temperatura de integral, que fica:
E quem é esse calor? É o calor trocado durante uma fusão, ou seja, um calor latente de fusão.
Então:
Passo 2
A segunda pergunta é se aconteceria algo de diferente se a temperatura do ambiente fosse , no inverno.
A resposta é não, pois, como eu disse, o que importa no cálculo de entropia é a temperatura do sistema, que no caso é o gelo, e esse vai continuar tendo a mesma temperatura de fusão.
Passo 3
E por ultimo temos a pergunta se algo de diferente iria acontecer se fosse fornecido só trabalho.
Bem, quando se trata de variações de entropia, energia interna ou outra variável de estado, não importa o caminho que se escolha e sim os estados inicias e finais.
Isso é, não importa se fornecemos calor ou trabalho, só um dos dois ou apenas um dos dois, o que importa são as condições finais e inicias.
Como a questão não fala de uma alteração desses estados, a resposta é não!
Então a resposta é:
Alternativa
Resposta
Alternativa
Exercício Resolvido #2
UFRJ – 1ª Prova – 2013.2
Colocamos uma forma cheia d’água à temperatura ambiente dentro do congelador, que está a uma temperatura .
Considere as seguintes afirmativas sobre tal processo:
- O equilíbrio térmico será necessariamente atingido a .
- Neste caso, o congelamento da água é um processo irreversível.
- Durante a transição de fase, a temperatura da água não vai variar.
As afirmativas CORRETAS são:
Apenas I.
Apenas II.
Apenas III.
Apenas I e II.
Apenas I e III.
Apenas II e III.
Passo 1
Vamos analisar as afirmativas:
Afirmativa I: O equilíbrio térmico será necessariamente atingido a .
Falso, pois a água, após congelar a , pode baixar sua temperatura até , permanecendo em equilíbrio térmico com o congelador.
Passo 2
Afirmativa II: Neste caso, o congelamento da água é um processo irreversível.
Para saber isso, vamos analisar a variação de entropia total:
Nesse caso, o sistema é a água e a vizinhança é o congelador.
Sabemos, pela conservação de energia, que o calor perdido pela água é absorvido pelo congelador:
Mas a temperatura da água no congelamento é e a temperatura do congelador é .
Logo:
Substituindo:
Substituindo :
Como a água perde calor, então .
E como , então:
Logo:
Então o processo é irreversível!
Afirmativa verdadeira.
Passo 3
Afirmativa III: Durante a transição de fase, a temperatura da água não vai variar.
Sabemos que, na mudança de fase, não há variação de temperatura (calor latente).
Portanto, a afirmativa é verdadeira.
Resposta
Alternativa .
Exercício Resolvido #3
PUC-RIO – 3ª Prova – 2012.1
Em um experimento do laboratório, um cilindro de de alumínio a é colocado em contato térmico com de água a dentro de um calorímetro (considere o calorímetro ideal, isto é, capacidade térmica nula e isolamento perfeito.)
Considere: ;
Qual é a temperatura de equilíbrio?
Quais são as variações de entropia do cilindro de alumínio, da água e do sistema alumínio-água?
Passo 1
Quando temos esse tipo de problema, envolvendo corpos em contato, devemos logo pensar em troca de calor! E quando se trata de um sistema isolado devemos ter em mente a conservação da energia!
Como queremos calcular a temperatura de equilíbrio do sistema, devemos sempre lembrar do cáculo do calor cedido ou recebido por um corpo. No nosso caso, teremos de acordo com a conservação da energia:
Passo 2
Vamos primeiro calcular :
Ou seja:
simplificando:
Passo 3
Vamos agora calcular :
Simplificando, temos:
Ahhh...sempre fique de olho para ver se está tudo com as mesma unidades!
Passo 4
Agora que já temos e , é só utilizar a fórmula da conservação da energia!
Isolando , temos:
Ahh..como o nosso calor específico foi dado em , obtivemos a temperatura em graus Celsius!
Além disso, como a variação de temperatura é a mesma tanto em graus Celsius quanto em Kelvin, podemos usar a variação em graus Celsius.
Passo 5
Agora precisamos calcular a variação da entropia. Para isso vamos recordar da definição de entropia:
Sabendo que:
Temos para a entropia:
Passo 6
Agora que temos a entropia em termos de valores conhecidos, podemos achar a variação da entropia para cada um dos componentes, começando pelo cilindro de alumínio:
Passo 7
Agora vamos calcular a variação de entropia da água, do mesmo modo que calculamos a do alumínio:
Passo 8
Para o sistema alumínuo-água, temos:
Resposta
Exercício Resolvido #4
UFRJ – 1ª Prova – 2014.1
Considere as seguintes afirmativas:
A variação da entropia de um sistema não depende da reversibilidade do processo termodinâmico mas a variação do conjunto sistema + vizinhança depende.
A variação da entropia de um sistema durante um processo reversível é oposta à variação da entropia da vizinhança. No entanto, durante um processo irreversível, um aumento da entropia do sistema é superior, em amplitude, à diminuição da entropia da vizinhança.
O desequilíbrio entre a variação da entropia de um sistema e de sua vizinhança durante um processo irreversível é devido a uma dissipação de energia que não pode mais ser usada para efetuar um trabalho. Não havendo dissipação durante um processo reversível, ele não resulta em um aumento da entropia do universo.
São verdadeiras:
Apenas .
Apenas .
Apenas .
Apenas e .
Apenas e .
Apenas e .
Todas.
Nenhuma.
Passo 1
Vamos analisar cada uma das afirmativas.
Afirmativa :
Primeira parte: “A variação da entropia de um sistema não depende da reversibilidade do processo termodinâmico”.
É verdade, pois a entropia é uma função de estado e não depende do caminho. Então, a variação de entropia entre dois estados é a mesma para qualquer processo entre esses dois estados, podendo ser reversível ou irreversível.
Segunda parte: “mas a variação do conjunto sistema + vizinhança depende”.
Sabemos que a variação de entropia do conjunto sistema + vizinhança (universo) revela se o processo é reversível ou irreversível, isto é:
processo irreversível
processo reversível
Então, a variação do conjunto sistema + vizinhança realmente depende se o processo é reversível ou irreversível.
Logo, afirmativa é verdadeira.
Passo 2
Afirmativa :
Primeira parte: “A variação da entropia de um sistema durante um processo reversível é oposta à variação da entropia da vizinhança”.
Verdadeiro, pois sabemos que a variação de entropia total (ou do universo) é zero em processos reversíveis.
Logo:
Se :
Segunda parte: “No entanto, durante um processo irreversível, um aumento da entropia do sistema é superior, em amplitude, à diminuição da entropia da vizinhança”.
Também é verdade.
Em processos irreversíveis:
Logo:
Se (diminuição de entropia da vizinhança), então tem que ser maior, em módulo (amplitude), para que a soma seja maior que zero!
Afirmativa verdadeira.
Passo 3
Afirmativa :
Primeira parte: “O desequilíbrio entre a variação da entropia de um sistema e de sua vizinhança durante um processo irreversível é devido a uma dissipação de energia que não pode mais ser usada para efetuar um trabalho”.
Um processo irreversível é caracterizado por uma perda de energia em forma de calor.
Essa “perda” significa que a energia não pode ser aproveitada, isto é, não pode ser transformada em energia útil, como trabalho.
Portanto, a afirmativa está correta.
Segunda parte: “Não havendo dissipação durante um processo reversível, ele não resulta em um aumento da entropia do universo”.
A variação da entropia do universo ser zero caracteriza processos reversíveis:
processo reversível.
Correto.
Então, a afirmativa também está correta.
Logo, todas são verdadeiras!
Resposta
Alternativa .
Exercício Resolvido #5
UERJ – Lista para 2ª Prova
Um cubo de gelo de a é colocado em um lago cuja temperatura é de . “Calcule a variação na entropia do sistema cubo-lago quando o cubo de gelo atingir o equilíbrio térmico com o lago”. O calor específico do gelo (Sugestão: O gelo afetará a temperatura do lago?).
Dados:
- calor específico do gelo .
-calor específico da água = .
- calor latente de fusão do gelo = .
Passo 1
Bom galera, nessa questão nós estamos interessados em saber a variação total de entropia de um sistema, no caso, o sistema gelo-lago. Se liga ai então nas equações que vamos usar:
- Variação de entropia:
- Quantidade de calor:
- Calor Latente:
É isso! Mas antes de começarmos, temos que dar atenção a algumas informações importantes do enunciado:
- : A temperatura do lago não muda. Isso acontece porque o lago é um corpo muito mais massivo que o cubinho de gelo.
- : O cubo de gelo começa sólido, passa por um processo de fusão e depois, como água, se aquece até (Já que a temperatura do lago não muda e eles precisam atingir o equilíbrio térmico).
Obs.: Vamos usar as constantes que estão em unidades do .Isso facilita a no final das contas ;D.
Partiu resolver essa questão, então! (:
Passo 2
Vamos focar nossa atenção primeiramente no cubo de gelo:
Bom, já sabemos que o cubo vai passar por três “estágios”: Gelo, fusão e água. Vamos calcular a variação de entropia de cada um?
Primeiramente o gelo está sendo aquecido pelo lago. A variação de entropia do gelo vai ser dada por:
Só que, no caso, vale:
Logo:
O gelo é aquecido até , então essas são sua temperatura inicial e final. Convertendo essas temperaturas pra Kelvin e substituindo na equação, teremos:
Bom, no segundo estágio o gelo é fundido. Esse processo acontece à temperatura constante e o calor trocado é o calor latente. Logo:
E no terceiro estágio, parecido com o primeiro, o cubo que agora é feito de água é aquecido de até .A fórmula da variação de entropia é parecida com a do primeiro estágio, mudando apenas o calor específico:
Com as temperaturas em Kelvin:
Logo, a variação de entropia será:
Pronto! Agora, pra descobrirmos a variação total de entropia do bloco, basta somarmos as parcelas:
Passo 3
Vamos nos concentrar no lago agora. Bom, o caso do lago é mais fácil. A sua temperatura não muda com o processo, então a variação de entropia dele será:
A temperatura do lago vale , então .
Mas quanto vale ? Bom, a primeira lei, a conservação da energia, é respeitada nessa questão, já que nada que contraria isso foi dito. Então, esse calor tem que ser o calor que foi perdido para o cubo de gelo!
Bom, vamos calcular essa quantidade de calor para cada estágio que o cubo passou (lembrando que temos que colocar o sinal de menos no fim, já que o lago perde calor):
Logo, ,a quantidade de calor que o lago perdeu, vale:
Então a variação de entropia será:
Passo 4
Agora que temos as variações de entropia do cubo e do lago, podemos calcular a variação total do sistema cubo-lago. Calcular a variação de entropia de um sistema é fácil, basta somarmos a variação de cada parte do sistema. Então:
E essa é a resposta! Uma dica pra gente checar se a resposta não está errada é lembrar que sempre temos: