Exercícios de Variação da Entropia e Segunda Lei da Termodinâmica - Lista de Exercícios Resolvida

Considere as seguintes afirmativas:

A variação da entropia de um sistema não depende da reversibilidade do processo termodinâmico mas a variação do conjunto sistema + vizinhança depende.

A variação da entropia de um sistema durante um processo reversível é oposta à variação da entropia da vizinhança. No entanto, durante um processo irreversível, um aumento da entropia do sistema é superior, em amplitude, à diminuição da entropia da vizinhança.

O desequilíbrio entre a variação da entropia de um sistema e de sua vizinhança durante um processo irreversível é devido a uma dissipação de energia que não pode mais ser usada para efetuar um trabalho. Não havendo dissipação durante um processo reversível, ele não resulta em um aumento da entropia do universo.

São verdadeiras:

Apenas .

Apenas .

Apenas .

Apenas e .

Apenas e .

Apenas e .

Todas.

Nenhuma.

Um cubo de gelo de massa e calor latente de fusão funde-se à temperatura ambiente de um dia de verão no Rio de Janeiro. A temperatura do gelo é , constante durante a fusão. Qual a variação de entropia do gelo ao derreter-se? O resultado seria diferente se fosse inverno no Rio com temperatura ? O resultado seria diferente se o cubo derretesse fornecendo-lhe apenas trabalho?

. Não, pois a temperatura do gelo continua a mesma. Não, pois a entropia é uma função de estado.

. Não, pois a temperatura do gelo continua a mesma. Não, pois a entropia é uma função de estado.

. Sim, pois a temperatura externa é . Não, pois a entropia é uma função de estado.

. Não, pois a temperatura do gelo continua a mesma. Sim, pois a entropia depende da temperatura.

. Sim, pois a temperatura externa é . Sim, pois a entropia depende da temperatura.

Um cubo de gelo de a é colocado em um lago cuja temperatura é de . “Calcule a variação na entropia do sistema cubo-lago quando o cubo de gelo atingir o equilíbrio térmico com o lago”. O calor específico do gelo (Sugestão: O gelo afetará a temperatura do lago?).

Dados:

- calor específico do gelo .

-calor específico da água = .

- calor latente de fusão do gelo = .

Em um experimento do laboratório, um cilindro de de alumínio a é colocado em contato térmico com de água a dentro de um calorímetro (considere o calorímetro ideal, isto é, capacidade térmica nula e isolamento perfeito.)

Considere: ;

Qual é a temperatura de equilíbrio?

Quais são as variações de entropia do cilindro de alumínio, da água e do sistema alumínio-água?

Colocamos uma forma cheia d’água à temperatura ambiente dentro do congelador, que está a uma temperatura .

Considere as seguintes afirmativas sobre tal processo:

1. O equilíbrio térmico será necessariamente atingido a .
2. Neste caso, o congelamento da água é um processo irreversível.
3. Durante a transição de fase, a temperatura da água não vai variar.

As afirmativas CORRETAS são:

Apenas I.

Apenas II.

Apenas III.

Apenas I e II.

Apenas I e III.

Apenas II e III.

Em um experimento do laboratório, um cilindro de de alumínio a é colocado em contato térmico com de água a dentro de um calorímetro (considere o calorímetro ideal, isto é, capacidade térmica nula e isolamento perfeito.)

Considere: ;

Qual é a temperatura de equilíbrio?

Quais são as variações de entropia do cilindro de alumínio, da água e do sistema alumínio-água?

1. Calcule a massa de vapor d’água a que precisa ser misturada com de gelo a , para produzir água a .
2. Calcule a variação de entropia total do sistema durante esse processo.
3. Esse processo é reversível ou irreversível. Baseando-se na 2ª Lei da Termodinâmica, comente se isso está de acordo com sua resposta do item (b).

Considere o ciclo de Stirling, funcionando como refrigerador, para o qual as etapas são isotérmicas e as etapas são isovolumétricas. São conhecidas as temperaturas máximas e mínima e o razão entre o maior e o menor volume. Suponha que a substância de trabalho é um gás ideal com n moles e capacidade térmica molar a volume constante

(a) Esboce o diagrama correspondente a este ciclo, deixando claro cada uma das etapas.

(b) Determine o calor trocado e o trabalho realizado pelo gás em cada um dos quatro processos do ciclo.

(c) Qual a variação da entropia em cada ciclo?

Um dado sistema sofre um processo termodinâmico entre os estados de equilíbrio térmico e . Conhecendo-se um processo reversível que liga estes mesmos estados, podemos dizer que para o processo , sempre é possível calcular:

1. , o trabalho realizado pelo sistema e .
2. , , o calor absorvido pelo sistema e , pois são grandezas relacionadas pela e lei.
3. , e .
4. A variação de entropia e a variação de energia interna , pois e são funções de estado.
5. e .

Um cubo de gelo de massa e calor latente de fusão funde-se à temperatura ambiente de um dia de verão do Rio de Janeiro. A temperatura do gelo é , constante durante a fusão. Qual a variação de entropia do gelo ao derreter-se? O resultado seria diferente se fosse inverno no rio com temperatura O resultado seria diferente se o cubo derrete-se fornecendo-lhe apenas trabalho?

1. . Não, pois a temperatura do gelo continua a mesma. Não, pois a entropia é uma função de estado.
2. . Não, pois a temperatura do gelo continua a mesma. Não, pois a entropia é uma função de estado.
3. . Sim, pois a temperatura externa é. Não, pois a entropia é uma função de estado.
4. . Não, pois a temperatura do gelo continua a mesma. Sim, pois a entropia depende da temperatura.
5. . Sim, pois a temperatura externa é. Sim, pois a entropia depende da temperatura.

Considere um recipiente de paredes adiabáticas, dividido ao meio por uma membrana também adiabática.

No começo, um lado do recipiente contém um gás com capacidade térmica a temperatura , e o outro lado contém um gás com capacidade térmica a temperatura .

Quando a membrana é substituída por outra condutora térmica, os gases trocam calor até atingirem a temperatura de equilíbrio . Considere .

Calcule, em termos de , ,, , a temperatura de equilíbrio e a variação de entropia do sistema.

1. ,
2. ,
3. ,
4. ,
5. ,

Colocamos uma forma cheia d’água à temperatura ambiente dentro do congelador, que está a uma temperatura .

Considere as seguintes afirmativas sobre tal processo:

1. O equilíbrio térmico será necessariamente atingido a .
2. Neste caso, o congelamento da água é um processo irreversível.
3. Durante a transição de fase, a temperatura da água não vai variar.

As afirmativas CORRETAS são:

1. Apenas I.
2. Apenas II.
3. Apenas III.
4. Apenas I e II.
5. Apenas I e III.
6. Apenas II e III.

Uma certa quantidade de massa de uma substância que se vaporiza à temperatura e tem calor latente de vaporização pode ser completamente vaporizada por dois processos: (i) em contato com um reservatório térmico a temperatura ; (ii) em contato com um reservatório térmico a temperatura . Considerando-se apenas o processo de vaporização da substância nos processos (i) e (ii), pode-se afirmar que os mesmos são respectivamente:

1. Reversível, reversível.
2. Reversível, irreversível.
3. Irreversível, reversível.
4. Irreversível, irreversível.
5. Nada se pode afirmar.

Um cubo de gelo de massa e calor latente de fusão funde-se à temperatura ambiente de um dia de verão no Rio de Janeiro. A temperatura do gelo é , constante durante a fusão. Qual a variação de entropia do gelo ao derreter-se? O resultado seria diferente se fosse inverso no Rio com temperatura ? O resultado seria diferente se o cubo derretesse fornecendo-lhe apenas trabalho?

1. . Não, pois a temperatura do gelo continua a mesma. Não, pois a entropia é uma função de estado.
2. . Não, pois a temperatura do gelo continua a mesma. Não, pois a entropia é uma função de estado.
3. . Sim, pois a temperatura externa é . Não, pois a entropia é uma função de estado.
4. . Não, pois a temperatura do gelo continua a mesma. Sim, pois a entropia depende da temperatura.
5. . Sim, pois a temperatura externa é . Sim, pois a entropia depende da temperatura.

Um gás ideal está confinado dentro de um cilindro com um pistão móvel. O pistão é empurrado lentamente para dentro de uma maneira que a temperatura do gás permanece constante a 20°C. Durante a compressão, 730 J de trabalho é feito sobre o gás.

1. Qual é a variação na entropia do gás?
2. Explique porque o resultado do item anterior não viola a segunda lei da termodinâmica

Um corpo A, de massa m e calor específico c, a uma temperatura inicial TA troca calor com um reservatório térmico R a temperatura fixa TR, sem realizar ou sofrer trabalho. Se A muda sua temperatura para T’A, as variações de entropia em A, ∆SR são dadas por

(a) .

(b)

(c)

(d)

(e)

Um recipiente de paredes rígidas e adiabáticas e com capacidade térmica desprezível contém moles de um sal de capacidade térmica molar a volume constante dada por , onde é uma constante e a temperatura. Inicialmente, o sal está em equilíbrio térmico à temperatura . Troca-se, então, uma das paredes adiabáticas do recipiente por uma diatérmica e coloca-se o sistema em contato térmico com um reservatório a temperatura . Observa-se que após algum tempo o sal e o reservatório atingem o equilíbrio térmico. Calcule, neste processo e apenas em termos dos dados do problema.

1. O calor total fornecido pelo reservatório ao sal.
2. As variações de entropia do reservatório e do sal.
3. A variação da entropia do universo.

Considere as três afirmativas abaixo, a respeito de processos IRREVERSÍVEIS sofridos por um sistema:

1. Em geral, não podemos dizer nada sobre o trabalho sofrido pelo sistema.
2. A entropia de pelo menos uma parte do sistema necessariamente aumentará.
3. Se este processo também for adiabático, a variação de entropia será zero.

Marque a alternativa que indica as afirmativas CORRETAS:

1. I
2. II
3. III
4. I e II
5. I e III
6. II e III
7. Todas estão corretas.
8. Nenhuma está correta

Um fabricante anuncia uma máquina recém-desenvolvida que, em cada ciclo, retira 100 J de um reservatório com água fervente a 100 °C, realiza 80 J de trabalho e rejeita 20 J de calor em outro reservatório mantido a 10 °C. Existe algo de errado neste anúncio?

a) De acordo com a Segunda Lei da Termodinâmica, o calor rejeitado sempre deve ser maior que o trabalho útil.

b) A Primeira Lei da Termodinâmica é violada porque 100 J + 20 J ≠ 80 J.

c) Em um ciclo, a máquina térmica deveria retirar calor do reservatório a 10 ºC e rejeitar calor para o reservatório a 100 ºC.

d) A eficiência desse ciclo excede o limite superior estabelecido pela Segunda Lei da Termodinâmica.

e) Não há nada de errado neste anúncio, pois 100 J = 20 J + 80 J.

É possível transferir calor de um reservatório frio para um reservatório quente?

A) Não, pois viola a segunda lei da termodinâmica.

B) Sim, isso acontecerá naturalmente.

C) Sim, mas trabalho terá que ser realizado.

D) Não, pois viola a primeira e segunda leis da termodinâmica.

E) Não, pois viola a primeira lei da termodinâmica

Qual dos seguintes exemplos representa um processo reversível?

a) A colisão de um carro com um caminhão.

b) Uma dinamite explodindo.

c) As colisões das moléculas em uma gás.

d) Abrir a válvula de um tanque de ar pressurizado a temperatura ambiente até que a pressão do tanque se iguale à pressão ambiente.

e) Aquecer com uma chama água que está inicialmente à temperatura ambiente até ela começar a ferver.

Em um recipiente isolante térmico, que continha de uma mistura de gelo e água, em equilíbrio térmico, foi colocado um bloco de de cobre à temperatura de . O conjunto atinge novamente o equilíbrio à temperatura de .

Dados:

, , .

a) Quanto calor é cedido pelo bloco de cobre neste processo?

b) Quanto calor é absorvido pela água neste processo?

c) Quanto de gelo estava no balde, antes do bloco de cobre ser colocado nele?

d) Determine a variação de entropia do sistema água-gelo-cobre neste processo. Este processo é reversível ou irreversível?

Sejam e as variações da energia interna e da entropia de um mol de um gás ideal ao realizar uma expansão adiabática livre à temperatura , dobrando seu volume. Sejam e as variações da energia interna e da entropia da mesma quantidade de gás ideal ao realizar uma transformação isotérmica reversível à temperatura , também dobrando seu volume. Podemos afirmar que:

(a)

(b)

(c)

(d)

1. Um tacho com capacidade térmica desprezível contém de água a . Um cilindro de cobre de , muito quente, é jogado na água, fazendo a água ferver e transformando da água em vapor. O processo ocorre a pressão atmosférica. A temperatura final do sistema é de . Despreze a transferência de calor para o ambiente.
1. Qual é a energia transferida para a água na forma de calor?
2. Qual é a temperatura inicial do cilindro?
3. Calcule a variação de entropia total do sistema durante esse processo.
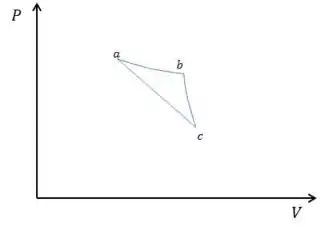
2. No diagrama abaixo, o gás realiza de trabalho quando percorre a isoterma e quando percorre a adiabática . Calcule a variação de energia interna do gás quando percorre a trajetória retilínea

Dados:

Um bloco de um certo material de massa à temperatura é colocado dentro de uma caixa isolada junto com um bloco a temperatura de massa . Sabendo que o calor específico do segundo bloco é o dobro do calor específico do primeiro, analise as seguintes afirmativas:

(I) A temperatura de equilíbrio do sistema é igual a . (II) A variação de energia interna do sistema é diferente de zero. (III) A variação de energia interna do sistema é nula. (IV) A entropia do sistema aumenta. (V) A entropia do sistema diminui.

São verdadeiras:

1. I, III e IV
2. I, II e V
3. III e V
4. II e V
5. Apenas II
6. Apenas I

Um gás ideal é levado de uma temperatura inicial Ti a uma temperatura final maior Tf ao longo de duas trajetórias reversíveis. A trajetória A é a pressão constante e a trajetória B é a volume constante. Qual é a relação entre as variações de entropia do gás para essas trajetórias?

a) ;

b) ;

c) ;

d) apenas se a temperatura inicial for baixa;

e) apenas se a temperatura inicial for elevada;

Considere um cilindro oco de material isolante com raio da parede interna 0,3 m. Sobre uma de suas extremidades é apoiado um disco fino de alumínio de massa 1 kg com raio de 0,301 m (considere-o bidimensional). O disco se encontra à temperatura de 150° C e é colocado em contato com gelo a 0° C. (Coeficiente de dilatação linear: ; despreze variações de temperatura do cilindro.) Determine:

a) A variação de temperatura que o disco deve sofrer para que se encaixe no tubo.

b) A quantidade de gelo que é preciso colocar em contato com o disco para que este sofra a variação de temperatura calculada no item a).

c) A variação de entropia do sistema gelo+disco até o momento do encaixe.

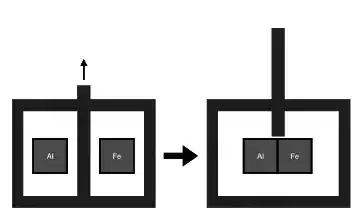
A figura ao lado mostra um bloco de alumínio de massa 1 kg e um bloco de ferro de massa 2 kg. A temperatura do bloco de alumínio é 300 K enquanto a temperatura do bloco de ferro é 500 K. Os blocos estão em uma caixa isolada termicamente e estão separados por uma divisória isolante. Quando removemos a divisória, depois de algum tempo, os blocos atingem a temperatura de equilíbrio. O calor específico do alumínio é = 900 J/kgK e o calor específico do ferro é = 450 J/kgK.

a) Qual a temperatura de equilíbrio?

b) Sem realizar cálculos, responda: A variação de entropia do sistema “bloco de alumínio + bloco de ferro" é positiva, negativa ou nula? Justifique sua resposta.

c) Qual é a variação de entropia do sistema “bloco de alumínio + bloco de ferro"? (sua resposta pode ficar em termos de frações simplificadas)

Um cubo de gelo a é colocado em uma banheira muito grande cheia com água a e derrete sem causar uma mudança apreciável na temperatura da água da banheira. Quais das seguintes afirmações é verdadeira?

1. A entropia ganha pelo cubo de gelo é igual a entropia perdida pela água.
2. A entropia perdida pelo cubo de gelo é igual a entropia ganha pela água.
3. A mudança total de entropia do sistema (cubo de gelo + água) é zero porque nenhum calor foi adicionado.
4. A entropia do sistema (cubo de gelo + água) aumenta porque o processo é irreversível.
5. A entropia da água não muda porque sua temperatura não mudou.

Um bloco de cobre de temperatura e massa é colocado em contato com um bloco de chumbo de massa a uma temperatura de dentro de uma caixa isolada. Assuma que o calor específico do cobre é dado por e que o calor específico do chumbo é

1. Calcule a temperatura de equilíbrio.
2. Determine quanta energia flui do bloco mais quente para o mais frio até que o equilíbrio seja atingido.
3. Calcule a variação de entropia do sistema fechado.

Se necessário use

Duas amostras de água são misturadas à pressão constante dentro de um recipiente adiabático: de água à e de água à . Sobre esse sistema são feitas as seguintes afirmativas:

I - Como o recipiente é adiabático, não há troca de calor entre o interior e o exterior do recipiente.

II - A quantidade de calor que a água morna cede é igual a quantidade de calor que a água fria recebe.

III - A variação de entropia do Universo é zero para esse processo.

São verdadeiras:

1. Somente a I.
2. Somente II e III.
3. Somente I e II.
4. Somente I e III.
5. Todas.

Que quantidade de calor é necessário fornecer para transformar um bloco de gramas de gelo a em água a ? Qual a variação da entropia neste processo?

Uma pedra de massa cujo calor específico é encontra-se inicialmente a uma temperatura . A pedra é colocada dentro de um calorímetro (de paredes adiabáticas e fixas) com capacidade térmica contendo uma quantidade de água de massa cujo calor específico é . A água e o calorímetro encontram-se inicialmente à temperatura tal que

. Após algum tempo, a pedra, a água e o calorímetro atingem o equilíbrio termodinâmico numa temperatura .Despreze as variações de e com a temperatura.

1. Calcule o calor RECEBIDO por cada um dos 3 corpos.
2. Determine como função de , , , , , e .
3. Calcule a variação de entropia para cada um dos 3 corpos, DESCREVENDO OS PROCESSOS TERMODINÂMICOS ENVOLVIDOS NOS CÁLCULOS. Calcule a variação de entropia do sistema isolado formado por pedra+calorímetro+água. Esta variação de entropia deve ser maior, menor ou igual a zero? JUSTIFIQUE.

Uma amostra isolada termicamente de um gás ideal a uma temperatura fixa é confinada à metade de um recipiente por uma membrana impermeável. A outra metade do contêiner está em vácuo. A membrana é então perfurada e é permitido ao gás expandir-se livremente e dobrar seu volume como mostrado. Qual das seguintes afirmações é verdadeira em relação a essa situação?

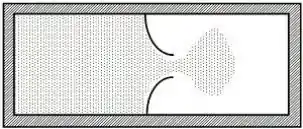
A) O processo é reversível

B) Este é um processo isotérmico

C) A entropia do gás diminui

D) A energia interna do gás deve diminuir

E) A temperatura do gás diminui para metade do seu valor original

Considere as seguintes afirmações:

1. Podemos sempre expressar a energia interna de um gás de uma substância qualquer num dado estado termodinâmico em função de sua temperatura e de sua pressão, .
2. Em qualquer processo adiabático o calor trocado é nulo e, consequentemente, a variação da entropia é zero.
3. As moléculas de duas amostras de gás ideal, de massas e , à mesma temperatura , sendo , tem a mesma energia cinética média, mas velocidades quadráticas médias diferentes.
4. De acordo com a interpretação estatística da Segunda Lei da Termodinâmica, certos processos são tão improváveis que na prática nunca acontecem.

As afirmativas CORRETAS são:

(a) Somente a IV.

(b) I, III e IV.

(c) Todas.

(d) Nenhuma.

(e) I, II e IV.

(f) III e IV.

A figura mostra o esboço de um diagrama para um gás ideal com um ciclo reversível formado por uma transformação a volume constante, uma transformação isotérmica e uma transformação adiabática, não necessariamente nesta ordem. O ciclo é percorrido no sentido .

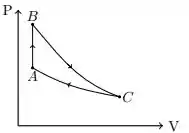
Considere as seguintes afirmações:

I. O calor é absorvido pelo gás na etapa e rejeitado na etapa .

II. O calor total transferido é negativo e o ciclo descreve um refrigerador.

III. A variação da entropia do gás a cada ciclo completo é nula.

IV. A variação da energia interna do gás, em módulo, é maior na etapa do que na etapa .

V. O calor é absorvido pelo gás na etapa e rejeitado na etapa .

As afirmativas corretas são:

(a) e .

(b) e .

(c) e .

(d) , e .

(e) , e .

1 - Uma máquina térmica opera entre as temperaturas de e . O fabricante da máquina afirma ser possível produzir de trabalho útil da mesma, retirando de calor do reservatório quente, e liberando de calor para o reservatório frio. A afirmação do fabricante pode ser verdadeira?

1. Sim, pois essa máquina obedece às leis da termodinâmica.
2. Não, pois essa máquina viola somente a primeira lei da termodinâmica.
3. Não, pois essa máquina viola somente a segunda lei da termodinâmica.
4. Não, pois essa máquina viola tanto a primeira quanto a segunda lei da termodinâmica.
5. É impossível dizer sem saber os processos envolvidos no ciclo termodinâmico da máquina.

Considere as seguintes afirmativas:

1. A variação da entropia de um sistema não depende da reversibilidade do processo termodinâmico mas a variação do conjunto sistema + vizinhança depende.
2. A variação da entropia de um sistema durante um processo reversível é oposta à variação da entropia da vizinhança. No entanto, durante um processo irreversível, um aumento da entropia do sistema é superior, em amplitude, à diminuição da entropia da vizinhança.
3. O desequilíbrio entre a variação da entropia de um sistema e de sua vizinhança durante um processo irreversível é devido a uma dissipação de energia que não pode mais ser usada para efetuar um trabalho. Não havendo dissipação durante um processo reversível, ele não resulta em um aumento da entropia do universo.

São verdadeiras:

1. Apenas I.
2. Apenas II.
3. Apenas III.
4. Apenas I e II.
5. Apenas II e III.
6. Apenas I e III.
7. Todas.
8. Nenhuma.

Como resultado de qualquer processo natural, a entropia total de todo o sistema mais a do seu ambiente:

1. Por vezes, diminui.
2. Nunca aumenta .
3. Sempre permanece a mesma.
4. Nunca diminui.
5. Impossível responder sem a informação da temperatura.

Uma maquina térmica:

1. Converte calor de entrada em uma quantidade equivalente de trabalho.
2. Converte trabalho em uma quantidade equivalente de calor.
3. Recebe calor, realiza trabalho, e perde calor.
4. Utiliza trabalho para transferir calor de um reservatório a baixa temperatura para outro reservatório a alta temperatura.
5. Em um ciclo produz trabalho equivalente ao calor rejeitado ao reservatório frio.

Do ponto de vista microscópico, é possível dizer que a 2a Lei da termodinamica surge do fato de que

A) Apesar dos movimentos microscópicos serem reversíveis, é mais provável que um sistema de muitas partículas interagentes evolua de um estado mais ordenado para um mais desordenado.

B) Apesar dos movimentos microscópicos serem irreversíveis, é mais provável que um sistema de muitas partículas interagentes evolua de um estado mais desordenado para um mais ordenado.

C) Apesar dos movimentos microscópicos serem reversíveis, é mais provável que um sistema de muitas partículas interagentes evolua de um estado mais desordenado para um mais ordenado.

D) Apesar dos movimentos microscópicos serem irreversíveis, é mais provável que um sistema de muitas partículas interagentes evolua de um estado mais ordenado para um mais desordenado.

E) Devido aos movimentos microscópicos serem reversíveis, é igualmente provável que um sistema de muitas partículas interagentes evolua de um estado mais desordenado para um mais ordenado, ou vice-versa.

Um gás ideal passa pelo processo reversível ilustrado na figura ao lado. Diga se as afirmações abaixo são verdadeiras [V] ou falsas [F]. Atenção, nesta questão cada resposta errada anula uma certa. Portanto, se não souber a resposta, é preferível não preencher a lacuna.

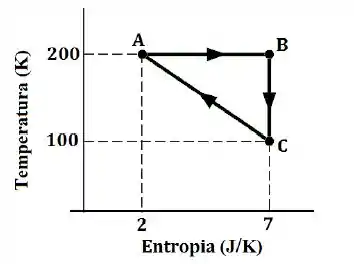
[ ] A variação de energia interna do gás após um ciclo foi de .

[ ] A velocidade média das partículas do gás no estado é o dobro da velocidade

média no estado C.

[ ] Não há troca de calor no processo .

[ ] No processo o gás perde de calor.

Marque a alternativa errada.

a) A entropia de um sistema pode variar mesmo se não houver troca de calor. Para isso, basta que ocorra um processo irreversível.

b) Um refrigerador é representado por um ciclo anti-horário no diagrama , ou seja, ele recebe trabalho e perde calor.

c) Se não houver troca de calor, a temperatura do sistema é constante.

d) de água em equilíbrio no estado sólido tem menos entropia que de água em equilíbrio no estado líquido.

e) A máquina de Carnot não consegue converter todo o calor recebido pela fonte quente em trabalho.

Um gás ideal sofre um processo reversível do seu estado inicial , ,  para o seu estado final , , . O gráfico mostra os dois caminhos possíveis, onde:

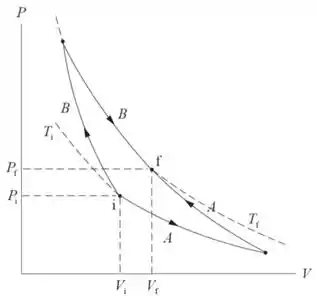
O gás sofre uma expansão isotérmica seguida de uma compressão adiabática.

O gás sofre uma compressão adiabática seguida de uma expansão isotérmica.

Sobre a variação de entropia  e a variação da energia interna  nos processos, é correto afirmar que

Nenhuma das alternativas anteriores.

Um determinado sistema tem variação de entropia negativa em determinado processo. O que se pode dizer COM CERTEZA sobre esse processo?

Escolha uma opção:

a. A variação da entropia do universo é zero.

b. O sistema está em contato com outro sistema, e a variação da entropia do universo deve ser

necessariamente positiva.

c. O sistema não está isolado. 

d. O processo é irreversível.

e. O processo é reversível.

.

Pretende-se submeter uma certa quantidade de um gás ideal aos seguintes processos:

I - Um processo adiabático reversível onde a energia interna do gás permaneça constante.

II - Uma diminuição de volume a pressão constante, onde a temperatura aumente.

III - Um processo onde todo o calor recebido pelo gás se converta em trabalho.

IV - Um processo onde todo o calor fornecido se converta em energia interna do gás.

Os seguintes processos são impossíveis, de acordo com as leis da termodinâmica:

(a) Somente I e II

(b) Somente I, II e III

(c) Somente II e III

(d) Somente I, II e IV

Uma barra de metal é conectada entre um reservatório quente e um reservatório frio. Devido a diferença entre os reservatórios, ocorre uma transferência de energia em forma de calor entre eles. Desprezando a variação de entropia da barra de metal, o que podemos dizer sobre o processo de variação de entropia do reservatório quente (), do reservatório frio () e do Universo ()?

(a) Irreversível,

(b) Reversível,

(c) Irreversível, ,

(d) Reversível,

(e) Irreversível

Num certo processo reversível, uma certa quantidade de um gás ideal é aquecida isotermicamente até que seu volume dobre. Num outro processo, este irreversível, a mesma quantidade de gás, partindo do mesmo estado de equilíbrio térmico inicial, sofre várias mudanças, mas atinge o mesmo estado de equilíbrio térmico final do caso reversível. Sejam as variações da energia interna e da entropia no processo reversível. Analogamente, sejam as variações da energia interna e da entropia no processo irreversível. Podemos afirmar que:

Caixas isoladas termicamente e divididas em duas partições possuem partículas distribuídas entre as duas partições, como mostrado nas figuras abaixo. Qual das configurações tem maior entropia?

Considere as seguintes afirmativas:

I. Toda a energia cinética de um objeto é transformada em calor;

II. Um refrigerador remove 100 J de calor dos alimentos em seu interior, usando apenas 75 J de energia elétrica;

III. Uma máquina térmica realiza 25 J de trabalho rejeitando apenas 10 J de calor para o reservatório frio;

Quais delas violam a 2a Lei da Termodinâmica?

(a) Apenas a afirmativa I viola a 2ª Lei.

(b) Apenas a afirmativa II viola a 2ª Lei.

(c) As afirmativas I e II violam a 2ª Lei.

(d) Todas as alternativas violam a 2ª Lei .

(e) Nenhuma das alternativas viola a 2ª Lei.

A respeito de processos REVERSÍVEIS sofridos por um gás ideal, podemos afirmar que:

(a) Para uma mesma variação positiva de volume a variação de pressão do gás é maior, em módulo, em um processo adiabático do que em um isotérmico.

(b) A entropia do gás sempre aumenta, para qualquer processo reversível.

(c) A variação da energia interna do gás é sempre igual à soma do calor PERDIDO pelo gás com o trabalho REALIZADO por ele.

(d) Para uma mesma variação de temperatura o calor fornecido AO gás a volume constante é igual ao calor fornecido a pressão constante.

(e) É possível realizar um ciclo em que o trabalho realizado pelo gás não seja nulo, mas que o calor total trocado entre o gás e o sistema seja nulo.

Considere dois reservatórios térmicos com temperaturas .

1. Os reservatórios são colocados em contato térmico durante um intervalo de tempo suficiente para que troquem de calor. Determine a variação de entropia do conjunto, , em .
2. Os mesmos reservatórios são utilizados para operar uma máquina de Carnot. Se de calor são absorvidos pelo reservatório frio em cada ciclo, qual a variação de entropia dos dois reservatórios, , em , ao final de um ciclo?

(Lembrete: Um reservatório térmico é, por definição, um sistema capaz de ceder ou absorver uma quantidade arbitrária de calor sem sofrer qualquer variação em sua temperatura).

Uma pá giratória está inserida em um recipiente selado e isolado termicamente, o qual contém um gás diatômico. A pá é acionada por uma corda conectada a um peso (fig.).

Quando o peso cai, fazendo a pá girar, verifica-se que a temperatura do gás aumenta.

Seria possível esta máquina funcionar ao reverso, ou seja: começando com o peso na altura do chão, seria possível que o gás reduzisse sua temperatura, ao mesmo tempo fazendo a pá rodar o contrário e erguer o peso?

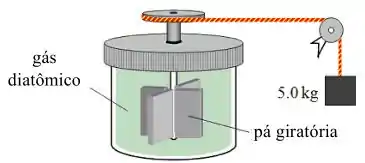
A) Sim, seria possível, pois este processo respeitaria todas as Leis da Termodinâmica

B) Não, devido à Lei Zero da Termodinâmica

C) Não, devido à 1a Lei da Termodinâmica apenas

D) Não, devido à 2a Lei da Termodinâmica apenas

E) Não, devido à 1a e 2a Leis da Termodinâmica

Qual das seguintes considerações está INCORRETA?

1. A segunda lei é uma lei empírica que mostra que certas coisas nunca acontecem. Portanto aceitamos em nosso formalismo que estas coisas são impossíveis.
2. A interpretação probabilística da segunda lei nos diz que certos eventos são tão improváveis que desprezamos a probabilidade de que eles aconteçam.
3. A entropia de qualquer sistema sempre aumenta com o tempo.
4. A partir de processos irreversíveis em sistemas isolados, determinamos o sentido da flecha do tempo.

A segunda Lei da Termodinâmica tem aplicação na natureza, é importante na obtenção de energia pelos seres vivos. A energia solar é absorvida pelos vegetais fotossintetizantes e realiza uma série de transformações, em cada um dos processos, a energia útil torna-se menor, dessa forma, os seres vivos não são capazes de sintetizar seu próprio alimento. O entendimento básico das leis da Física, leva-nos a buscar soluções para os problemas ambientais que o planeta tem vivenciado, como o efeito estufa, os furacões, terremotos, etc. A Segunda lei da Termodinâmica pode ser enunciada da seguinte forma:

a) é impossível ter um sistema que converta completamente e continuamente a energia térmica em outra forma de energia.

b) todos os sistemas são capazes de converter energia térmica em outra forma de energia, desde que a transformação seja isotérmica.

c) não existe calor nesse sistema porque a energia interna é nula.

d) a variação da energia interna de um sistema é sempre igual ao trabalho realizado pelo sistema.

e) a variação da energia interna de um sistema ocorre porque o calor flui de um corpo frio para outro quente

Um engenheiro propôs à sua empresa construir uma máquina térmica onde um gás ideal monoatômico sofre os processos indicados no diagrama da figura:

: processo isotérmico

: processo adiabático

: processo adiabático

A proposta foi rejeitada.

Quais das afirmativas abaixo são justificativas corretas para esta rejeição:

1. Esta máquina não funciona pois viola a segunda lei da termodinâmica.
2. Esta máquina não interessa pois tem uma eficiência muito baixa.
3. O ciclo é inconsistente. Uma das etapas indicadas não pode ocorrer.
4. Esta máquina não funciona pois viola a primeira lei da termodinâmica.

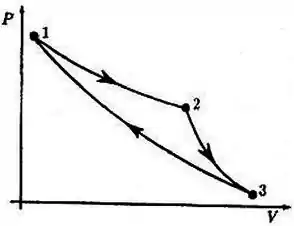
1. I e III
2. I e IV
3. I
4. IV
5. II e IV

Sobre máquinas térmicas podemos afirmar:

a) podem converter calor integralmente em trabalho

b) convertem calor parcialmente em trabalho, expelindo a outra parte para um reservatório frio

c) usam trabalho externo para extrair calor de um reservatório quente

d) possuem um rendimento máximo limitado pelo rendimento de uma máquina reversível

e) duas das outras respostas são verdadeiras

Em um dia úmido, o vapor d’água se condensa sobre uma superfície fria. Neste processo, a entropia DA ÁGUA:

1. Aumenta, pois o processo é irreversível.
2. Diminui.
3. Fica constante, pois não há variação de temperatura na mudança de fase.
4. Não é possível dizer sem dados sobre a superfície fria.
5. Vai a zero, pois a água não estará mais na forma de gás.

Uma máquina térmica opera entre dois reservatórios a e . Ela absorve de calor do reservatório de temperatura mais elevada e executa 100 J de trabalho durante um ciclo. A opção que mais se aproxima do valor da variação da entropia do universo para este processo é:

Escolha uma opção:

1. -2,8J/K
2. 2,8J/K
3. 0,5J/K
4. 1,1J/K
5. 3,5J/K

.

Uma garrafa térmica contém, inicialmente, uma massa de água a uma temperatura de . Então, um cubo de gelo de massa a é introduzido na garrafa térmica. Sabendo que no estado de equilíbrio do gelo foi derretido, faça o que é solicitado abaixo. Suas respostas podem ser deixadas em termos de frações simplificadas.

1. Determine a massa de água
2. Sem fazer contas, discuta quais devem ser os sinais esperados para as variações de entropia do gelo, da água e do sistema total (água + gelo). Ou seja, diga se cada uma dessas variações deve ser positiva, negativa ou nula. Explique suas respostas
3. Calcule a variação de entropia do gelo e da água

Dados:

Considere os processos: (i) Um objeto é lançado sobre uma mesa com coeficiente de atrito cinético e, devido à ação do atrito, atinge o repouso após certo intervalo de tempo; (ii) Um gás confinado a um recipiente em contato com um reservatório térmico expande isotermicamente. Qual da alternativas abaixo corresponde, respectivamente, à variação de entropia do sistema objeto+mesa no processo (i) e a variação da entropia do gás no processo (ii).

Marque a afirmação errada:

a) Para as mesmas fontes fria e quente, nenhuma máquina real pode ter uma eficiência maior que uma máquina de Carnot.

b) Em um sistema fechado, o estado de equilíbrio é o que possui maior entropia e maior número de microestados.

c) Se S é a entropia de um sistema fechado, ∆S > 0 para processos reversíveis e ∆S = 0 para processos irreversíveis.

d) A entropia de um sistema depende apenas do estado do sistema, e não do processo que o levou ao seu estado.

e) Nenhuma máquina térmica pode converter integralmente o calor recebido em trabalho.

f) A variação de entropia de um sistema que fornece calor pode ser negativa.

Em quatro experimentos, os blocos A e B, inicialmente a temperaturas diferentes, foram colocados juntos em uma caixa isolada até atingirem uma temperatura final comum. As variações da entropia dos blocos nos quatro experimentos possuem, não necessariamente na ordem dada, os valores a seguir (em J/K). Determine a que valor de A corresponde cada valor de B

Escolha uma:

1. 9 e -8, 8 e -3, 5 e -5, 3 e -2;
2. 9 e -3, 8 e -5, 5 e -2, 3 e -3;
3. 9 e -5, 8 e -8, 5 e -3, 3 e -2;
4. 9 e -2, 8 e -3, 5 e -3, 3 e -2;
5. 9 e -8, 8 e -5, 5 e -3, 3 e -2;

O volume de uma amostra de gás ideal é reduzido adiabaticamente de para . A pressão e a temperatura iniciais valem e , e a pressão final vale .

a) O gás é monoatômico, diatômico ou poliatômico?

b) Calcule a temperatura final do gás e dê a resposta em graus Celsius.

c) Calcule o número de mols da amostra.

d) Calcule o trabalho associado ao processo, e responda se o trabalho foi realizado sobre ou pelo gás.

e) Qual a variação da entropia ao final do processo.

Um bloco que desliza sobre uma superfície áspera desacelera e eventualmente para. O processo inverso nunca ocorre. Isto é, um bloco em repouso não começa a se mover e acelerar sobre uma superfície áspera sem a ação de um agente externo. A segunda situação é proibida porque violaria

1. A conservação da energia total
2. A conservação do momento
3. A primeira lei da termodinâmica
4. A segunda lei da termodinâmica
5. A primeira lei e a segunda lei da termodinâmica

Um recipiente isolado termicamente contém de gelo no ponto de fusão. Adiciona-se vapor de água a até que se obtenha água à temperatura de equilíbrio de .

1. Calcule a massa de vapor de água adicionado
2. Calcule a variação de entropia do sistema vapor-gelo-água nesse processo

Dados:

Um cubo de gelo a é colocado em uma banheira muito grande cheia com água a e derrete sem causar uma mudança apreciável na temperatura da água da banheira. Qual das seguintes afirmações é verdadeira?

A) A entropia ganha pelo cubo de gelo é igual a entropia perdida pela água.

B) A entropia perdida pelo cubo de gelo é igual a entropia ganha pela água.

C) A mudança total de entropia do sistema (cubo de gelo + água) é zero porque nenhum calor foi adicionado.

D) A entropia do sistema (cubo de gelo + água) aumenta porque o processo é irreversível.

E) A entropia da água não muda porque sua temperatura não mudou.

Um processo conhecido na metalurgia há muitos séculos é a têmpera do aço. Este processo que consiste no esfriamento rápido do aço aquecido a altas temperaturas serve para endurecer o metal, mas deve-se tomar o cuidado de fazer o processo nas temperaturas corretas, pois ao invés de se ter um metal endurecido, podemos ter no final um material frágil. Para fazer uma têmpera, um artesão aquece uma espada de de um aço até a temperatura de e em seguida a resfria rapidamente em um tanque com paredes adiabáticas contendo de água inicialmente a . Após a têmpera o sistema espada-água atinge o equilíbrio térmico na temperatura de .

de águade água

a) Determine o calor específico deste aço.

b) Qual a variação da entropia do sistema formado pela espada e a água no processo de resfriamento do aço? Este processo é reversível? O valor obtido está de acordo com a 2º lei da termodinâmica?

Parte II – Dois termômetros são colocados em um recipiente com água a uma temperatura X. Um termômetro está calibrado na escala Celsius e o segundo na escala Fahrenheit. Sabendo que o valor indicado na escala Celsius corresponde a metade do que indicado na escala Fahrenheit, determine qual o valor desta temperatura em Kelvin. (Ponto de fusão do gelo: ; ponto de ebulição da água ).

Calcule a variação de entropia associada ao processo de evaporação de de mercúrio, sabendo que o material evapora a .

(Dados: calor latente de evaporação = ; calor específico à temperatura ambiente ).