Encontre a aproximação para usando polinômio interpolador de Newton de grau usando os dados abaixo:
![]()
Passo 1
Vamos lááá! Para achar o polinômio interpolador de Newton, vamos precisar de um operador chamado de diferenças divididas que são os do polinômio interpolador :

Nosso primeiro passo então será construir a tabela de Diferenças Divididas que nos ajudará a encontrar os valores de , show de bola?!
Beleza... mas como montamos essa tabela mesmo? É assim ó,

Passo 2
Assim, substituindo os valores que temos do enunciado, ficamos com
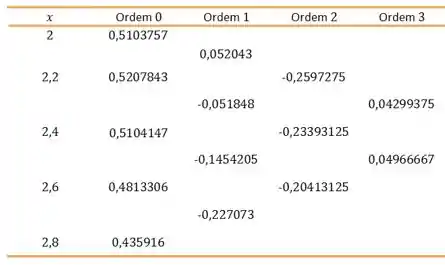
Beleza?!
Agora, um polinômio de grau requer valores . Como queremos uma aproximação em usamos:
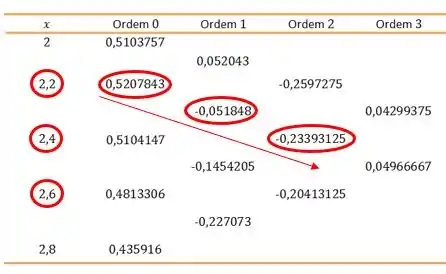
E temos:
Assim, nosso será:
Aproximando no nosso ponto de interesse: