Momento Fletor
Produzido por Pablo RicardoTeoria
O Momento Fletor nada mais é do que a soma dos momentos relativos a seção
Ele produz um esforço que tende a curvar a estrutura em relação ao seu eixo longitudinal, provocando tensões normais de tração e compressão na estrutura.
Que?! 😵💫😵💫😵💫
Imagina essa peça aqui:
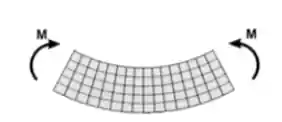
Percebe como a peça esta se curvando? É esse o efeito do momento fletor, ele é uma resultante de todos os momentos produzidos em uma estrutura e seu efeito é dobra-la.
É muito importante a gente se atentar ao sinal do momento fletor!
Vamos considerar o momento fletor positivo sempre que ele estiver tracionando a parte debaixo da viga e comprimindo a parte de cima. Desse jeito aqui:

Já um momento fletor negativo faz as fibras superiores tracionarem e as inferiores comprimirem, assim:
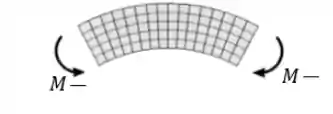
Beleza, mas agora vamos aprender a calcular o momento fletor e aplicar esse conceito nas nossas vidas?
Efeitos Internos de Uma Viga
Nosso primeiro passo é aprender a calcular os efeitos internos de uma viga!
Se liga nesse vídeo iradoso que o Responde Aí preparou especialmente pra você 👇
Maneiro, não é?!
Agora podemos voltar pra nossa saga do momento fletor!
Um artifício visual muito usado aqui em Estática é o diagrama de momento fletor, que é uma gráfico do valor do momento fletor ao longo de uma viga. Para uma análise mais completa também usamos o o diagrama de esforços cortantes.
Não se preocupa, vamos aprender tudinho sobre esses dois carinhas!
Diagramas de Momento Fletor e Esforços Cortantes
Agora que a gente já aprendeu a calcular os esforços internos de uma viga a gente pode representar isso graficamente, fazendo o diagrama de momento fletor (DMF) e o diagrama de esforço cortante.
Pra ficar tudo bem claro, vamos fazer o diagrama de momento fletor (DMF) e o diagrama de esforço cortante pra seguinte viga:
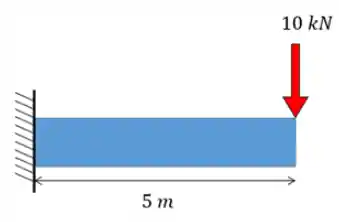
Passo 1: Calcular as Reações de Apoio
Antes de qualquer coisa a gente vai esquematizar as reações:
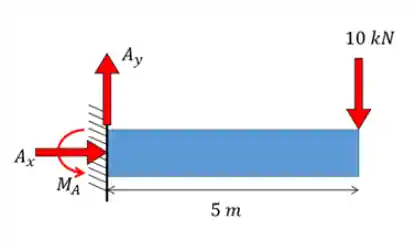
Como estamos em equilíbrio, podemos dizer que o somatório de força e de momento são iguais a zero:
Para o eixo horizontal temos:
Para o eixo vertical:
Para o momento aplicado em
Passo 2: Calcular as Reações Internas
Agora podemos fazer uma seção para calcular a força cisalhante, normal e momento fletor:
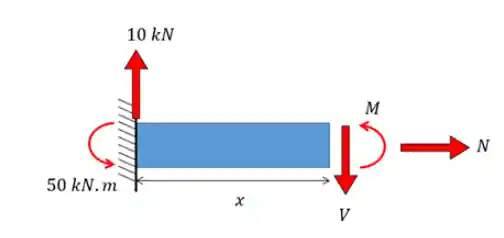
Trazendo novamente as equações da estática, primeiro para o eixo horizontal:
Agora para o eixo horizontal:
Logo a cortante é constante e igual a 10.
Para o momento, aplicado em
Essa é a nossa equação do diagrama do momento fletor!
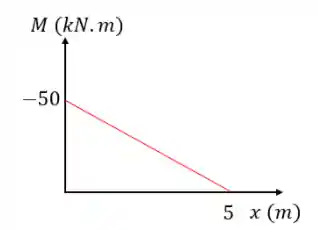
Passo 3: Plotar o Diagrama de Momento Fletor (DMF)
O diagrama de momento fletor (DMF) nada mais é que um gráfico que relaciona o comprimento de uma viga e o valor do momento fletor. Na prática você coloca o comprimento da viga no eixo
Para o nosso exemplo o momento fletor tem a seguinte equação:
Para fazer o diagrama de momento fletor a gente calcula em que posição o momento fletor é igual a zero
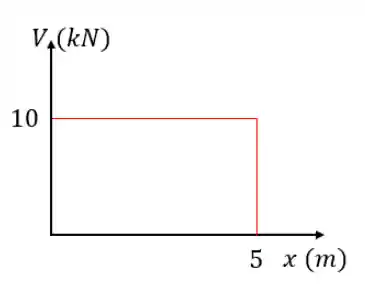
Passo 4: Plotar o Diagrama de Esforço Cortante
O diagrama de esforço cortante (DEC) também é um gráfico onde você coloca o comprimento da viga no eixo
Vimos que a força cortante é uma constante, igual a
Se a força cortante é uma constante, o diagrama de esforço cortante vai ser uma reta, assim:
Agora vamos praticar com exercícios?