Vigas – Efeitos Internos
Produzido por Pablo RicardoTeoria
Introdução
Dê uma olhada na viga abaixo:

Se eu aumentar a força continuamente, essa viga irá se quebrar? O que leva ao rompimento da viga?
Para responder esta pergunta, temos que estudar o que acontece internamente na viga quando aplicamos uma carga. Chamamos as forças e momentos que surgem dentro da viga de esforços ou efeitos internos.
Para entender os esforços internos, vamos pegar a viga acima, cortar ao meio e ver o que acontece na seção .
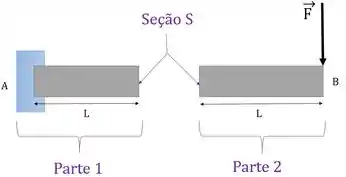
Sempre que cortamos uma viga como fizemos nesse caso acima, temos que levar para a seção correspondente a contribuição que uma das partes faz na outra. Ou seja, temos que levar para a seção da parte 1 todas as forças da parte 2 e seus respectivos momentos:
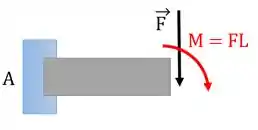
O que fizemos neste caso foi levar a força até a seção e o momento que ela faz em relação a esse ponto em que cortamos a viga.
Sabendo disso, agora vamos saber quais são os esforços internos:
Força cisalhante ou cortante
Vamos chamar essa força de e ela é sempre paralela à seção , ou seja, vai aparecer sempre que existirem forças transversais, perpendiculares, à peça, assim:
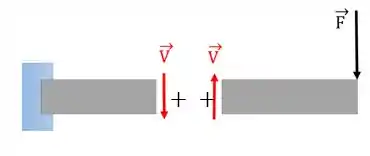
Repare que o caso a cima traz dois exemplos nas quais o cortante é positivo. Analogamente podemos defindir também os cortantes negativos:
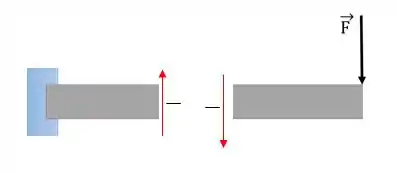
Lembre-se bem dessas notações de sentido, elas são bem importantes!
Além disso, que o cortante vai ser igual à resultante de todas as forças que você leva de uma das partes até a seção . Nesse caso do exemplo, o cortante vai ser igual à força .

Se você prefirir, ao invés de ficar levando as forças com seus momentos de um lado para o outro, pode fazer o equilíbrio de uma das partes como estamos acostumados. Você coloca o cortante na seção e utiliza para achar o seu valor, assim:

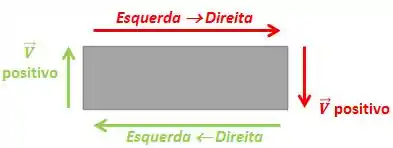
ATENÇÃO! ![]() Vamos adotar o seguinte critério: Se estivermos indo da esquerda para a direita, o cortante positivo será com a seta para baixo...e quando estivermos indo da direita para esquerda, o cortante será positivo quando a seta estiver apontando para cima.
Vamos adotar o seguinte critério: Se estivermos indo da esquerda para a direita, o cortante positivo será com a seta para baixo...e quando estivermos indo da direita para esquerda, o cortante será positivo quando a seta estiver apontando para cima.
Normal
A normal vai aparecer sempre que tivermos uma força axial (na direção do eixo da peça). Vamos chamar esta força de e ela sempre é perpendicular à seção .

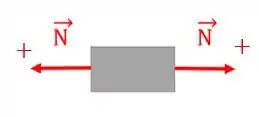
A normal será positiva quando estiver com a setinha apontando para fora da viga e quando isso acontecer dizemos que a força está tracionando a estrutura. Ou seja, quando a peça estiver sendo tracionada (esticada) a normal é positiva!
E a normal será negativa quando estiver com a setinha apontando para dentro da viga e quando isso acontecer dizemos que a força está comprimindo a estrutura.
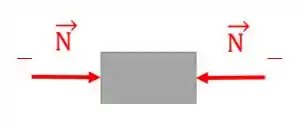
Perceba que os esforços internos sempre ocorrem em pares iguais e de sentidos contrários.
Momento fletor
Momento Fletor é justamente a resultante de todos os momentos produzidos quando levamos as forças de uma parte até a seção .
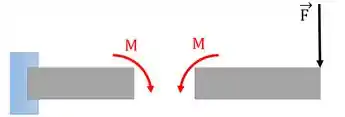
O efeito do momento fletor é dobrar a estrutura assim:
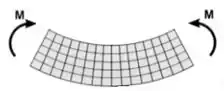
E quando o momento fletor é positivo? Vamos considerar positivo sempre que ele estiver tracionando a parte debaixo da viga e comprimindo a parte de cima. Desse jeito aqui:


Cuidado: para ver se o momento fletor é positivo não usamos a regra da mão direita.
Já um momento fletor negativo faz as fibras superiores tracionarem e as inferiores comprimirem:
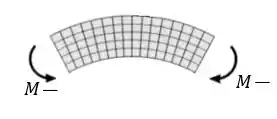
Exemplo
Vamos ver um exemplo para ficar mais claro. Queremos calcular os esforços internos na seção da viga abaixo:

Passo 1: Calcular as reações de apoio. Para isso vamos utilizar as equações da estática:
Começando pelo eixo horizontal:
Para o eixo vertical:
E finalmente para o momento, aplicado em e com direção anti-horária positiva
Repare que, ao aplicar o momento em , temos apenas dois termos: o do próprio engaste e da força de .
Assim vamos ter:

Passo 2: Separar a viga na seção .
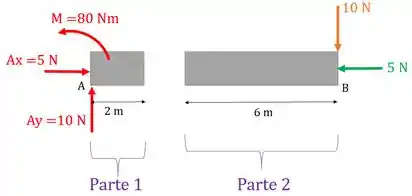
Passo 3: Escolher uma das partes e levar a contribuição da outra parte para a sua respectiva seção. Nessa etapa, é mais fácil escolher a parte com maior quantidade de forças e momentos. Então, vou escolher a parte 1 e levar todas as forças de e da parte 2 com os seus respectivos momentos para a seção da parte 1.
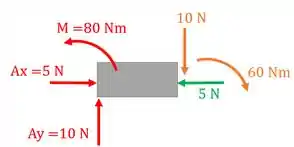
Repare que a força de não tem momento com relação à seção , pois estamos desprezando a altura da viga.
Uma coisa importante e que ajuda a verificar se está tudo certinho é que cada parte tem que estar em equilíbrio.
Passo 4: Olhar para a seção e verificar o que é o quê.
- Cortante: A força de é paralela à seção , então ela corresponde ao cortante. Agora vamos comparar com aquele esqueminha para saber se é positivo ou negativo:
- Momento Fletor: o momento que está na seção é o nosso momento fletor. Repare que a setinha empurra a parte de baixo da viga e puxa a sua parte de cima. Ele está contrário ao sentido que estabelecemos como positivo.
- Normal: a força que está perpendicular à seção será a nossa normal. E para sabermos se ela é positiva ou negativa temos que comparar com o nosso esqueminha.
- Se você tiver a equação do cortante é só derivar e multiplicar por para saber a equação do carregamento:
- Se você tem a equação do momento fletor é só derivar para achar a equação do cortante:
- Caso você tenha uma equação do momento fletor é só derivar duas vezes para obter a equação do carregamento e multiplicar por :
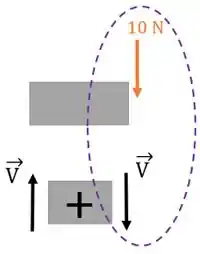
Repare que a força de está com a setinha apontando para o mesmo sentido que o cortante positivo do nosso esquema. Então, o cortante na seção é:
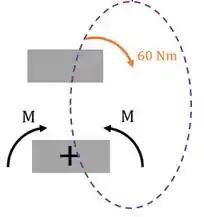
Então, nosso momento fletor será:
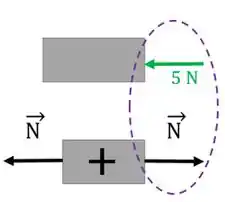
Repare que a força de está apontando para dentro da viga e está com sentido contrário ao que estabelecemos como positivo. Então, a normal na seção é:
Relações Diferenciais
Bom, existem certas relações diferenciais entre o momento fletor, o cortante e a carga distribuída:
Se tivermos a seguinte equação do carregamento: . Repare que essa é uma equação do primeiro grau. Então, a equação do cortante será do segundo grau e a do momento fletor será de terceiro grau. Saber isso será muito útil para verificar se não cometemos nenhum erro no meio do caminho.
Use e abuse dessas relações.
Força cisalhante ou cortante
Normal
Momento fletor
Exemplo
Relações Diferenciais
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2012, 213, 5/117
Determine as distribuições da força cortante e do momento fletor produzidos na viga pela carga concentrada. Quais são os valores do cortante e do momento em ?
Passo 1
Vamos calcular primeiro as reações de apoio no ponto
Pelo equilíbrio de forças verticais, temos que:
Agora vamos fazer o somatório de momentos com relação ao ponto e considerar o momento positivo girando no sentido anti-horário:
Pronto, agora já sabemos as reações de apoio.
Passo 2
Vamos agora calcular o cortante e o momento fletor. Para isso, vamos analisar o que acontece quando fazemos um corte na viga um pouco infinitésimo antes de onde está a carga :
Repare que cortamos a viga em , mas sem pegar a carga !!!
Note também que surge um momento e um cortante na parte da viga que cortamos. Para achar o valor de podemos fazer o equilíbrio das forças verticais:
No ponto da viga temos um cortante que é devido à reação de apoio. Vamos analisar o sinal dos cortantes que temos:
Repare que eles são positivos, pois as setas estão no mesmo sentido do cortante que estabelecemos como positivo.
Agora vamos ver o momento fletor...
Considerando o momento positivo girando no sentido anti-horário, vamos fazer o somatório de momentos com relação ao ponto onde cortamos a viga, ou seja, em :
Então, o momento fletor na seção que cortamos a viga é zero.
Mas no início da viga, ou seja, no ponto existe um momento fletor que é a nossa reação de apoio devido ao engaste. Vamos analisar o seu sinal:
Repare que o nosso momento gira no sentido contrário do momento fletor que estabelecemos como positivo, então ele é negativo:
Passo 3
Agora vamos cortar a viga um infinitésimo depois do ponto onde está a carga :
Repare que cortamos a viga em , mas incluindo a carga !!!
Note também que surge um momento e um cortante na parte da viga que cortamos. Para achar o valor de podemos fazer o equilíbrio das forças verticais:
Ou seja, o cortante é zero um infinitésimo depois da carga . Isso ocorre porque toda vez que tivermos uma carga concentrada teremos descontinuidade do cortante.
O momento fletor nesta seção vai ser zero também, como já fizemos antes.
Passo 4
Agora vamos fazer analisar o que teremos no final da viga:
Aqui cortamos a viga em .
Note também que surge um momento e um cortante na parte da viga que cortamos. Para achar o valor de podemos fazer o equilíbrio das forças verticais:
Ou seja, o cortante continua sendo zero nesta parte da viga!
Considerando o momento positivo girando no sentido anti-horário, vamos fazer o somatório de momentos com relação ao ponto onde cortamos a viga, ou seja, em
Então, o momento fletor no final da viga também é zero.
Passo 5
Agora temos que montar os nossos diagramas. O diagrama de cortante fica assim:
Repare que no ponto onde a carga concentrada está existe uma descontinuidade do cortante!
E o diagrama de momento fletor fica assim:
É só marcarmos os valores que achamos em cada seção que fizemos na viga e ligar os valores.
Passo 6
Agora precisamos saber quanto vale o cortante e o momento fletor em .
Observando nosso diagrama, em vamos ter que:
Ou seja, o cortante é:
Para saber o momento fletor vamos fazer um corte na viga em :
Agora é só fazermos o somatório de momentos com relação à :
Agora vamos analisar o seu sinal:
Como o momento fletor que achamos gira no sentido contrário ao que consideramos como positivo, então ele é negativo:
Resposta
Exercício Resolvido #2
R. C. Hibbeler, Estática mecânica para engenharia, 10ª ed. São Paulo: Pearson Prentice Hall, 2005, pp.286 – Ex 7.3.
As forças atuam no eixo mostrado, Determina a força normal interna nos pontos e .
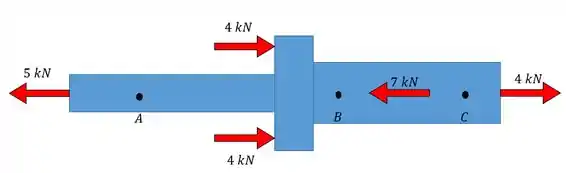
Passo 1
E aí, meus queridos e minhas queridas!! Olha só esse problema, perceba que ele já forneceu todas as forças externas atuantes e pede apenas a força normal interna.
Como vamos resolver isso? Bom, se o problema já nos forneceu todas as forças externas então basta fazermos as seções nos pontos dados e calcular a força axial interna:
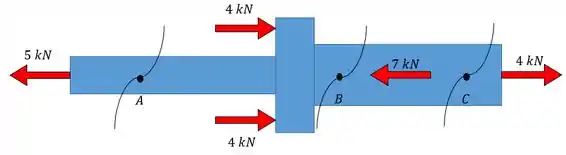
Passo 2
Vamos começar pela seção em :
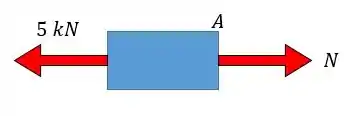
Pessoal, reparem que o problema não pediu nem a cortante nem o momento fletor então não precisamos nos preocupar com esses valores ok!? Só com a normal mesmo, e lembra que a normal é sempre axial ao eixo.
Trazendo a equação da estática para o eixo vamos ter:
Como é positivo então temos uma força de tração, que estica a peça!
Passo 3
Vamos começar pela seção em :
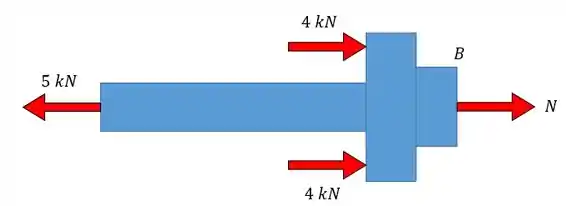
Trazendo a equação da estática para o eixo vamos ter:
Como é negativa então temos uma força de compressão!
Passo 4
Vamos começar pela seção em , dessa vez eu vou fazer o corte pela esquerda (que vai facilitar os cálculos). Reparem que o importante é sempre deixar a força normal para fora da peça!!
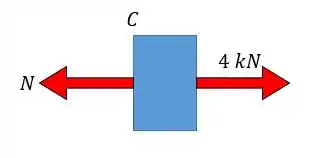
Trazendo a equação da estática para o eixo vamos ter:
Como é positiva então temos uma força de tração!
Se fizéssemos pelo outro lado então daria o mesmo resultado beleza?
Resposta
Para :
Pra :
Para :
Exercício Resolvido #3
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 213-5/118
Determine o cortante na seção , localizada entre e e o momento fletor no apoio .
Passo 1
Nosso primeiro passo neste tipo de questão é achar as reações de apoio e para isso temos que montar o diagrama de corpo livre:
Vamos começar nosso equilíbrio calculando o momento com relação ao ponto , pois neste ponto temos a maior quantidade de forças que são incógnitas:
Agora vamos fazer o somatório de forças em cada eixo. Perceba que no eixo só temos a força , logo ela será nula.
Passo 2
Nosso próximo passo é separar a viga na seção para calcularmos o cortante:
Vamos escolher uma das partes para fazer o equilíbrio! A dica aqui é escolher a parte da viga que tem a maior quantidade de forças, no nosso caso é a parte esquerda da viga:
Mas por que isso? Porque temos que levar todas as forças do pedaço que vamos descartar para a seção da parte que escolhemos. Desse jeito aqui:
Repare que a força da parte da viga que descartamos foi levada para a seção da parte da viga que escolhemos para fazer o equilíbrio. O nosso cortante vai ser justamente a força que está na seção .
Mas como fazemos para saber se esse cortante é positivo ou negativo? É só comparar com aquele esqueminha do cortante positivo que fizemos, assim:
Repare que a força aponta no mesmo sentido que o cortante positivo quando olhamos pela direita. Então, o cortante na seção é:
Passo 3
Agora temos que calcular o momento fletor no apoio . Então, vamos ter que cortar a viga nesse ponto, assim:
Qual parte vamos escolher para fazer o equilíbrio? Aquela que tem a maior quantidade de forças!
Temos que levar para a seção desta parte que escolhemos o momento que a força do outro pedaço faz com relação à seção .
Repare que para saber o sentido do momento (para onde a setinha aponta) usamos a regra da mão direita. Então, vamos calcular o valor desse momento :
Mas como fazemos para saber se esse momento fletor é positivo ou negativo? Ele é positivo quando está tracionando a parte de baixo da viga. Mas o nosso momento traciona a parte de cima da viga, logo ele é negativo.
Se está difícil de visualizar assim, você pode comparar com o nosso esqueminha de momento fletor positivo e ver se as setinhas estão iguais ou invertidas:
Perceba que as setinhas estão invertidas, então o momento fletor no apoio é:
Resposta
Exercício Resolvido #4
R. C. Hibbeler, Estática mecânica para engenharia, 10ª ed. São Paulo: Pearson Prentice Hall, 2005, pp.286 – Ex 7.7.
Determine a força de cisalhamento e o momento nos pontos e .
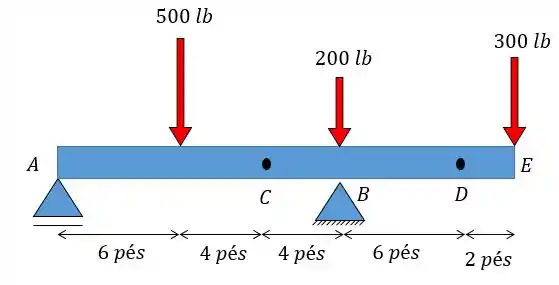
Passo 1
Fala aí, galera!!! Para determinarmos a força de cisalhamento e o momento fletor nos pontos e a gente tem que primeiro achar as resultantes em e em . Depois vamos fazer duas seções, onde? Exatamente nos pontos que estamos analisando e .
Nessas duas seções vamos aplicar as equações da estática e assim achar os esforços pedidos!
Passo 2
Show de bola! Vamos começar então analisando os apoios e . é um rolete, um apoio de 1° gênero, enquanto é um pino, um apoio de 2° gênero. Dessa forma as reações nesses apoios são dadas como:
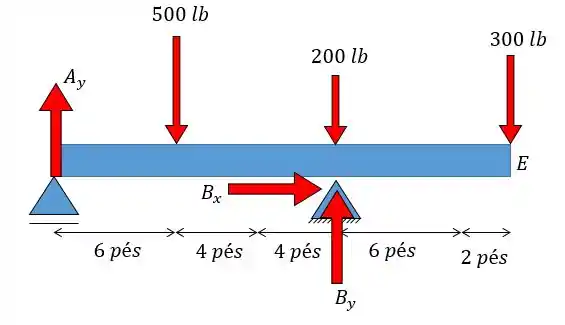
Uhulll!!! Agora é só aplicar as equações da estática:
Para as forças em vamos ter:
Para as forças em :
E finalmente para o momento, aplicado ao ponto e com sentido anti-horário positivo:
Substituindo na equação em vamos ter:
Prontinho! Temos as nossas reações.
Passo 3
Com essas reações vamos fazer um desenho do problema:
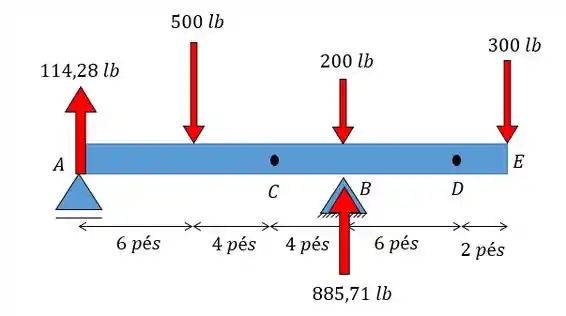
Show! Perceba que eliminamos as incógnitas referentes aos apoios! Agora é só fazermos as seções nos pontos que queremos. Vamos começar pelo ponto :
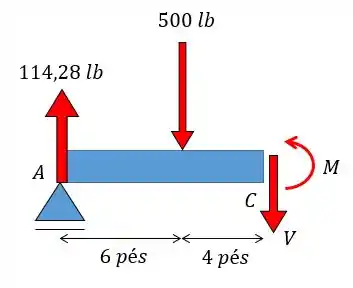
Como não existem esforços horizontais nesse problema eu nem me preocupei em colocar o efeito da normal, já que é nulo, beleza?
Continuando, agora é só fazermos a análise estática.
Para vamos ter:
Agora para o momento, aplicado em e com sentido anti-horário positivo:
Substituindo o valor da força cortante achada anteriormente:
Pronto! Para o ponto já está calculado!
Passo 4
Agora vamos fazer a mesma coisa para o ponto :
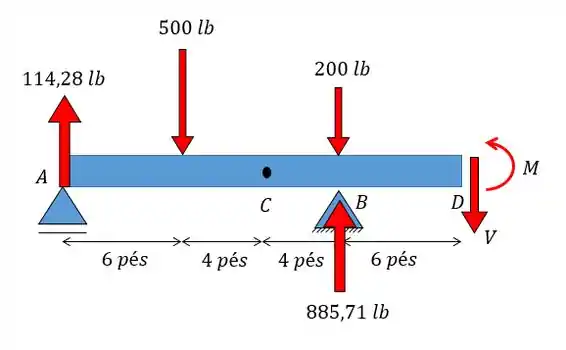
Vamos fazer a análise estática. Para vamos ter:
obs: A gente poderia ter feito pelo outro lado que iria dar menos trabalho! Veja como a cortante é igual à força que “sobrou”. Mas fiz por aqui pra te mostrar como que dá certinho!
Agora para o momento, aplicado em e com sentido anti-horário positivo:
Substituindo o valor da força cortante achada anteriormente:
Novamente poderíamos ter feito pelo outro lado e achado o mesmo valor! Mas é legal fazer pelo menos uma vez assim para ver que é verdade =D
Resposta
Para :
Para :
Exercício Resolvido #5
J.L. Meriam e L.G. Kraige,Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 213-5/121
Desenhe os diagramas de cortante e momento para a viga submetida a um momento em sua extremidade. Qual é o valor do momento em uma seção à direita de ?
Passo 1
Vamos começar achando as reações de apoio e para isso temos que fazer nosso diagrama de corpo livre:
Primeiro vamos calcular o momento com relação ao ponto .
Agora vamos fazer o somatório de forças em cada eixo.
Passo 2
Não esqueça que quando tem uma força concentrada em um ponto, haverá uma descontinuidade do cortante. E quando há um momento concentrado tem descontinuidade do momento.
Então, neste nosso exercício temos que calcular o cortante e o momento fletor nos pontos ,e .
Como teremos dois valores de cortante para um mesmo ponto? Ao fazer uma seção em um ponto onde tem uma força concentrada, não podemos dividir essa força ao meio.
Então, temos que fazer uma seção um tantinho antes ou um tantinho depois do ponto onde está a força. Mas é um tantinho mesmo, um infinitésimo, uma distância desprezível.
Olha o ponto A como fica quando fazemos a seção um infinitésimo antes da reação :
Ao escolher a parte , temos que levar todas as forças da parte com seus respectivos momentos até a seção da parte :
O cortante resultante nessa seção será zero e o momento fletor também será zero.
Dizemos que o cortante pela esquerda é zero e o momento fletor, que não tem descontinuidade, também é nulo, logo:
Mas e se escolhermos a parte ? Temos que levar as forças e momentos da parte para a seção da parte . Mas não tem nada na parte para ser levado, certo? Então a parte fica:
Neste caso, o valor do nosso cortante no ponto é de !!!
Percebeu o porquê da descontinuidade? Cada parte que escolho para equilibrar vai dar um valor de cortante diferente. Repare que o momento fletor no ponto dessa parte também é zero. Ele não muda, porque não tem nenhum momento concentrado neste ponto.
Agora temos que analisar o seu sinal e para isso vamos comparar com o nosso esqueminha de cortante positivo:
A reação está apontando para baixo enquanto que a setinha do cortante positivo aponta para cima, ou seja, o nosso cortante no ponto é negativo. Dizemos que o cortante pela direita é:
Passo 3
Vamos para o ponto agora. Neste ponto temos o mesmo problema: uma força concentrada.
Vamos fazer o mesmo procedimento: fazer a seção um tantinho à direita do ponto , assim:
Repare que a parte ficou com a força que está no ponto e a parte ficou sem essa força. Vamos fazer o equilíbrio da parte primeiro levando a contribuição da parte :
Então, o cortante na seção do ponto pela esquerda é:
E o momento fletor? Seu valor vai ser . Para sabermos o sinal, vamos comparar com o nosso esqueminha de momento positivo:
Portanto, nosso momento fletor vai ser:
Agora vamos fazer a mesma coisa para a parte . Antes de tudo vamos equilibrar esta parte levando a contribuição da parte :
Agora vamos achar a resultante das forças e momentos:
Perceba que o cortante agora é zero e que o momento fletor continuou o mesmo (já que não tem momento concentrado). Então, pela direita temos:
Passo 4
Agora vamos para o nosso último ponto, onde está o momento. Como não há nenhuma força neste ponto, não vai ter descontinuidade do cortante. Mas tem um momento concentrado aí, logo teremos uma descontinuidade do momento.
Vamos fazer uma seção um pouquinho à direita do momento de , assim:
Temos que equilibrar e achar a resultante na seção de cada uma das partes.
A parte já está equilibrada e não tem nada da parte para levar para esta seção:
Então, pela esquerda:
Fazendo a mesma coisa para a parte :
Então, pela direita:
Passo 5
Nosso último passo é fazer cada diagrama que nada mais é do que um gráfico de como os esforços internos variam ao longo da viga.
Vamos marcar no gráfico os pontos chaves que achamos.
- Cortante: perceba que só temos forças concentradas, então o cortante entre o trecho é constante:
- Momento Fletor: o cortante é a derivada do momento, então se temos o cortante e queremos saber o momento temos que integrar, certo? Portanto, o que é uma reta constante vai virar uma reta que varia linearmente.
Não esqueça que a integral de zero é uma constante!!!
Agora podemos responder qual é o valor do momento em uma seção à direita de só olhando nosso diagrama de momento fletor:
Resposta
Exercício Resolvido #6
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 213-5/125
Determine o cortante e o momento em uma seção da viga carregada à direita de .
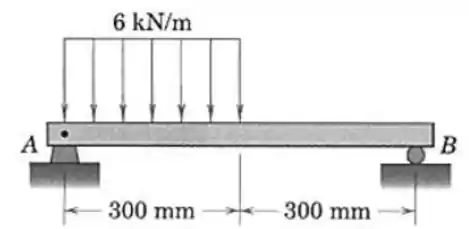
Passo 1
Primeiro temos que achar as reações de apoio e para isso temos que montar o diagrama de corpo livre:
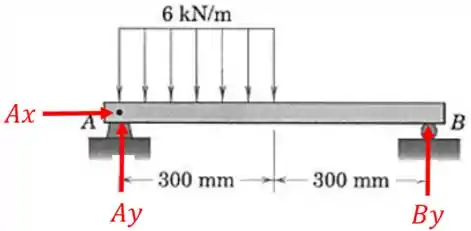
Vamos transformar a carga distribuída em uma única força resultante:
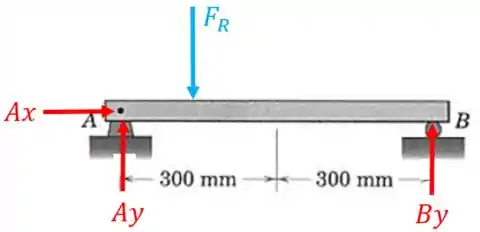
Como a carga distribuída é retangular, a força resultante será:
A localização da força resultante é na metade do comprimento do retângulo:
Então, vamos ter o seguinte diagrama de corpo livre:
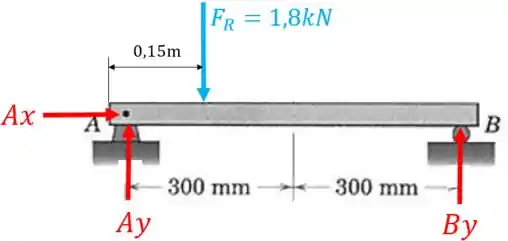
Agora podemos começar o equilíbrio calculando o momento com relação ao ponto , pois neste ponto temos a maior quantidade de forças:
Agora vamos fazer o somatório de forças em cada eixo.
Passo 2
Nosso próximo passo é separar a viga em uma seção à à direita do ponto .
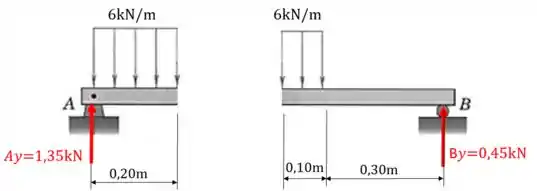
Agora tanto faz a parte da viga que escolhermos para fazer o equilíbrio. Mas vamos ficar com a parte da esquerda.
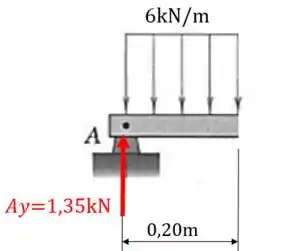
O próximo passo é levarmos tudo que está na parte direita para a seção da parte esquerda. Não esqueça que temos que levar a força e o momento que ela faz na seção! ![]()
Para facilitar, vamos calcular a resultante daquele pedacinho de carga distribuída que tem na parte direita.
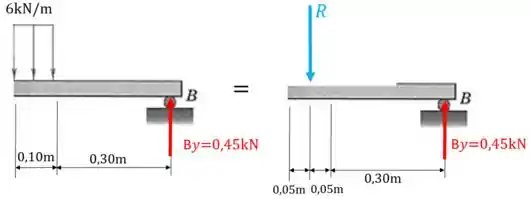
Agora vamos levar as forças e para a seção da parte esquerda com seus respectivos momentos, assim:
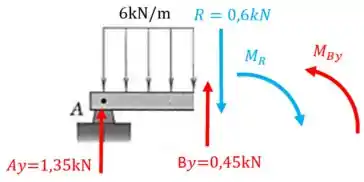
Não esqueça que o sentido da setinha do momento achamos pela regra da mão direita. Vamos calcular esses momentos:
Então, o que temos até agora é:
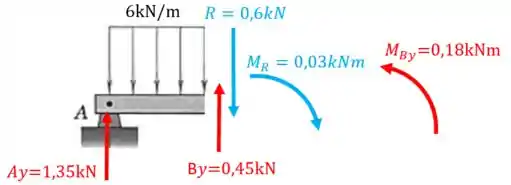
Agora temos que calcular as resultantes das forças e dos momentos nesta seção, assim:
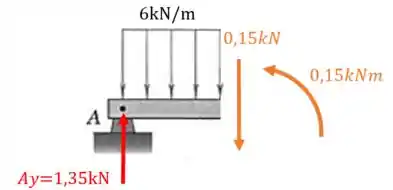
Passo 3
Afinal, qual será o nosso cortante? Será a força resultante naquela seção, ou seja:
Mas ele será positivo ou negativo? É só compararmos com o nosso esqueminha de cortante positivo:
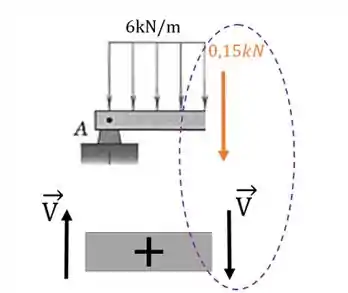
Repare que o nosso cortante aponta para baixo, o mesmo sentido do cortante positivo quando olhamos pela direita, então:
Passo 4
E o momento fletor? Ele será o momento resultante naquela seção, ou seja:
Para sabermos o sinal do momento fletor é só comparar o nosso momento com o esqueminha do momento fletor positivo:
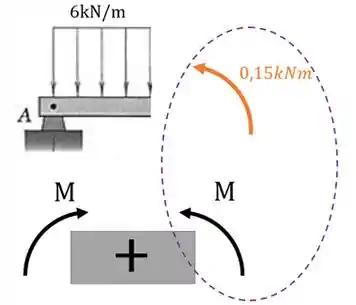
O nosso momento de está apontando para o mesmo sentido do momento positivo, então, o momento fletor nesta seção é:
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2012, 240, 5/215
Determine o momento fletor máximo, , para a viga carregada e especifique a distância à direita da extremidade onde ocorre.
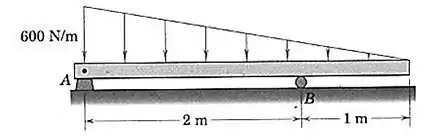
Passo 1
O primeiro passo é definir uma equação para a força distribuída. Observe que essa distribuição tem o formato de uma reta inclinada, então podemos escrever:
O valor de pode ser encontrado através pela tangente do triângulo:
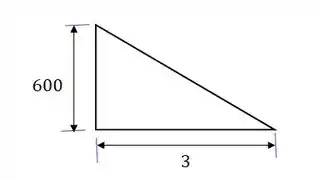
Como a reta está decrescendo, o valor de será negativo!
Assim, a nossa equação do carregamento fica:
E quando temos que , então substituindo isso na nossa equação vamos ter que:
Então, a nossa equação do carregamento distribuído ficou:
Passo 2
Vamos calcular a força resultante da carga distribuída e para isso é só calcularmos a área do triângulo:
E a sua posição em relação ao ponto
Vai ser dada por da altura do triângulo:
Além disso, precisamos calcular as reações em e também. Primeiro vamos fazer o somatório de momentos com relação ao ponto e considerar como positivo o momento no sentido anti-horário:
E agora vamos fazer o somatório de forças verticais:
Passo 3
Sabemos que para achar a equação do cortante precisamos integrar a equação do carregamento e multiplicar o resultado por :
Mas temos que fazer isso para cada intervalo da viga. O primeiro vai de a :
Esse é a constante de integração. Mas qual será o seu valor?
Sabemos que quando , o valor do cortante será igual ao valor da reação:
Então, vamos substituir isso na nossa equação:
Então, a equação do cortante para o trecho da viga que vai de até é:
Portanto, quando , o nosso cortante será:
Passo 4
Agora vamos fazer o mesmo para o outro trecho da viga, ou seja, vamos integrar a equação do carregamento:
Mas repare que a constante de integração mudou para . Mas por que fizemos isso?
Porque no ponto vai ter uma descontinuidade do cortante já que existe a reação neste ponto:
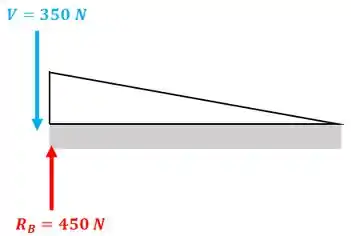
Não esqueça que o cortante é negativo, por isso está apontando para baixo!
Então, nesse novo trecho da viga quando vamos ter que o cortante resultante será:
Vamos substituir isso na nossa equação:
Então, a equação do cortante para o segundo trecho da viga que vai de até é:
Passo 5
Nosso próximo passo é achar a equação para o momento fletor!
Para isso temos que integrar cada equação do cortante que achamos:
Então, para o primeiro trecho da viga vamos ter que:
Sabemos que na extremidade , o momento fletor deve ser zero, então:
Então, a nossa equação fica:
Passo 6
E para o segundo trecho da viga vamos integrar a nossa outra equação do cortante:
Agora sabemos que quando , o momento fletor será zero:
Então, a nossa equação fica:
Passo 7
Para saber onde ocorre o momento máximo é só derivarmos a equação do momento e igualar a zero:
Mas qual das duas equações de momento que achamos?
Repare que na primeira região da viga é que teremos o maior momento, pois tem o maior valor de carregamento, então vamos derivar a primeira equação:
Resolvendo esta equação do segundo grau vamos obter duas raízes:
Como o primeiro resultado é maior que o comprimento da viga, devemos descartá-lo!
Então, o momento máximo ocorre quando
E qual será o seu valor? É só substituirmos esse valor de na nossa equação do momento :
Resposta
Exercício Resolvido #8
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 214, 5/126
Determine o cortante e o momento em uma seção à direita da extremidade da viga.
Passo 1
O primeiro passo é definir uma equação para a distribuição de forças. Observe que essa distribuição tem o formato de uma reta, então podemos escrever:
O valor de pode ser encontrado através pela tangente do triângulo:
Assim:
Passo 2
Vamos calcular a força resultante da carga distribuída:
E a sua posição em relação ao ponto
Vai ser dada por da altura do triângulo:
Além disso, precisamos calcular as reações em e também. Primeiro vamos fazer o somatório de momentos com relação ao ponto e considerar como positivo o momento no sentido anti-horário:
E agora vamos fazer o somatório de forças verticais:
Passo 3
A representação do nosso sistema é essa aqui:
Repare que quando cortamos a viga em uma posição qualquer surge o cortante e o momento fletor na seção.
A força resulta em qualquer posição da viga pode ser calculada assim:
Então essa é a nossa equação para calcular a força resultante devido ao carregamento distribuído em qualquer posição da viga!
E o momento com relação ao ponto causado por esta força resultante é:
Então, para vamos ter que a força resultante será de:
E o seu momento com relação ao ponto será:
Passo 4
Para achar e, basta a gente fazer o equilíbrio da viga usando as condições:
Então, vamos quando teremos o seguinte:
Vamos fazer o somatório de forças:
Esse cortante é positivo ou negativo? Para descobrir isso temos que comparar com o nosso esqueminha de cortante positivo:
Repare que o cortante que encontramos aponta no mesmo sentido do cortante que convencionamos como positivo, então ele é positivo:
E agora vamos fazer o somatório de momentos com relação ao ponto considerando o momento positivo girando no sentido anti-horário:
Esse é o momento da força resultante () com relação ao ponto e que nós já calculamos no passo anterior:
Então, vamos ter que:
Repare que o nosso momento deu negativo, isso significa que arbitramos um sentido contrário para ele. Na verdade ele é assim:
Mas esse momento fletor é positivo ou negativo segundo a nossa convenção? Para responder isso vamos comparar com o nosso esqueminha:
Repare que o momento fletor que achamos aponta no mesmo sentido que o nosso momento positivo, então ele é positivo:
Resposta
Exercício Resolvido #9
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 214, 5/130
Desenhe os diagramas de cortante e de momento para a viga em balanço carregada, para a qual o momento é ajustado de modo a produzir um momento nulo na extremidade engastada da viga. Determine o momento fletor em
Passo 1
Vamos primeiro calcular a força resultante do carregamento distribuído:
Então, temos o seguinte diagrama de corpo livre:
Repare que a força resultante fica localizada na metade do comprimento do carregamento distribuído, ou seja, a do engaste!
Vamos primeiro calcular a reação na parte engastada:
E quanto vale o momento Vamos fazer o somatório de momentos com relação ao engaste considerando o momento girando no sentido anti-horário como positivo:
Repare que não colocamos momento como reação no engaste, pois o enunciado disse que o momento deve ser nulo!!!
Passo 2
Agora vamos achar o cortante . Para isso vamos fazer uma seção em :
Para achar o cortante nesta seç��o, vamos fazer o somatório de forças verticais:
Ou seja, na parte que cortamos a viga o cortante é zero. Mas tem o cortante na parte inicial da viga devido à reação de apoio . Vamos analisar seu sinal:
Repare que o cortante é positivo, pois aponta no mesmo sentido do cortante positivo.
E o momento fletor ? Vamos usar o somatório de momentos com relação ao ponto :
Vamos analisar seu sinal:
Repare que o momento fletor é positivo!
Passo 3
Agora vamos analisar o que acontece no final da viga:
Para calcular o cortante é só fazermos o equilíbrio de forças:
Ou seja, o cortante continua sendo zero até o final da viga.
Como há um momento concentrado no final da viga, sabemos que vai ter uma descontinuidade do momento fletor. Então vamos analisar qual é o momento fletor um infinitésimo antes do momento :
Vamos fazer o somatório de momentos com relação ao ponto :
E o seu sinal será positivo, pois:
Agora vamos fazer uma seção um infinitésimo depois de do momento de modo a incluí-lo:
Esse momento fletor pode ser calculado pelo somatório de momentos com relação ao ponto de novo:
Ou seja, o momento fletor agora é zero!!!
Passo 4
Agora só falta uma coisinha... Lembra que o cortante é obtido integrando a equação do carregamento que estiver na viga e o momento fletor é obtido integrando a equação do cortante?
Como o carregamento é uma reta constante, o cortante vai ser uma reta que varia linearmente e o momento fletor vai ser uma parábola do segundo grau!
Sabemos que o cortante fica assim:
Vamos achar a equação desta reta. Sabemos que ela terá a seguinte forma:
Podemos calcular através da tangente do ângulo de inclinação da reta:
Mas repare que a reta está decrescendo, ou seja, o nosso será negativo:
Quando temos que , então:
Ou seja, a equação do cortante é:
Agora para achar a equação do momento fletor temos que integrar esta equação ao longo do comprimento da viga:
Agora sim podemos desenhar o diagrama do momento fletor:
Passo 5
Quando é só substituirmos o valor de nas equações de cortante e momento fletor que acabamos de achar:
E o momento fletor fica:
Resposta
Exercício Resolvido #10
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 215-5/136
Construa os diagramas de cortante e de momento para a viga carregada pelas cargas pontual e distribuída. Quais são os valores do cortante e do momento em ? Determine o momento fletor máximo .
Passo 1
Vamos começar fazendo o diagrama de corpo livre e como temos uma carga distribuída, vamos achar a resultante dela:
Agora podemos começar o equilíbrio calculando o momento com relação ao ponto :
E por fim o somatório de forças em cada eixo:
Passo 2
Onde tem reação de apoio tem descontinuidade do cortante, então nos pontos e o cortante vai de zero ao valor da reação:
Sendo que no ponto B, a reação aponta no sentido contrário do cortante positivo, então:
E o momento fletor nesses pontos? Como temos apoios que não impedem a rotação e estão na extremidade da viga sem nenhum momento concentrado sobre eles, então o momento nesses pontos é nulo:
Passo 3
Lembra que se temos a equação do cortante é só derivarmos para achar a equação do carregamento?
Só que não temos a expressão do cortante, pois é justamente o que queremos saber. Mas... temos o carregamento!!!
Nossa carga distribuída é retangular, logo a sua equação é uma constante e vale:
Para achar a equação do cortante a partir dessa equação é só integrarmos e multiplicar por , assim:
Lembra desse ? É a nossa constante de integração e temos que colocar toda vez que não temos um intervalo de integração definido.
Para acharmos seu valor, temos que saber quanto vale o cortante , ou seja, bem onde começa a carga distribuída, porque é fácil sabermos o cortante neste ponto.
Repare que do ponto até o ponto não há mais nenhuma força, então o cortante neste trecho é constante e vale o mesmo valor do cortante em pela direita.
Então, quando . Vamos substituir isto na fórmula de que achamos:
Então, a expressão do cortante para o trecho de carga distribuída é:
Passo 4
Então, quanto vale o cortante no ponto ? É só substituirmos o valor de :
Perceba que no trecho entre os pontos e não tem nada, então o cortante é constante neste trecho e com o valor de . Então, ao fazer uma seção no ponto :
Qual é a resultante do cortante neste ponto, então?
Passo 5
Lembra que derivando a equação do momento fletor obtemos a equação do cortante? Então, vamos fazer o processo inverso já que temos a expressão do cortante para o trecho .
Para achar o valor da constante temos que saber quanto vale o momento fletor em
, que é um ponto fácil de calcular:
Então, o momento fletor no ponto é:
Quando , vamos substituir isso na equação
Então, a equação do momento fletor no trecho é:
Passo 6
Para saber o momento fletor no ponto é só substituir na equação do momento:
Passo 7
Para calcular o momento fletor no ponto , é só vermos o momento que a reação e a força resultante faz com relação a este ponto:
Então, o momento fletor no ponto é :
Passo 8
O nosso diagrama do cortante, vai ficar:
O diagrama de momento fletor, vai ficar assim:
Passo 9
Feito os diagramas, podemos responder quais são os valores do cortante e do momento em
.
O cortante será:
Para sabermos o momento, vamos achar a equação da reta naquele trecho . Sabemos que é uma equação do primeiro grau da forma: e que quando:
Então nossa equação será:
Então, quando :
Passo 10
Para finalizar, vamos achar o momento máximo. Perceba que ele ocorre no trecho , então vamos derivar a equação do momento deste trecho e igualar à zero:
Sabemos que o momento máximo ocorre em , agora temos que achar o valor deste momento: