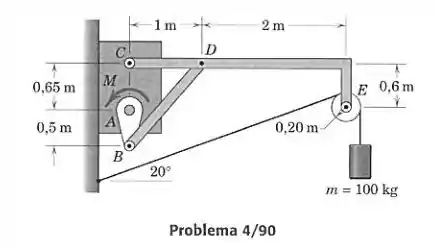
Quando a biela está na posição vertical, o eixo está na posição horizontal e o cabo faz um ângulo de 20° com a horizontal. Calcule o momento necessário para haver equilíbrio no suporte.
Passo 1
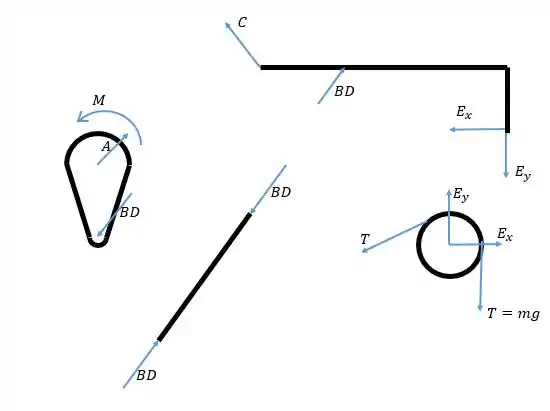
Vamos primeiro representar os corpos que estão envolvidos no problema em diagramas de corpo livre. Temos as barras e , a biela e a polia . Temos que prestar atenção em representar o sentido correto nas forças de ação e reação entre os corpos:
Passo 2
Queremos encontrar , e para isso vamos aplicar a soma dos momentos em relação a para a biela. Mas antes disso precisamos encontrar e para isso fazemos as equações de equilíbrio na barra em L. As forças e são encontradas primeiro através das o equilíbrio na polia. A força de tração no fio segura o corpo de 100 kg e então
Na polia:
Passo 3
Tendo e , podemos fazer para a barra o momento em relação a para encontrar . Precisamos do ângulo entre e a horizontal, e o encontramos da seguinte forma:
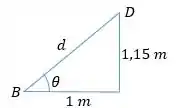
Agora fazemos o momento em relação a ser zero:
Substituindo os valores das forças de encontrados anteriormente e o :
Passo 4
Agora finalmente olhamos para a biela AB, e encontramos através do momento em torno de :