Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 95
Determine a força de aperto vertical em em termos da força aplicada ao cabo do rebitador, que mantém a peça em seu lugar.
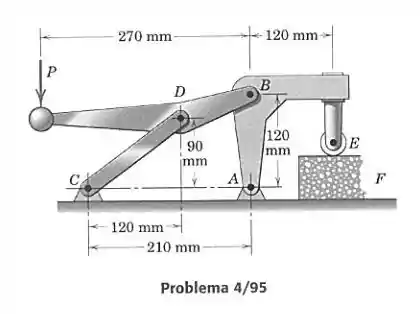
Passo 1
Quando a força é aplicada no cabo, a alavanca faz uma força em , e precisamos dessa força para utilizar nas equações de equilíbrio da parte e encontrar a força vertical em . Então vamos isolar as duas partes que tem contato com :
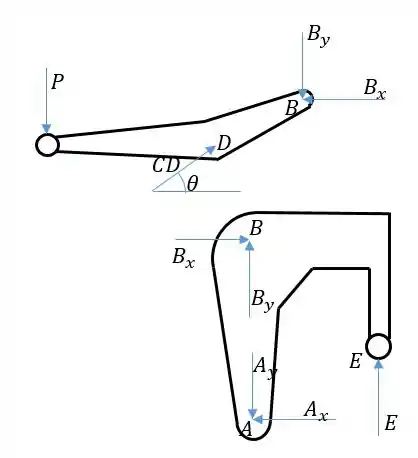
Passo 2
Olhando para o segundo corpo, percebemos que se fizermos o momento em torno de , conseguiremos achar a força só com o valor de , já que todas as outras forças tem linha de ação passando por . Então essa é a força que temos que achar no primeiro corpo. Vamos primeiro fazer o momento em torno de apara o primeiro corpo, pois assim achamos diretamente. Temos que saber o ângulo que a força faz com a horizontal:
A distância horizontal de a é mm e a distância vertical é mm:
Agora encontramos fazendo a soma das forças horizontais ser zero:
Passo 3
Agora igualando a zero o momento em torno de para o segundo corpo e usando o valor encontrado para , resolvemos achando :