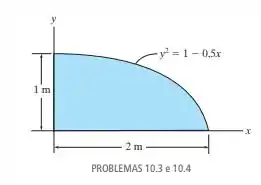
Determine o momento de inércia da área sombreada em relação ao eixo
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.
A fórmula geral para o momento de inércia de uma área em relação ao eixo é:
Onde:
é a distância do elemento de área ao eixo
é o elemento diferencial de área
Para calcular , é mais conveniente escolher um elemento de área horizontal (uma tira paralela ao eixo).
Passo 2
A equação da curva é dada por . precisamos isolar para usá-las em nossa integral em termos de .
Agora, substituímos e a expressão para na fórmula do momento de inércia:
Observando a figura, a área se estende de até m. Portanto, esses são nossos limites de integração.