Determine o produto de inércia do paralelogramo em relação aos eixos e .

Passo 1
Oi tudo bem? Vamos resolver este exercício.
Precisamos encontrar o produto de inercia em relação ao eixo e . Para isso, vamos considerar o seguinte desenho:
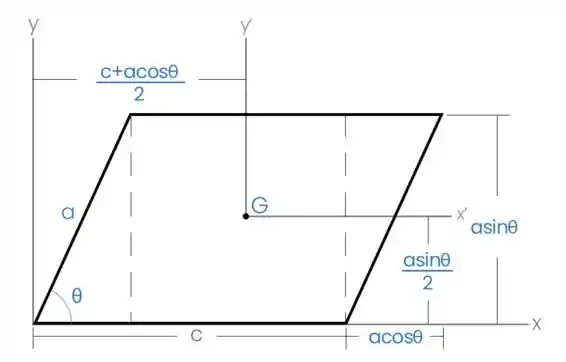
Vamos aos cálculos!
Passo 2
Nós iremos aplicar aqui o teorema dos eixos paralelos a todo o paralelogramo para determinar o seu produto de inercia sobre e . Mas antes disso precisaremos encontrar alguns valores primeiro.
Primeiro, nós iremos determinar o valor do produto de inercial do centroide de cada triangulo. Como esses triângulos que compõem a figura são iguais, então o produto será o mesmo.
Considere o triângulo mostrado abaixo:
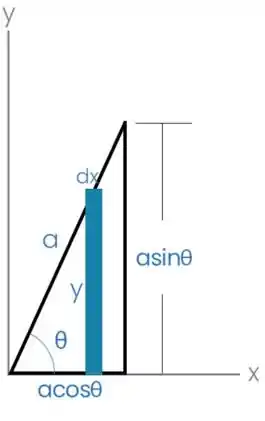
Passo 3
Nós iremos determinar primeiro determinando o produto de inercia sobre o eixo e . Nós iremos fazer isso aplicando o teorema dos eixos paralelos.
Passo 4
Agora nós podemos determinar integrando :
Agora nós podemos determinar aplicando o teorema do eixo paralelo. Dessa vez para todo o triangulo:
Passo 5
Agora iremos encontrar o produto de inercia de todo o paralelogramo em relação aos eixos e que passam através do centroide do paralelogramo. Utilizaremos novamente o teorema dos eixos paralelos:
Passo 6
Finalmente, agora podemos finalmente encontrar o que procurávamos desde o princípio: