Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 25

Determine as reações no elemento em “L” que é apoiado por uma superfície lisa em B e por uma luva em A , que está fixa ao elemento e livre para deslizar pela alça inclinada presa à parede.

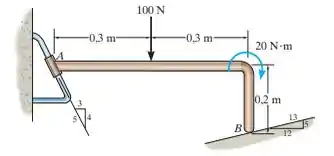
Passo 1

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Precisamos determinar as reações na luva em A (um momento M A e uma força perpendicular ao plano N A ) e na superfície lisa B (força perpendicular ao plano N B ).

Para isto, é fundamental fazermos um diagrama de corpo livre identificando as forças aos quais estão submetidos!!! Sempre que tiverem dúvida, voltem na Tabela 5.1 do livro! Lá são identificados os tipos de apoios com as suas reações!

Então, o nosso diagrama de forças será:

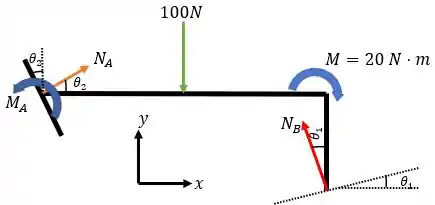
Sendo os ângulos θ 1 e θ 2 formados pelos planos inclinados (olhar a relação de triângulos que a questão descreve!).

Então, vamos as contas!

Passo 2

Vamos começar determinando as reações N A e N B . Para isto, vamos avaliar o equilíbrio das forças nas direções X e Y através do somatório das mesmas.

Sendo assim, temos:

∑ F x = 0 ∑ F y = 0 ⟹ N A ⋅ cos ⁡ θ 2 - N B ⋅ sen ⁡ θ 1 = 0 N A ⋅ sen ⁡ θ 2 + N B ⋅ cos ⁡ θ 1 - 100 = 0

Agora é só resolvermos o sistema acima. Relembrando, sen ⁡ θ 1 = 5 / 13 , cos ⁡ θ 1 = 12 / 13 , cos ⁡ θ 2 = 4 / 5 e sen ⁡ θ 2 = 3 / 5 . Desta forma, temos:

N A ⋅ 4 5 = N B ⋅ 5 13 N A ⋅ 3 5 + N B ⋅ 12 13 - 100 = 0

Resolvendo o sistema acima, obtemos N B = 82,5   N e N A = 39,7   N !

Passo 3

Para finalizarmos a questão, temos que descobrir qual o momento M A aplicado na luva A . Para isto, vamos fazer o somatório de momentos em relação ao ponto A . Portanto,

∑ M R A = 0

M A - 100 ⋅ 0,3 - M + N B ⋅ cos ⁡ θ 1 ⋅ 0,6 - N B ⋅ sen ⁡ θ 1 ⋅ 0,2 = 0

M A = 30 + 20 + 82,5 ⋅ 0,2 sen ⁡ θ 1 - 0,6 cos ⁡ θ 1

M A = 10,7   N ⋅ m

E assim finalizamos a questão!

Resposta

N A = 39,7   N

N B = 82,5   N

M A = 10,7   N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as reações externas em A e F para a treliça de um telhado carregada como mostrado. As cargas verticais representam o efeito de sustentação dos materiais do telhado, enquanto a força de 400N
O carro completo, com seu motorista, tem massa de 815k g e, sem os dois aerofólios, tem uma distribuição de peso igual ( 50 % - 50 % ) entre a dianteira e a traseira em uma dada velocidade na qual o c
O elemento O B C e a roldana em C , juntos, têm uma massa de 500k g , com um centro de massa combinado em G . Calcule o módulo da força suportada pela conexão de pino em O quando a carga de 3k N é apl
A porta de carga de um avião com fuselagem circular consiste de um segmento uniforme A B de um quarto de círculo e massa m . Uma trava na dobradiça em A mantém a porta aberta na posição mostrada. Dete
Determine a força trativa T no parafuso tensor do sistema polia-cabio em termos da massa m do corpo que ele sustenta. Despreze a massa das polias e do cabo.