Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.11 - Ex. 111

A figura mostra a vista lateral da estrutura das rodas (truque) de um vagão de passageiros onde a carga vertical é transmitida à estrutura em que os assentos dos mancais das rodas estão localizados. A vista inferior mostra apenas um par de rodas e seu eixo que gira com as rodas. Cada uma das rodas com 825   m m de diâmetro tem uma masssa de 250   k g , e o eixo de 315   k g tem um diâmetro de 125   m m . Se o trem está viajando a 130   k m / h enquanto contorna uma curva de 8 ° à direita (raio de curvatura 218   m ), calcule a variação ∆ R na força vertical suportada por cada roda devida apenas à ação giroscopica. Como uma boa aproximação, considere cada roda como um disco circular uniforme e o eixo como um cilindro maciço uniforme. Assuma também que ambos os trilhos estão no mesmo palno horizontal.

Vista Lateral do Truque

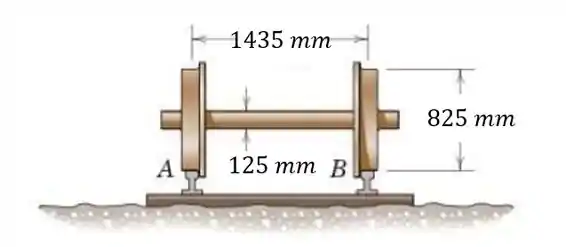
Vista das Rodas e do Eixo

Passo 1

Nota se que se trata de um movimento giroscópico ocorrendo em torno de um eixo normal as rodas então pode se aplica a seguinte equação.

M = I Ω × p = I ( - Ω i × p k )

M = I Ω p j

E o momento de inercia em torno do eixo de rotação das roda pode ser calculado por:

I Z Z = ∑ 1 / 2 m r 2

I Z Z = 2 1 2 250 ( 0,4125 2 ) + 1 2 315 ( 0,0625 2 )

I Z Z = 43,15   k g ∙ m 2

Passo 2

De acordo com o problema descrito, o seguinte esquema descritivo pode ser elaborado

p = v r = 130 / 3,6 0,4125 = 87,54   r a d / s

Ω = v ρ = 130 / 3,6 218 = 0,167   r a d / s

M = I Ω p j

M = ∆ R 1,435 = 43,15 * 87,54 * 0,167

∆ R = 436   N

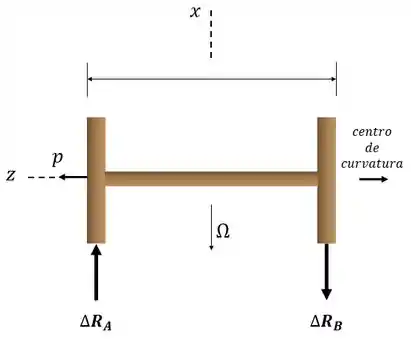
Resposta

A variação ∆ R na força vertical suportada por cada roda devida apenas à ação giroscopica é ∆ R = 436   N .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

114. O motor elétrico possui uma massa total de 10k g e é apoiado pelos suportes de montagem A e B presos a plataforma giratória. A armadura do motor possui uma massa de 2,5k g e um raio de giração de
115. A nave espacial apresentada é simétrica em relação a seu eixo z e possui um raio de giração de 720m m em relação a esse eixo. Os raios de giração em relação aos eixos x e y através do centro de m
122. Um projétil que se desloca através da atmosfera com uma velocidade v - que faz um pequeno ângulo θ com seu eixo geométrico é submetido a uma força aerodinâmica resultante R essencialmente no sent
123. O disco circular maciço de massa m e pequena espessura está girando livremente sobre seu eixo à taxa p . Se o conjunto é liberado na posição vertical em θ = 0 com θ ˙ = 0 , determine as component
106. As pás e o cubo do rotor do helicóptero têm uma massa de 64k g e um raio de giração de 3,0m em relação ao eixo de rotação z . Com o rotor girando a 500r p m durante um curto intervalo após a deco