Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 225

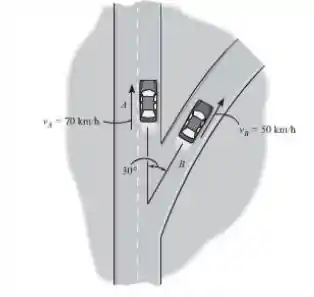
No instante mostrado, os carros A e B movem-se a velocidade de 70 Km/h e 50 Km/h, respectivamente. Se B está reduzindo sua velocidade escalar na razão de 1400 km/h2, determine a aceleração de B em relação a . O carro B move-se ao longo de uma curva tendo um raio de curvatura de 0,7 km.

Passo 1

Conforme o carro B descrever a trajetória curva em “desaceleração” , vetores de aceleração tangente e normal possuiem as seguintes orientações.

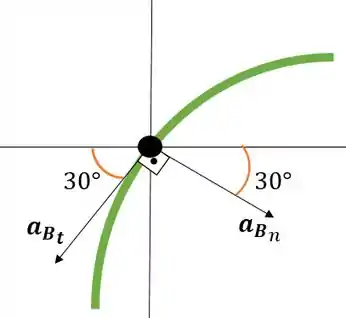
Passo 2

O modulo da aceleração normal pode ser calculado por

a B n = V B 2 ρ = 50 2 0,7 = 3371,43   k m / h 2

De acordo com direções, os vetores de aceleração normal e tangente do carro B, podem ser escritos sendo,

a B t = - 1400 sin ⁡ 30 ° i - 1400 cos ⁡ 30 ° j  

a B n = 3571,43 cos ⁡ 30 ° i - 3571,43 sin ⁡ 30 ° j

Passo 3

Para determinar a aceleração B em relação a A é necessário aplicar a seguinte equação, e carro A está com velocidade constante, portanto a aceleração é zero.

a B =   a A +   a B / A

- 1400 sin ⁡ 30 ° + 3571,43 cos ⁡ 30 ° i + - 1400 cos ⁡ 30 ° - 3571,43 sin ⁡ 30 ° j = 0 + a B / A

a B / A = 2692 , 95 i - 3798,15   j k m / h 2

o modulo da aceleração e a direção a B / A ,

a B / A =   2692 , 95 2 + ( - 3798,15 ) 2 = 4489   k m / h 2

ϕ =   tan - 1 ⁡ - 2478,54 2692,95 = 302,2 °

Resposta

A aceleração relativa é

a B / A = 2692 , 95 i - 3798,15   j k m / h 2

Sendo o modulo de 4489 km/h2 e a direção de 302,2 °   ou - 57,8 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carro está se deslocando a uma velocidade escalar constante de 100 km/h. Se a chuva está caindo a 6 m/s na direção mostrada, determine a velocidade da chuva tendo como referência o motorista.
O homem consegue remar o barco na água parada com uma velocidade escalar de 5 m/s. Se o rio esta fluindo a 2 m/s, determine a velocidade escalar do barco e o ângulo θ que ele deve direcionar o barco d
O navio move-se com uma velocidade escalar constante vs = 20 m/s e o vento está soprando a uma velocidade escalar vW = 10 m/s, como mostrado. Determine a intensidade e direção da componente horizontal
No instante mostrado, os carros A e B movem-se a velocidades escalares de 30 km/h e 20 km/h, respectivamente. Se B está aumentando a sua velocidade escalar na razão de 1200 km/h2, enquanto A mantém um
O carro B está se deslocando ao longo da estrada curva com uma velocidade escalar de 15 m/s enquanto reduz sua velocidade escalar 2 m/s2. Nesse mesmo instante, o carro C está se deslocando ao longo da