Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 46

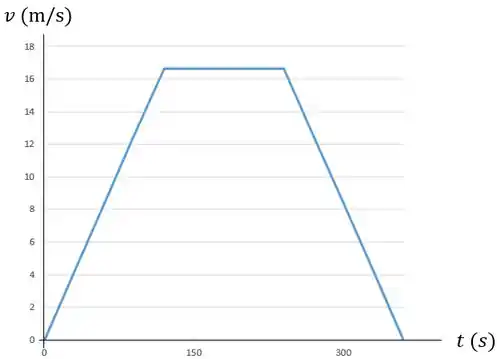
Um trem parte da estação A e no, percurso do primeiro quilômetro, ele move-se com aceleração uniforme. Então, pelos próximos 2 quilômetros, move-se com velocidade escalar uniforme. Por fim, o trem desacelera uniformemente por outro quilômetro antes de chegar ao repouso na estação B . Se o tempo para a jornada inteira é de 6 minutos, trace o gráfico v - t e determine a velocidade escalar máxima do trem.

Passo 1

A partir dos dados fornecidos pelo enunciado, podemos dividir a questão em três partes.

Momento 1:

Quando o trem parte da estação A e percorre s = 1 km com aceleração uniforme.

Momento 2:

O trem percorre s = 2 km e possui velocidade escalar uniforme. Logo, a = 0 .

Momento 3:

O trem percorre s = 1   km e desacelera uniformemente até chegar no ponto B , onde a velocidade v B = 0 .

O tempo total da jornada é de 6 minutos, ou seja

t t o t a l = 360   s

E o delocamento total será de

s 3 = 1000 + 2000 + 1000 = 4000   m

Devemos traçar o gráfico v - t e determinar a velocidade escalar máxima do trem v m á x .

Passo 2

Vamos começar analisando o Momento 1.

Este é o único trajeto em que o trem acelera, portanto sua velocidade máxima será atingida neste trecho.

Quando temos uma aceleração constante, utilizamos a seguinte equação para uma velocidade em função do tempo

v = v 0 + a t

Logo,

v m á x = 0 + a 1 t 1

Além disso, para uma aceleração constante, podemos escrever a velocidade como uma função da posição:

v 2 = v 0 2 + 2 a ∆ s

Logo,

v m á x 2 = 0 + 2 a 1 ( s 1 - s 0 )

v m á x 2 = 2 a 1 ( 1000 )

a 1 = v m á x 2 2000

Substituindo o valor de a 1 em v m á x , obtemos

v m á x = v m á x 2 2000 t 1

Logo,

t 1 = 2000 v m á x

Passo 3

No Momento 2, a velocidade é constante. Logo

v 2 = v m á x

Para encontrar o valor de t 2 deste trajeto, podemos utilizar a seguinte equação

s 2 = s 1 + v 1 t + 1 2 a t 2

Substituindo os valores conhecidos, obtemos

( 1000 + 2000 ) = 1000 + v m á x ( t 2 - t 1 ) + 0

t 2 - t 1 = 2000 v m á x

t 2 = 4000 v m á x

Passo 4

No Momento 3, o trem começa a desacelerar até atingir o repouso em t t o t a l = 360 s. Logo, t 3 = t t o t a l - t 2 .

Como a aceleração é constante, utilizamos a seguinte equação para uma velocidade em função do tempo

v = v 0 + a t

Logo,

0 = v m á x - a 3 t 3

v m á x = a 3 360 - t 2

Além disso, para uma aceleração constante, podemos escrever a velocidade como uma função da posição:

v 2 = v 0 2 + 2 a ∆ s

Logo,

0 = v m á x 2 - 2 a 3 ( 4000 - 3000 )

v m á x 2 = 2 a 3 ( 1000 )

a 3 = v m á x 2 2000

Substituindo o valor de a 3 em v m á x , obtemos

v m á x = v m á x 2 2000 360 - t 2

Logo,

t 2 = 360 - 2000 v m á x

Passo 5

Sabemos que

t 2 = 4000 v m á x

E que

t 2 = 360 - 2000 v m á x

Logo, igualando os valore de t 2 , obtemos

4000 v m á x = 360 - 2000 v m á x

4000 v m á x + 2000 v m á x = 360

6000 v m á x = 360

v m á x = 16,667   m / s

Passo 6

Agora vamos plotar o gráfico v - t .

No Momento 1:

t 1 = 2000 16,667 = 120   s

v 1 = v m á x 2 2000 t = 0,1389 t

No Momento 2:

t 2 = 4 000 16,667 = 240   s

No Momento 3:

t 3 = 360   s

v 3 = v m á x - v m á x 2 2000 t - 240

Logo, o gráfico é igual à:

Resposta

v m á x = 16 , 67   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A velocidade de uma partícula é dada por v = 25 t 2 - 80 t - 200 , onde v é em metros por segundo e t é em segundos. Represente graficamente a velocidade e a aceleração contra o tempo para os primeiro
Calcule a aceleração constante a em g s que a catapulta de um porta-aviões deve fornecer para produzir uma velocidade de lançamento de 300k m / h em uma distância de 100m . Suponha que o porta-aviões
A aceleração de uma partícula é dada por a ( t ) = 2 t - 10 , onde a é em metros por segundo ao quadrado e t é em segundos. Determine a velocidade e o deslocamento como funções do tempo. O deselocamen
A velocidade de uma partícula que se desloca ao longo do eixo s é dada por v = 2 - 4 t + 5 t 3 / 2 , onde t é em segundos e v é em metros por segundo. Calcule a posição s , a velocidade v , e a aceler
Uma bola é lançada verticalmente para cima com uma velocidade de 30m / s na borda de um penhasco com 60m . Calcule a altura h para a qual a bola se eleva e o tempo total t após a liberação para a bola