Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 47
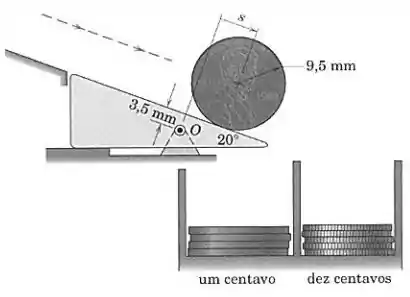
Parte de um separador mecânico de moedas funciona como se segue: Moedas de um e dez centavos rolam por um plano inclinado de , sendo que a parte triangular final do separador gira livremente em relação a um eixo horizontal passando por . As moedas de centavos são suficientemente leves ( gramas cada), de modo que a peça triangular permanece parada e as moedas rolam para a caixa de coleta à direita. As moedas de centavo, por outro lado, são suficientemente pesadas ( gramas cada), de forma que a peça triangular gira no sentido horário e as moedas caem na caixa de coleta à esquerda. Determine o momento em torno de , causado pelo peso de uma moeda de centavo em função da distância em milímetros.
Passo 1
Aqui, o momento em torno de será devido à força peso , para baixo. Então, podemos decompô-la em uma força paralela ao plano inclinado e uma força perpendicular ao plano, conforme mostra a figura a seguir:
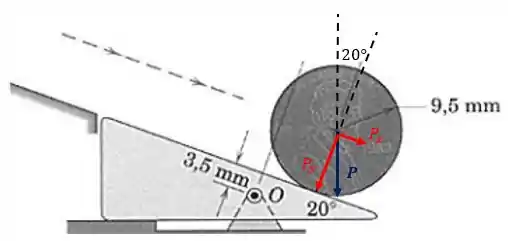
Em módulo, temos:
Passo 2
Pela figura, perceba que está agindo a uma distância “vertical” de do ponto e a uma distância “horizontal” , em milímetros. Ambas as forças agem para o sentido horário.
Então, calculamos o momento em torno de assim:
Resposta
(sentido horário)